Flujo Taylor-Couette
|
Read other articles:

Questa voce o sezione sull'argomento militari non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce sull'argomento gradi militari è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Un sottufficiale (NCO - Non-com...

Banyak spesies dari henbane membutuhkan vernalisasi sebelum berbunga. Vernalisasi (dari Bahasa Latin vernus, yang berarti ”Musim semi”) adalah induksi pada proses pembungaan tanaman dengan cara memberikan paparan dingin berkepanjangan atau dengan cara artifisial lain yang setara. Setelah vernalisasi tanaman akan mampu untuk berbunga namun tanaman mungkin membutuhkan seasonal cues tambahan atau mebutuhkan waktu beberapa minggu untuk tumbuh hingga akhirnya berbunga. Vernalisasi juga terkada...

Date MunenariDate Munenari Kepala UwajimaMasa jabatan1844–1858 PendahuluDate MunetadaPenggantiDate Mune'e Informasi pribadiLahir(1818-09-01)1 September 1818Edo, JepangMeninggal20 Desember 1892(1892-12-20) (umur 74)KebangsaanJepangSunting kotak info • L • B Ini adalah nama Jepang, nama keluarganya adalah Date. Marquis Date Munenari (伊達 宗城code: ja is deprecated , 1 September 1818 – 20 Desember 1892) adalah kepala Domain Uwajima kedelapan pada zaman keshogunan Toku...

Gavin McInnesMcInnes memandu acaranya pada Desember 2015Lahir1970 (umur 53–54)Hitchin, Hertfordshire, InggrisTempat tinggalLarchmont, New York, ASPekerjaanPenulis, komentator politikKota asalOttawa, Ontario, KanadaSuami/istriEmily Jendrisak (m. 2005)Anak3Situs webfreespeech.tv Gavin McInnes (/məˈkɪnɪs/; kelahiran 1970) adalah seorang penulis Inggris-Kanada dan komentator politik kanan jauh yang dikenal karena mempromosikan kekerasan ...

LanggikimaKelurahanNegara IndonesiaProvinsiSulawesi TenggaraKabupatenKonawe UtaraKecamatanLanggikimaKodepos93351Kode Kemendagri74.09.03.1003 Kode BPS7410060002 Luas-Jumlah penduduk-Kepadatan- Langgikima adalah kelurahan di kecamatan Langgikima, Kabupaten Konawe Utara, Sulawesi Tenggara, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administrasi Pemerintahan, dan Pulau tahun 2021 (Indonesia...

1976 film by Richard Lester The RitzThe theatrical release poster by Al Hirschfeld was used as one of the covers of its home video release.Directed byRichard LesterWritten byTerrence McNallyBased onThe Ritz1975 playby Terrence McNallyProduced byDenis O'DellStarring Jack Weston Rita Moreno Jerry Stiller Kaye Ballard F. Murray Abraham Paul B. Price Treat Williams CinematographyPaul WilsonEdited byJohn BloomMusic byKen ThorneDistributed byWarner Bros.Release date August 12, 1976 (...

Artikel ini bukan mengenai Xiangyang, Xingyang, atau Xinyang. Xianyang (Hanzi: 咸阳; Pinyin: Xiányáng) adalah sebuah kota tingkat prefektur di tengah provinsi Shaanxi, yang terletak di Sungai Wei yang berjarak beberapa kilometer dari ibukota provinsi Xi'an. Sempat menjadi ibukota dinasti Qin, kota tersebut sekarang terintegrasi ke kawasan metropolitan Xi'an. Referensi Bacaan tambahan Cotterell, Arthur (2007). The Imperial Capitals of China - An Inside View of the Celestial Empire....

إيهاب المساكني معلومات شخصية الميلاد 18 يوليو 1987 (العمر 36 سنة)تونس الطول 1.86 م (6 قدم 1 بوصة) مركز اللعب وسط الجنسية تونس أخوة وأخوات يوسف المساكني معلومات النادي النادي الحالي النجم الرياضي الساحلي الرقم 36 المسيرة الاحترافية1 سنوات فريق م. (هـ.) 2008–2012 الملعب �...

Contea di EctorconteaLocalizzazioneStato Stati Uniti Stato federato Texas AmministrazioneCapoluogoOdessa Data di istituzione1887 TerritorioCoordinatedel capoluogo31°52′12″N 102°32′24″W / 31.87°N 102.54°W31.87; -102.54 (Contea di Ector)Coordinate: 31°52′12″N 102°32′24″W / 31.87°N 102.54°W31.87; -102.54 (Contea di Ector) Superficie2 335 km² Abitanti137 130[1] (2010) Densità58,73 ab./km² Altre informa...

David Dastmalchian nel 2023 David Dastmalchian (Allentown, 21 luglio 1977) è un attore statunitense. Indice 1 Biografia 1.1 Vita privata 2 Filmografia 2.1 Attore 2.1.1 Cinema 2.1.2 Televisione 2.2 Doppiatore 2.3 Sceneggiatore 2.4 Produttore 3 Teatro 4 Doppiatori italiani 5 Note 6 Altri progetti 7 Collegamenti esterni Biografia Originario della Pennsylvania, Dastmalchian cresce a Overland Park, in Kansas.[1] Appassionatosi alla recitazione alle scuole superiori, frequenta la scuola di...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Waldshut district – news · newspapers · books · scholar · JSTOR (December 2015) (Learn how and when to remove this message) District in Baden-Württemberg, GermanyWaldshutDistrict FlagCoat of armsCountryGermanyStateBaden-WürttembergAdm. regionFreiburgCapi...

Dans ce nom coréen, le nom de famille, Lee, précède le nom personnel. Lee UfanRelatum par Lee Ufan (Bochum, 1978)Naissance 24 juin 1936 (87 ans)SéoulPériode d'activité 2002Nom dans la langue maternelle 이우환Pseudonyme Ufan, LeeNationalité sud-coréenneActivités Sculpteur, artiste graphique, pédagogue, écrivain, artiste visuel, graveur, créateur de bijoux, peintre, professeur d'universitéFormation Université NihonReprésenté par Pace Gallery (en), Lisson Gallery, Ga...
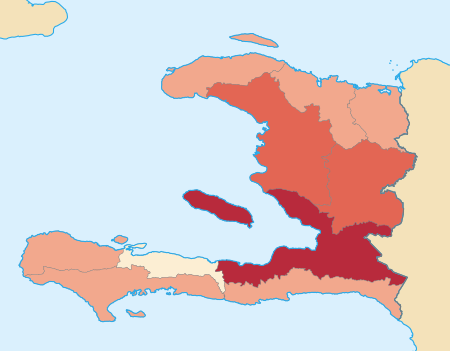
Pandemi COVID-19 di HaitiPenyakitCOVID-19Galur virusSARS-CoV-2LokasiHaitiKasus pertamaPort-au-PrinceTanggal kemunculan19 Maret 2020(4 tahun, 2 bulan, 3 minggu dan 5 hari)Kasus terkonfirmasi6.727[1]Kasus dirawat3.564[1]Kasus dicurigai‡15.146[1]Kasus sembuh3.022[1]Kematian141[1]Situs web resmihttps://mspp.gouv.ht‡ Kasus yang dicurigai belum dikonfirmasi karena galur ini sedang diteliti di laboratorium. Beberapa galur lain mungkin t...

South African footballer (1930–2007) Bill Perry Personal informationFull name William PerryDate of birth (1930-09-10)10 September 1930Place of birth Johannesburg, South AfricaDate of death 27 September 2007(2007-09-27) (aged 77)Position(s) Outside leftSenior career*Years Team Apps (Gls)1947–1949 Johannesburg Rangers ? (?)1949–1962 Blackpool 394 (119)1962–1963 Southport 26 (0)1963–1964 Hereford United 29 (0)1964–1965 South Coast United 1966–1967 Holyhead Town International c...

Questa voce o sezione sull'argomento centri abitati della Spagna non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. PozoamargocomunePozoamargo – Veduta LocalizzazioneStato Spagna Comunità autonoma Castiglia-La Mancia Provincia Cuenca TerritorioCoordinate39°22′00.12″N 2°12′00″W39°22...

MariaMaria seperti yang digambarkan di dalam Chronica HungarorumRatu Hungaria dan KroasiaBerkuasa1382–1385Penobatan17 September 1382PendahuluLajos IPenerusCarlo IIWaliElizabeta dari Bosnia Ratu Hungaria dan Kroasia bersama dgn Sigismund Berkuasa1386–1395PendahuluCarlo IIPenerusSigismundInformasi pribadiKelahiran1371Kematian17 May 1395 (umur 23–24)BudaPemakamanVárad (sekarang Oradea)WangsaWangsa Kapetia AnjouAyahLajos IIbuErzsébet dari BosniaPasanganSigismund Maria, (1371 ...

1994 studio album by PJ & DuncanPsycheStudio album by PJ & DuncanReleased4 November 1994 20 September 1995 (Japan)Recorded1993–94Genre pop rap teen pop Length43:02LabelTelstar RecordsProducer Nicky Graham Deni Lew Mike Olton PJ & Duncan chronology Psyche(1994) Top Katz(1995) Singles from Psyche Tonight I'm FreeReleased: 6 December 1993 Why Me?Released: 11 April 1994 Let's Get Ready to RhumbleReleased: 11 July 1994 If I Give You My NumberReleased: 26 September 1994 Etern...

2008 Ohio's 11th congressional district special election ← November 2008 November 18, 2008 2010 → Candidate Marcia Fudge Party Democratic Popular vote 8,450 Percentage 97.2% Representative before election Vacant Elected Representative Marcia Fudge Democratic Elections in Ohio Federal government U.S. President 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 1900 1904 1908 1912 1916 1920 1...

此條目需要补充更多来源。 (2013年2月11日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:霍奇克斯M1922輕機槍 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 霍奇克斯M1922 兩名正以霍奇克斯M1922輕機槍對空射擊的中國士兵类型�...

Radio station in Denver KBJDDenver, ColoradoFrequency1650 kHzBrandingRadio La REDProgrammingFormatSpanish ChristianOwnershipOwnerSalem Media Group(Salem Media of Colorado, Inc.)Sister stationsKNUS, KRKS, KRKS-FMTechnical information[1]Licensing authorityFCCFacility ID87151ClassBPower10,000 watts day1,000 watts nightTransmitter coordinates39°47′56″N 104°58′12″W / 39.79889°N 104.97000°W / 39.79889; -104.97000LinksPublic license information Public file...




















