Aproximación diofántica
|
Read other articles:

Synthetic and orally active anabolic–androgenic steroid (AAS)TetrahydrogestrinoneClinical dataOther namesTHG; The Clear; 17α-Ethyl-18-methyl-δ9,11-19-nortestosterone; 17α-Ethyl-18-methylestra-4,9,11-trien-17β-ol-3-oneRoutes ofadministrationBy mouth, intramuscular injectionDrug classAndrogen; Anabolic steroid; ProgestogenLegal statusLegal status US: Schedule III Identifiers IUPAC name (8S,13S,14S,17S)-13,17-diethyl-17-hydroxy-1,2,6,7,8,14,15,16-octahydrocyclopenta[a]phenanthren-3-on...

Collection of businesses in the Inner Harbor section of Baltimore, Maryland, US This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Power Plant Live! – news · newspapers · books · scholar · JSTOR (October 2016) (Learn how and when to remove this template message) 39°17′21.7″N 76°36′24.8″W / 39.289361°N ...

Japan's political system This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Emperor system – news · newspapers · books · scholar · JSTOR (March 2024) (Learn how and when to remove this template message) Part of the Politics seriesMonarchy Central concepts MonarchMonarchismDivine right of kingsMandate of HeavenR...

King in Hindu tradition PururavasAn illustration of PururavasOther namesPurūravāTextsMahabharata, Rigveda, Vikramōrvaśīyam, PuranasGenderMalePersonal informationParentsIlā (mother)Budha (father)SpouseUrvashiChildrenAyus, Amavasu, Vishvayu or Vanayus, Shrutayu or Dhimat, Shatayu (or Satayu), and DridhayuDynastyChandravamsha Pururavas (Sanskrit: पुरूरवस्, Purūravas) is a character in Hindu literature, a king who served as the first of the Lunar dynasty.[1] Accord...
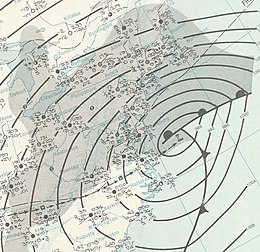
Early-season winter storm that impacted the Mid-Atlantic and New England of the United States December 1960 nor'easterCategory 2 Significant (RSI/NOAA: 5.79)A surface weather analysis of the intensifying nor'easter on December 12: click to enlarge Typenor'easterFormedDecember 10, 1960DissipatedAfter December 14, 1960 Lowest pressure966 millibars Maximum snowfallor ice accretion21.4 inches (54 cm)[1] Fatalities~286Areas affectedMidwestern United States, Mid...
ZFP91 التراكيب المتوفرة بنك بيانات البروتينOrtholog search: PDBe RCSB قائمة رموز معرفات بنك بيانات البروتين 2M9A المعرفات الأسماء المستعارة ZFP91, DMS-8, DSM-8, PZF, ZFP-91, ZNF757, FKSG11, zinc finger protein, zinc finger protein, atypical E3 ubiquitin ligase, DSM8 معرفات خارجية MGI: MGI:104854 HomoloGene: 43144 GeneCards: 80829 علم الوجود الجيني الوظيفة الجزيئي�...

Pacifica Radio station in New York City This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: WBAI – news · newspapers · books · scholar · JSTOR (August 2020) (L...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2022)Learn how and when to remove this message ألفريد فور الاسم الرسمي (بالفرنسية: base Alfred-Faure) الإحداثيات 46°25′56″S 51°51′30″E / 46.4323°S 51.8582°E / -46.4323; 51.8582 تاري...

映画については「私刑 リンチ」をご覧ください。 殺人 殺人 暗殺 王殺し 快楽殺人 拡大自殺 カニバリズム 拷問殺人 私刑 ジェノサイド ジェンダーサイド (アンドロサイド フェミサイド) シリアルキラー(ヘルスケア・シリアルキラー) スプリー・キラー 大量殺人 同士討ち 乗物による突入攻撃 人身御供 放伐 民衆殺戮 名誉の殺人 法域によっては犯罪でない殺人 安楽死 �...

ألفية: ألفية 3 قرون: القرن 20 – القرن 21 – القرن 22 عقود: عقد 1990 عقد 2000 عقد 2010 – عقد 2020 – عقد 2030 عقد 2040 عقد 2050 سنين: 2017 2018 2019 – 2020 – 2021 2022 2023 سنة 2020 (بالأرقام الرومانية: MMXX) هي سنة كبيسة بدأت يوم الأربعاء (الرابط يظهر نموذج الجدول الزمني الكامل للسنة) م�...

Earthquakes (6.0+ Mw) between 1900 and 2017 Earthquakes are caused by movements within the Earth's crust and uppermost mantle. They range from weak events detectable only by seismometers, to sudden and violent events lasting many minutes which have caused some of the greatest disasters in human history. Below, earthquakes are listed by period, region or country, year, magnitude, cost, fatalities and number of scientific studies. Lists by time period By century Before 1901 1901–2000 2001–...

Air mata pengantin Antigonon leptopus Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Eudikotil inti Ordo: Caryophyllales Famili: Polygonaceae Genus: AntigononEndl.[1] Spesies lihat teks Sinonim Corculum Stuntz[1] Air mata pengantin (Antigonon) adalah tumbuhan memanjat (liana) anggota suku Polygonaceae yang berasal dari Amerika Tengah. Dengan dua atau tiga jenis anggota, tumbuhan ini adal...

1958 studio album by Carl SmithLet's Live a LittleStudio album by Carl SmithReleased1958GenreCountryLabelColumbia Records Let's Live a Little is a studio album by country music singer Carl Smith. It was released in 1958 by Columbia Records (catalog no. CL-1172). In Billboard magazine's annual poll of country and western disc jockeys, it was ranked No. 14 among the Favorite Country Music LPs of 1958.[1] AllMusic gave the album a rating of four stars.[2] Track listing Si...

林文慶个人资料性别男出生1869年10月18日海峡殖民地檳城逝世1957年1月1日(1957歲—01—01)(87歲) 英属新加坡政党無黨籍配偶黃端瓊(Margaret Huang Tuan Keng)(1896年结婚—1905年丧偶)殷碧霞(Grace Yin Pek Ha)(1908年结婚—1957年結束) 学历 英國愛丁堡大學醫學院內科學士 英國愛丁堡大學醫學院外科碩士 1929.02- 香港大學名譽法學博士學位 经历 新嘉坡中國女學堂創辦人 1899- 爪哇�...

Avenue in Brooklyn and Queens, New York This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Grand Street and Grand Avenue – news · newspapers · books · scholar · JSTOR (January 2007) (Learn how and when to remove this message) Grand StreetGrand AvenueThe Grand Street Bridge over the Newtown Creek, as seen from B...

File:Kelebek.gif This is a Wikipedia user talk page.This is not an encyclopedia article or the talk page for an encyclopedia article. If you find this page on any site other than Wikipedia, you are viewing a mirror site. Be aware that the page may be outdated and that the user whom this page is about may have no personal affiliation with any site other than Wikipedia. The original talk page is located at https://en.wikipedia.org/wiki/User_talk:7%266%3Dthirteen. Beware! This user's talk page i...

Gran Premio di Magny-Cours 2015 Prova del mondiale SuperbikeProva 12 su 13 del 2015 Data 4 ottobre 2015 Nome ufficiale Fassi French Round Luogo Magny-Cours Percorso 4,411 km Risultati Superbike gara 1 691ª gara nella storia del campionato Distanza 19 giri, totale 83,809 km Pole position Giro più veloce Leon Haslam Jonathan Rea Aprilia in 1'56.404 Kawasaki in 1'53.247 (nel giro 16 di 19) Podio 1. Jonathan ReaKawasaki 2. Tom SykesKawasaki 3. Sylvain GuintoliHonda Superbike gara 2 6...

Pour les articles homonymes, voir Greyhound. Greyhound Lines Création 1914 Dates clés 2007 : Rachat par First Group 2021 : Rachat par FlixBus Fondateurs Carl Éric Wickman Forme juridique Corporation (d) Slogan Nous passons sur votre route Siège social Dallas, Texas États-Unis Direction Dave Leach Activité Transporteur Société mère Flix Filiales Greyhound Courrier ExpressGray LineBoltbus (low-cost) Effectif 8 400 Site web www.greyhound.com Société précédente S...
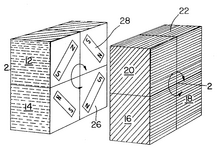
American puzzle designer Larry D. NicholsBornLarry Nichols1939 (age 84–85)Xenia, OhioNationalityAmericanEducationDePauw University; Harvard Graduate SchoolOccupation(s)Inventor, chemistEmployer(s)Moleculon Research Corporation of Cambridge, MassachusettsKnown forPuzzle designer, inventorTitleChief scientist Diagram from Nichols' patent showing a cube held together with magnets Pocket Cube animation. Larry D. Nichols, born 1939 in the United States, is a puzzle designer. He gre...







![{\displaystyle [2;1,2,1,1,4,1,1,6,1,1,8,1,\ldots \;].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c259691dfec787fa250436b39b9a345df73ea01d)














