Jakobia matrico
|
Read other articles:

Disambiguazione – Se stai cercando l'omonimo film per la televisione del 1996, vedi Doctor Who (film). Doctor WhoIl logo della serie dal 2022Titolo originaleDoctor Who PaeseRegno Unito Anno1963-1989 (serie classica)1996 (film TV)2005 - 2022 (serie revival) 2023 - in produzione (nuova serie) Formatoserie TV Generefantascienza, avventura, fantastico, drammatico Stagioni26 (serie classica)1 film TV13 (nuova serie) Episodi697 (serie classica)172 (nuova serie) Durata25 min (1963-198...

Distrik Denguélé District du DenguéléDistrikNegara Pantai GadingDibentuk2011Ibu kotaOdiennéLuas[1] • Total20.900 km2 (8,100 sq mi)Populasi (2021)[2] • Total436.015 • Kepadatan21/km2 (54/sq mi) Distrik Denguélé (Prancis: district du Denguélécode: fr is deprecated , [distʁikt dy dɛnɡele]) adalah salah satu dari empat belas distrik administratif di Pantai Gading. Distrik ini terletak di sudut barat laut...
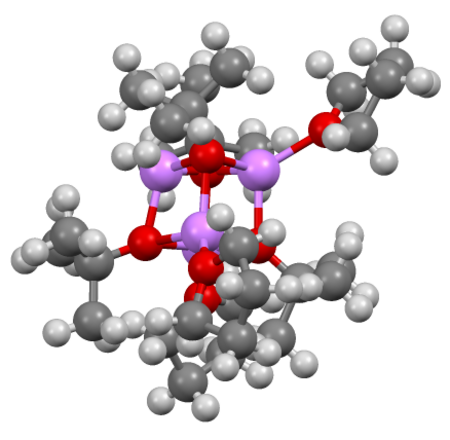
Struktur anion metoksida. Meskipun alkoksida logam alkali bukan termasuk garam dan memiliki struktur yang kompleks, secara kimiawi, mereka bertindak sebagai sumber RO−. Alkoksida adalah sebuah basa konjugat dari suatu alkohol sehingga mengandung gugus organik yang terikat pada atom oksigen yang bermuatan negatif. Alkoksida ditulis sebagai RO−, dengan R adalah substituen organik. Alkoksida adalah basa kuat dan, jika R tidak besar, merupakan nukleofil yang baik serta ligan yang bagus. Meski...

العلاقات السريلانكية المدغشقرية سريلانكا مدغشقر سريلانكا مدغشقر تعديل مصدري - تعديل العلاقات السريلانكية المدغشقرية هي العلاقات الثنائية التي تجمع بين سريلانكا ومدغشقر.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين:...
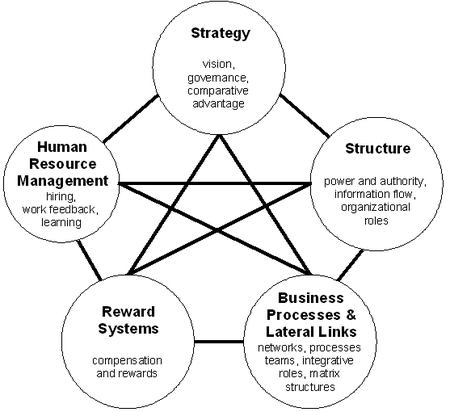
Procedural structure of an organization Business administration Management of a business Accounting Management accounting Financial accounting Audit Business entities Corporate group Conglomerate (company) Holding company Cooperative Corporation Joint-stock company Limited liability company Partnership Privately held company Sole proprietorship State-owned enterprise Corporate governance Annual general meeting Board of directors Supervisory board Advisory board Audit committee Corporate law C...

Sculpture in Hyde Park, Sydney, Australia 'Yininmadyemi' - Thou didst let fallArtistTony AlbertYear2015TypeSculptureLocationHyde Park, Sydney, AustraliaCoordinates33°52′30.7″S 151°12′35.9″E / 33.875194°S 151.209972°E / -33.875194; 151.209972 Yininmadyemi - Thou didst let fall is a sculptural artwork by Indigenous Australian artist Tony Albert located in Hyde Park, Sydney. Unveiled on 31 March 2015, the artwork acknowledges the service of Aboriginal and Torr...
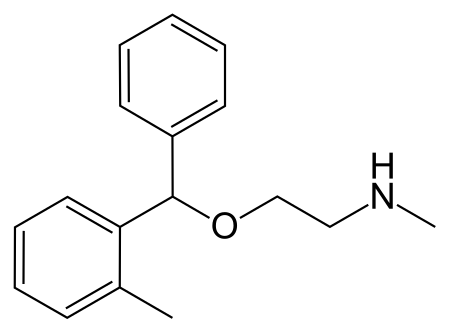
SNRI antidepressant medication TofenacinClinical dataTrade namesElamol, Tofacine, TofalinOther namestofenacin hydrochloride (USAN US)Routes ofadministrationBy mouthATC codeNoneLegal statusLegal status In general: ℞ (Prescription only) Identifiers IUPAC name N-methyl-2-[(2-methylphenyl)(phenyl)methoxy]ethanamine CAS Number15301-93-6 10488-36-5 (HCl)PubChem CID25315ChemSpider23647UNIIC4A112M10HECHA InfoCard100.035.746 Chemical and physical dataFormulaC17H21NOMolar mass255.361 g...

2016 studio album by Buddy GoodeMore RubbishStudio album by Buddy GoodeReleased16 December 2016Length29:04LabelGoode Times Music, ABC MusicBuddy Goode chronology Songs to Ruin Every Occasion(2015) More Rubbish(2016) More Rubbish is the sixth studio album by Michael Carr's comedy character Buddy Goode. It was released on 16 December 2016 both digitally and on CD.[1] The album was launched at the Rooty Hill RSL on 17 December 2016.[2] On 4 October 2017, it was announced...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Territoire d'application de l'article 7 : États membres de la Convention EDH. L'article 7 de la Convention européenne des droits de l'homme[1] intitulé « Pas de peine sans loi », est relatif à la non-rétroactivité de la loi pénale, version plus complète de l'expression « nullum crimen, nulla poena sine lege » ou principe de légalité. Disposition « Article 7 - Pas de peine sans loi Nul ne peut être condamné pour une action ou une omission qui, au ...

Polygon with an infinite number of sides For the novel, see Apeirogon (novel). The regular apeirogonEdges and vertices∞Schläfli symbol{∞}Coxeter–Dynkin diagramsInternal angle (degrees)180°Dual polygonSelf-dual A partition of the Euclidean line into infinitely many equal-length segments can be understood as a regular apeirogon. In geometry, an apeirogon (from Ancient Greek ἄπειρος apeiros 'infinite, boundless', and γωνία gonia 'angle') or infini...

Metropolis Pt. 2: Scenes from a MemoryDesain sampul oleh Dave McKeanAlbum studio karya Dream TheaterDirilis26 Oktober 1999 (1999-10-26)[1]GenreProgressive metal, progressive rockDurasi77:06LabelElektraProduserMike Portnoy, John PetrucciKronologi Dream Theater Once in a LIVEtime(1998)Once in a LIVEtime1998 Metropolis Pt. 2: Scenes from a Memory(1999) Live Scenes from New York(2001)Live Scenes from New York2001 Singel dalam album Metropolis Pt. 2: Scenes from a Memory Home (pro...

Cinema ofFrance 1892–1909 1910s 1910 1911 1912 1913 19141915 1916 1917 1918 1919 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 19841985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 19...

قائمة بمدن ولاية نيويورك في الولايات المتحدة ويبلغ عددها 62 مدينة: موقع ولاية نيويورك في الولايات المتحدة ألباني، نيويورك، عاصمة ولاية نيويورك بينغامتون، نيويورك بوفالو، نيويورك روتشستر سيراكيوز، نيويورك نيويورك، أكبر مدينة في ولاية نيويورك والولايات المتحدة نياجارا فو...

Final Piala Super Spanyol 2023TurnamenPiala Super Spanyol 2022–2023 Real Madrid Barcelona 1 3 Tanggal15 Januari 2023 (2023-01-15)StadionStadion Internasional Raja Fahd, RiyadhPemain Terbaik Gavi (Barcelona)[1]WasitRicardo de Burgos Bengoetxea (País Vasco)[2]Penonton57.340[3]CuacaCerah14 °C (57 °F)88% kelembapan[4]← 2022 2024 → Final Piala Super Spanyol 2023 menentukan juara Piala Super Spanyol 2022–2023, edisi ke-39 dari kompet...

Dance in the RainLagu oleh Koda Kumidari album Walk of My LifeDirilisNovember 5, 2014FormatSingel Digital, CD+DVD (hanya klub penggemar)Direkam2014GenreR&B, dansaDurasi6:37LabelRhythm ZonePenciptaKoda Kumi, her0ism • Ziggy • Melanie FontanaProduserMasaki Yokobe Dance In The Rain adalah sebuah singel R&B/pop karya penyanyi-penulis lagu Jepang Kumi Koda. Karya tersebut dirilis luas sebagai singel digital dan hanya dirilis secara fisik di kalangan klub penggemar resminya.[1]&...

HSBC Tower 旧名称 CN Tower Building概要所在地 Canary Wharf, London Borough of Tower Hamlets着工 1997完成 2002高さ屋上 200メートル (656 ft)技術的詳細階数 45設計・建設建築家 フォスター・アンド・パートナーズテンプレートを表示 エイト・カナダ・スクウェア(8 Canada Square)は、イギリス・ロンドンの再開発地・カナリー・ワーフにある超高層ビル。「HSBCタワー」とも言う。 概要 HSBCホ�...

Аниса Ахмед Дата рождения 29 сентября 1949(1949-09-29) (74 года) Страна Мальдивы Род деятельности активистка за права женщин, политик Награды и премии Международная женская премия за отвагу (2012) Медиафайлы на Викискладе Аниса Ахмед — мальдивская активистка за пра...

Die Ruinen von Persepolis, Residenzstadt des persischen Achämenidenreichs Altertum ist ein Begriff der Geschichtswissenschaft. Für die mediterran-vorderasiatischen Zivilisationen umfasst er den Zeitraum vom Ende der Urgeschichte (bis Mitte 4. Jahrtausend v. Chr.) bis zum beginnenden Mittelalter (ab 6. Jahrhundert). Räumlich bezieht er sich auf den Mittelmeerraum und Vorderasien. Das Altertum umfasst die klassische Antike sowohl zeitlich (je nach Abgrenzung ab dem 17./16., 11. oder 8. Jahrh...

Humbert of MaroillesAbbotBornin early 7thMézières-sur-OiseDied~682Venerated inEastern Orthodox ChurchRoman Catholic ChurchFeast25 MarchAttributesA star on his forehead; a bear carrying Humbert's baggage; with an angel making a cross on Humbert's brow; with an angel showing Humbert the Cross[1]PatronageOttawa, Canada Humbert of Maroilles Humbert of Maroilles (died ca. 680) was a Frankish monk, abbot, and saint. He founded Maroilles Abbey. Life Humbert was born at Mézières-sur-...











