|
7-hiperkuba kahelaro
| 7-hiperkuba kahelaro
|
| Speco
|
Regula 7-dimensia kahelaro
Hiperkuba kahelaro
|
| Vertica figuro
|
7-kruco-hiperpluredro
(128 7-hiperkuboj {4,3,3,3,3,3} ĉirkaŭ ĉiu vertico)
|
| Simbolo de Schläfli
|
{4,3,3,3,3,3,4}
|
| Figuro de Coxeter-Dynkin
|
![]()              
 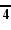           
|
| Edroj
|
Kvadratoj {4}
|
| Ĉeloj
|
Kuboj {4,3}
|
| 4-hiperĉeloj
|
4-hiperkuboj {4,3,3}
|
| 5-hiperĉeloj
|
5-hiperkuboj {4,3,3,3}
|
| 6-hiperĉeloj
|
6-hiperkuboj {4,3,3,3,3}
|
| 7-hiperĉeloj
|
7-hiperkuboj {4,3,3,3,3,3}
|
| Geometria simetria grupo
|
[4,3,3,3,3,3,4]
|
| Propraĵoj
|
Vertico-transitiva, latero-transitiva, edro-transitiva, ĉelo-transitiva
|
| Duala
|
Mem-duala
|
|
En geometrio, la 7-hiperkuba kahelaro estas la sola regula kahelaro de la eŭklida 7-spaco.
Ĝi estas analogo de la kvadrata kahelaro de la ebeno kaj de la kuba kahelaro de la 3-spaco.
Vidu ankaŭ
Referencoj
- H. S. M. Coxeter, Regular Polytopes - Regulaj hiperpluredroj, 3-a. red., Dover Publications, 1973. ISBN 0-486-61480-8, p.296, Tabelo II: Regulaj kahelaroj
|
|