Translation (geometry)
|
Read other articles:

Abdur Rahman Biswasআবদুর রহমান বিশ্বাস Presiden BangladeshMasa jabatan10 Oktober 1991 – 9 Oktober 1996Perdana MenteriKhaleda ZiaMuhammad Habibur Rahman (sementara)Sheikh Hasina PendahuluShahabuddin Ahmed (sementara)PenggantiShahabuddin Ahmed Informasi pribadiLahir(1926-09-01)1 September 1926Shaistabad, Distrik Barisal, Kepresidenan Benggala, India Britania[1]Meninggal3 November 2017(2017-11-03) (umur 91)Dhaka, BangladeshMakamBanani gra...

BlambanganDesaKantor Desa BlambanganPeta lokasi Desa BlambanganNegara IndonesiaProvinsiJawa TimurKabupatenBanyuwangiKecamatanMuncarKode pos68472Kode Kemendagri35.10.05.2005 Luas7.06 km²Jumlah penduduk7,615 jiwaKepadatan1,078.61 jiwa/km² Blambangan adalah sebuah desa di Kecamatan Muncar, Kabupaten Banyuwangi, Jawa Timur, Indonesia. Pembagian wilayah Desa ini terdiri dari 3 dusun, yaitu: Dusun Krajan Dusun Mangunrejo Dusun Sukosari lbsKecamatan Muncar, Kabupaten Banyuwangi, Jawa TimurDes...

Nicola Stefanini Informazioni personali Arbitro di Calcio Sezione Prato Professione Consulente Attività nazionale Anni Campionato Ruolo 2004-20052005-2011 Serie BSerie A e B ArbitroArbitro Premi Anno Premio 2014 Arbitro benemerito Nicola Stefanini (Firenze, 22 gennaio 1975) è un ex arbitro di calcio italiano. In tutte le partite dirette da lui in Serie A, una sola volta c'è stata una vittoria esterna.[1] Carriera Stefanini viene dalla sezione di Prato. Dopo aver totalizzato 37 pre...

American cyber-themed action-adventure television series IntelligenceGenre Action/Adventure Drama Espionage Science fiction Created byMichael SeitzmanDeveloped byMichael SeitzmanTripp VinsonStarring Josh Holloway Meghan Ory Michael Rady John Billingsley P. J. Byrne Marg Helgenberger Theme music composerClinton ShorterComposerClinton ShorterCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes13ProductionExecutive producers Michael Seitzman Tripp Vinson Barry Sch...

هذه المقالة عن بغداد عاصمة جمهورية العراق. لمعانٍ أخرى، طالع بغداد (توضيح). بَغْدَاد منَ الأعلى باتِجاه عَقارب الساعة: نَهر دِجلة، بُرج بَغداد، المٌتحَف العِراقي، نَصب الحُرية، القَصر العَباسي، نَصب الشَهيد، نَصب إنقاذ الثَقافة، الحَضرة الكاظِمية، الحَضرة الحَنَف...

Isole dei PoveriGeografia fisicaLocalizzazionemar Tirreno Coordinate41°05′N 9°34′E / 41.083333°N 9.566667°E41.083333; 9.566667Coordinate: 41°05′N 9°34′E / 41.083333°N 9.566667°E41.083333; 9.566667 ArcipelagoArcipelago di La Maddalena Geografia politicaStato Italia Regione Sardegna Provincia Sassari CartografiaIsole dei Poveri voci di isole d'Italia presenti su Wikipedia Le isole dei Poveri sono un gruppo di isolotti del mar...

Komite SentralPartai Komunis Uni Soviet Центральный комитет КПССTsentralniy Komitet KPSSJenisJenisKomite Sentral dari Partai Komunis Uni Soviet PimpinanPemimpinSekretaris Jenderal Dipilih olehKongres Partai Komunis Bertanggung jawab kepadaKongres Partai Komunis Bertanggung jawab atasKomisi Komite Pusat, Departemen Komite Pusat, Politbiro, Orgbiro, Sekretariat, dan lembaga negara pada umumnya AnggotaBervariasiTempat bersidangLapangan Staraya, Moskwa, RSFS Rusia L •...

Simulation video game 1997 video gameKlondike MoonCover Art for Luna TicksDeveloper(s)TerraForm SoftwarePublisher(s)21st Century EntertainmentManaccomPlatform(s)Windows 95, DOSRelease1997Genre(s)SimulationMode(s)Single player, Multiplayer Klondike Moon is a 1997 simulation video game for Windows 95 and DOS developed by TerraForm Software and published by 21st Century Entertainment. The game was distributed in the same year as Luna Ticks in Australia and New Zealand by Australian publisher Man...

Lists of Italian films 1910s 1910 1911 1912 1913 19141915 1916 1917 1918 1919 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 19841985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 1994199...

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1]...
British cable television channel Home Video Channel (HVC) was a British cable television channel that began operating in 1985, broadcasting low-budget films between 8:00 p.m. and midnight. Film genres included horror, action, adventure, science fiction, and erotica. In 1992, a second channel, The Adult Channel, was launched by HVC's owner, Home Video Channel Limited (HVCL). It broadcast erotic films and softcore pornography. In 1994, HVCL was acquired by Spice Networks, a television chan...

U.S. military tribunals Court room where initial Guantanamo military commissions convened. The Guantanamo military commissions were established by President George W. Bush through a military order on November 13, 2001, to try certain non-citizen terrorism suspects at the Guantanamo Bay prison.[1] To date, there have been a total of eight convictions in the military commissions, six through plea agreements. Several of the eight convictions have been overturned in whole or in part on ap...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) An editor has performed a search and found that sufficient sources exist to establish the subject's notability. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bangladeshis in Saudi Arabia – news · newspapers · books · ...
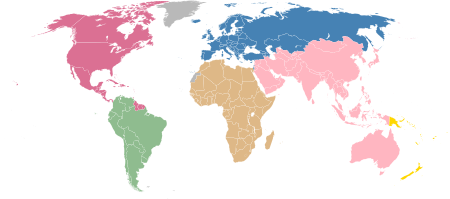
The World Leagues Forum (WLF) is an organization representing professional association football leagues that formed in 2016. It currently includes 44 members from five of FIFA's six continental confederations. History Executives and representatives from 24 professional football leagues convened the Global Leagues Forum in April 2015 to discuss current issues with the football system and business as a whole.[1] The World Leagues Forum was formed in early 2016 in preparation for the 20...

Brasileirão 2015 Généralités Sport Football Organisateur(s) CBF Édition 59e Lieu(x) Brésil Date 9 mai 2015 au 6 décembre 2015 Participants 20 équipes Site web officiel CBF - Brasileiro Série A Hiérarchie Hiérarchie 1er niveau Niveau inférieur Série B Palmarès Tenant du titre Cruzeiro EC Promu(s) en début de saison Joinville ECPonte PretaVasco da GamaAvaí Navigation Série A 2014 Série A 2016 modifier La saison 2015 de Série A, officiellement appelée Brasileirão Chevr...

ProfesorLászló LovászLászló Lovász berpidato pada 2007 di EPFLLahirLovász László09 Maret 1948 (umur 76)Budapest, Republik HungariaKebangsaanHungaria, Amerika SerikatAlmamaterUniversitas Eötvös LorándAkademi Sains HungariaPenghargaanAbel Prize (2021) Kyoto Prize in Basic Sciences (2010)John von Neumann Theory Prize (2006)Gödel Prize (2001)Knuth Prize (1999)Wolf Prize (1999)Fulkerson Prize (1982)Pólya Prize (SIAM) (1979)Karier ilmiahBidangMatematika, Ilmu komputerInstitusiUn...

Okayama International CircuitLokasiMimasaka, Okayama Prefecture, JapanZona waktuGMT +9Acara besarSuper GTMFJ SuperbikeSuper TaikyuWTCC (former)[1]F1 Pacific Grand Prix (former)Panjang3.703 km (2.300 mi)Tikungan13Rekor lap1:14.023 ( Michael Schumacher, Benetton B194, 1994)Situs webwww.okayama-international-circuit.jp Okayama International Circuit Co., Ltd.株式会社岡山国際サーキットJenisKabushiki gaishaDidirikanAida (part of Mimasaka), Okayama Prefecture, Japan (13 Agustus ...

Japanese woodblock prints Murder of Ohagi by Saisaburô, Twenty-eight famous murders with verse (1867) Muzan-e (無残絵), also known as Bloody Prints, refers to Japanese woodcut prints of violent nature published in the late Edo and Meiji periods. One of the earliest and most well-known examples is the collection Twenty-Eight Famous Murders with Verse (英名二十八衆句, eimei nijūhasshūku) by the artists Yoshitoshi and Yoshiiku from the 1860s, which depicted several gruesome acts of ...

Period of Japanese history (1532–1555) Part of a series on theHistory of JapanShōsōin ListPaleolithicbefore 14,000 BCJōmon14,000 – 1000 BCYayoi 1000 BC – 300 ADKofun 300 AD – 538 ADAsuka 538 – 710Nara 710 – 794HeianFormer Nine Years' WarLater Three-Year WarGenpei War 794–1185KamakuraJōkyū WarMongol invasionsGenkō WarKenmu Restoration 1185–1333MuromachiNanboku-chō periodSengoku period 1336–1573Azuchi–Momoyama Nanban tradeImjin WarBattl...

Cộng hòa IngushetiyaРеспублика Ингушетия (tiếng Nga)Гӏалгӏай Мохк (Ingush)— Cộng hòa — Quốc kỳ Quốc huy Bài hát: Quốc ca Cộng hòa Ingushetia[1] Toạ độ: 43°12′B 44°58′Đ / 43,2°B 44,967°Đ / 43.200; 44.967Địa vị chính trịQuốc giaLiên bang NgaVùng liên bangBắc Kavkaz[2]Vùng kinh tếBắc Kavkaz[3]Thành lập4 tháng 6 năm 1992[4&#...








































