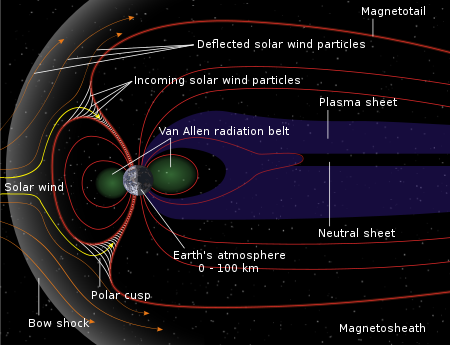
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Second polar moment of area" – news · newspapers · books · scholar · JSTOR (August 2019) (Learn how and when to remove this message) This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: excessive bold and italics. Please help improve this article if you can. (October 2023) (Learn how and when to remove this message) (Learn how and when to remove this message)

The second polar moment of area, also known (incorrectly, colloquially) as "polar moment of inertia" or even "moment of inertia", is a quantity used to describe resistance to torsional deformation (deflection), in objects (or segments of an object) with an invariant cross-section and no significant warping or out-of-plane deformation.^[1] It is a constituent of the second moment of area, linked through the perpendicular axis theorem. Where the planar second moment of area describes an object's resistance to deflection (bending) when subjected to a force applied to a plane parallel to the central axis, the polar second moment of area describes an object's resistance to deflection when subjected to a moment applied in a plane perpendicular to the object's central axis (i.e. parallel to the cross-section). Similar to planar second moment of area calculations (${\displaystyle I_{x}}$,${\displaystyle I_{y}}$, and ${\displaystyle I_{xy}}$), the polar second moment of area is often denoted as ${\displaystyle I_{z}}$. While several engineering textbooks and academic publications also denote it as ${\displaystyle J}$ or ${\displaystyle J_{z}}$, this designation should be given careful attention so that it does not become confused with the torsion constant, ${\displaystyle J_{t}}$, used for non-cylindrical objects.

Simply put, the polar moment of area is a shaft or beam's resistance to being distorted by torsion, as a function of its shape. The rigidity comes from the object's cross-sectional area only, and does not depend on its material composition or shear modulus. The greater the magnitude of the second polar moment of area, the greater the torsional stiffness of the object.

The equation describing the polar moment of area is a multiple integral over the cross-sectional area, ${\displaystyle A}$, of the object.

$${\displaystyle J=\iint _{A}r^{2}\,dA}$$ where ${\displaystyle r}$ is the distance to the element ${\displaystyle dA}$.

Substituting the ${\displaystyle x}$ and ${\displaystyle y}$ components, using the Pythagorean theorem: $${\displaystyle J=\iint _{A}\left(x^{2}+y^{2}\right)dx\,dy}$$ $${\displaystyle J=\iint _{A}x^{2}\,dx\,dy+\iint _{A}y^{2}\,dx\,dy}$$

Given the planar second moments of area equations, where: $${\displaystyle I_{x}=\iint _{A}y^{2}dx\,dy}$$ $${\displaystyle I_{y}=\iint _{A}x^{2}dx\,dy}$$

It is shown that the polar moment of area can be described as the summation of the ${\displaystyle x}$ and ${\displaystyle y}$ planar moments of area, ${\displaystyle I_{x}}$ and ${\displaystyle I_{y}}$ $${\displaystyle \therefore J=I_{z}=I_{x}+I_{y}}$$

This is also shown in the perpendicular axis theorem.^[2] For objects that have rotational symmetry,^[3] such as a cylinder or hollow tube, the equation can be simplified to: $${\displaystyle J=2I_{x}}$$ or $${\displaystyle J=2I_{y}}$$

For a circular section with radius ${\displaystyle R}$: $${\displaystyle I_{z}=\int _{0}^{2\pi }\int _{0}^{R}r^{2}(r\,dr\,d\phi )={\frac {\pi R^{4}}{2}}}$$

The SI unit for polar second moment of area, like the planar second moment of area, is meters to the fourth power (m⁴), and inches to the fourth power (in⁴) in U.S. Customary units and imperial units.

The polar second moment of area can be insufficient for use to analyze beams and shafts with non-circular cross-sections, due their tendency to warp when twisted, causing out-of-plane deformations. In such cases, a torsion constant should be substituted, where an appropriate deformation constant is included to compensate for the warping effect. Within this, there are articles that differentiate between the polar second moment of area, ${\displaystyle I_{z}}$, and the torsional constant, ${\displaystyle J_{t}}$, no longer using ${\displaystyle J}$ to describe the polar second moment of area.^[4]

In objects with significant cross-sectional variation (along the axis of the applied torque), which cannot be analyzed in segments, a more complex approach may have to be used. See 3-D elasticity.

Though the polar second moment of area is most often used to calculate the angular displacement of an object subjected to a moment (torque) applied parallel to the cross-section, the provided value of rigidity does not have any bearing on the torsional resistance provided to an object as a function of its constituent materials. The rigidity provided by an object's material is a characteristic of its shear modulus, ${\displaystyle G}$. Combining these two features with the length of the shaft, ${\displaystyle L}$, one is able to calculate a shaft's angular deflection, ${\displaystyle \theta }$, due to the applied torque, ${\displaystyle T}$: $${\displaystyle \theta ={\frac {TL}{JG}}}$$

As shown, the larger the material's shear modulus and polar second moment of area (i.e. larger cross-sectional area), the greater resistance to torsional deflection.

The polar second moment of area appears in the formulae that describe torsional stress and angular displacement.

Torsional stresses: $${\displaystyle \tau ={\frac {T\,r}{J_{z}}}}$$ where ${\displaystyle \tau }$ is the torsional shear stress, ${\displaystyle T}$ is the applied torque, ${\displaystyle r}$ is the distance from the central axis, and ${\displaystyle J_{z}}$ is the polar second moment of area.

Note: In a circular shaft, the shear stress is maximal at the surface of the shaft.

Calculation of the steam turbine shaft radius for a turboset:

Assumptions:

• Power carried by the shaft is 1000 MW; this is typical for a large nuclear power plant.
• Yield stress of the steel used to make the shaft (τ_yield) is: 250 × 10⁶ N/m².
• Electricity has a frequency of 50 Hz; this is the typical frequency in Europe. In North America the frequency is 60 Hz. This is assuming that there is a 1:1 correlation between rotational velocity of turbine and the frequency of mains power.

The angular frequency can be calculated with the following formula: $${\displaystyle \omega =2\pi f}$$

The torque carried by the shaft is related to the power by the following equation: $${\displaystyle P=T\omega }$$

The angular frequency is therefore 314.16 rad/s and the torque 3.1831 × 10⁶ N·m.

The maximal torque is: $${\displaystyle T_{\max }={\frac {\tau _{\max }J_{z}}{r}}}$$

After substitution of the polar second moment of area the following expression is obtained: $${\displaystyle r={\sqrt[{3}]{\frac {2T_{\max }}{\pi \tau _{\max }}}}}$$

The radius is r=0.200 m = 200 mm, or a diameter of 400 mm. If one adds a factor of safety of 5 and re-calculates the radius with the admissible stress equal to the τ_adm=τ_yield/5 the result is a radius of 0.343 m, or a diameter of 690 mm, the approximate size of a turboset shaft in a nuclear power plant.

Polar second moment of area: $${\displaystyle I_{z}={\frac {\pi \left(D^{4}-d^{4}\right)}{32}}}$$

Moment of inertia: $${\displaystyle I_{c}=I_{z}\rho l={\frac {\pi \rho l\left(D^{4}-d^{4}\right)}{64}}}$$

Polar second moment of area $${\displaystyle I_{z}={\frac {\pi D^{4}}{32}}}$$

Moment of inertia $${\displaystyle I_{c}=I_{z}\rho l={\frac {\pi \rho lD^{4}}{64}}}$$ where:

• ${\displaystyle d}$ is the inner diameter in meters (m)
• ${\displaystyle D}$ is the outer diameter in meters (m)
• ${\displaystyle I_{c}}$ is the moment of inertia in kg·m²
• ${\displaystyle I_{z}}$ is the polar second moment of area in meters to the fourth power (m⁴)
• ${\displaystyle l}$ is the length of cylinder in meters (m)
• ${\displaystyle \rho }$ is the specific mass in kg/m³

• Torsion constant
• Torsion spring
• Torsion bar suspension
• Second moment of area
• Shear modulus
• List of second moments of area

• Torsion of Shafts - engineeringtoolbox.com
• Elastic Properties and Young Modulus for some Materials - engineeringtoolbox.com
• Material Properties Database - matweb.com