Petrov classification
|
Read other articles:

Chronologies Données clés 2009 2010 2011 2012 2013 2014 2015Décennies :1980 1990 2000 2010 2020 2030 2040Siècles :XIXe XXe XXIe XXIIe XXIIIeMillénaires :Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égypte, �...

Bollwillercomune Bollwiller – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Alto Reno ArrondissementGuebwiller CantoneWittenheim TerritorioCoordinate47°52′N 7°15′E / 47.866667°N 7.25°E47.866667; 7.25 (Bollwiller)Coordinate: 47°52′N 7°15′E / 47.866667°N 7.25°E47.866667; 7.25 (Bollwiller) Superficie8,63 km² Abitanti3 609[1] (2009) Densità418,19 ab./km² Altre informazioniCod. postale68540 Fuso...

Former radar station in Lincoln County, Montana Yaak Air Force StationPart of Pine Tree Line[1]Located atHensley Hill[2] in Lincoln County, Montana;[1] 25.1 miles (40.4 km) west of Rexford (eponym: the nearby Town of Yaak) Coordinates48°51′44″N 115°43′18″W / 48.86222°N 115.72167°W / 48.86222; -115.72167 (Yaak AFS P-11)[3]TypeAir Force StationSite informationControlled byAir Defense CommandConditiondemolished...

Cortandonecomune Cortandone – VedutaPanorama LocalizzazioneStato Italia Regione Piemonte Provincia Asti AmministrazioneSindacoClaudio Stroppiana (lista civica Noi per Cortandone) dall'8-6-2009 (3º mandato dal 26-5-2019) TerritorioCoordinate44°57′36″N 8°03′34″E / 44.96°N 8.059444°E44.96; 8.059444 (Cortandone)Coordinate: 44°57′36″N 8°03′34″E / 44.96°N 8.059444°E44.96; 8.059444 (Cortandone) Altitudine21...

Pesta Olahraga Difabel Asia Tenggara XIITuan rumahPhnom PenhMotoSports Live in PeaceJumlah negara11Jumlah atlet1453Jumlah disiplin439 acara dalam 12 cabang olahragaUpacara pembukaan3 JuniUpacara penutupan9 JuniDibuka olehHun SenPerdana Menteri KambojaPenyalaan oborSinet AnTempat utamaStadion Nasional Morodok TechoSitus webhttps://www.cambodia2023.com← Surakarta 2022 Nakhon Ratchasima 2026 → Pesta Olahraga Difabel Asia Tenggara 2023, yang secara resmi dikenal sebagai bahasa Inggris...

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

Grand Prix Belgia 2011 Lomba ke-12 dari 19 dalam Formula Satu musim 2011← Lomba sebelumnyaLomba berikutnya → Tata letak sirkuit Spa-Francorchamps.Detail perlombaan[1]Tanggal 28 Agustus 2011Nama resmi 2011 Formula 1 Shell Belgian Grand Prix[2]Lokasi Sirkuit Spa-Francorchamps, Francorchamps, Wallonia, BelgiaSirkuit Fasilitas balapan permanenPanjang sirkuit 7.004 km (4.352 mi)Jarak tempuh 44 putaran, 308.052 km (191.415 mi)Cuaca Berawan, keringPosisi poleP...
2020年夏季奥林匹克运动会马来西亚代表團马来西亚国旗IOC編碼MASNOC马来西亚奥林匹克理事会網站olympic.org.my(英文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員30參賽項目10个大项旗手开幕式:李梓嘉和吳柳螢(羽毛球)[1][2]閉幕式:潘德莉拉(跳水)[3]獎牌榜排名第74 金牌 銀牌 銅�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2017) منظمة الاتحاد العام للمرأة السورية البلد سوريا تعديل مصدري - تعديل منظمة الاتحاد العام للمرأة السورية، هي منظمه غير ممولة من الحكومة السورية ولكنها ...

اقتصاد أيرلندا الشماليةعامالدولة المملكة المتحدة عملة جنيه إسترليني الإحصائياتنصيب الفرد من الناتج الإجمالي 23700 دولار أمريكي[1](2015) تعديل - تعديل مصدري - تعديل ويكي بيانات بلفاست يُعدّ اقتصاد أيرلندا الشمالية الأصغر بين الدول الأربعة للمملكة المتحدة. في السابق كانت أي...

Cristóbal López RomeroS.D.B.Uskup Agung RabatGerejaGereja KatolikKeuskupan agungRabatTakhtaRabatPenunjukan29 Desember 2017Awal masa jabatan10 Maret 2018PendahuluVincent Louis Marie LandelJabatan lainAdministrator Apostolik Tanger (2019-)Kardinal-Imam San Leone I (2019-)ImamatTahbisan imam19 Mei 1979oleh Narciso Jubany ArnauTahbisan uskup10 Maret 2018oleh Juan José OmellaPelantikan kardinal5 Oktober 2019oleh Paus FransiskusPeringkatKardinal-ImamInformasi pribadiNama lahirCristóba...

Double-walled sac containing the heart and roots of the great vessels For the Traditional Chinese medicine description, see Pericardium (Chinese medicine). Pericard redirects here. For the footballer, see Vincent Pericard. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Pericardium – news · newspapers · books · sc...

City in West Virginia, United StatesMadisonCityMain Street in Madison in 2007Nickname: The Gateway to the Coal FieldsLocation of Madison in Boone County, West Virginia.Coordinates: 38°3′43″N 81°49′6″W / 38.06194°N 81.81833°W / 38.06194; -81.81833CountryUnited StatesStateWest VirginiaCountyBooneArea[1] • Total7.06 sq mi (18.29 km2) • Land7.01 sq mi (18.14 km2) • Water0.06 sq...
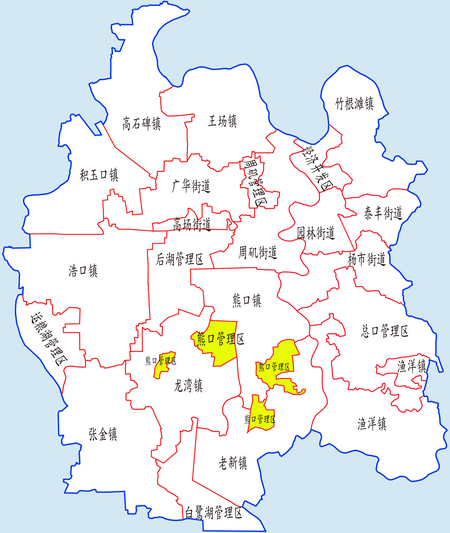
County-level & Sub-prefectural city in Hubei, People's Republic of ChinaQianjiang 潜江市Tsienkiang, Ch’ien-chiangCounty-level & Sub-prefectural cityLocation of Qianjiang City jurisdiction in HubeiQianjiangLocation of the city centre in HubeiCoordinates (Qianjiang government): 30°24′07″N 112°54′01″E / 30.4019°N 112.9003°E / 30.4019; 112.9003CountryPeople's Republic of ChinaProvinceHubeiArea • County-level & Sub-prefectural ci...

مادس هيرمانسن معلومات شخصية الميلاد 11 يوليو 2000 (العمر 24 سنة)أودنسه الطول 1.85 م (6 قدم 1 بوصة) مركز اللعب حارس مرمى الجنسية الدنمارك معلومات النادي النادي الحالي بروندبي الرقم 1 مسيرة الشباب سنوات فريق Næsby Boldklub [الإنجليزية] 2015–2019 بروندبي المسيرة الاحت�...

United States Marine Corps officer and writer (1875–1936) George Cyrus ThorpeThorpe aboard the USS Tennessee, c. 1909Born(1875-01-07)January 7, 1875Northfield, Minnesota, U.S.DiedJuly 28, 1936(1936-07-28) (aged 61)Bethesda, Maryland, U.S.Place of burialArlington National CemeteryAllegianceUnited StatesService/branchUnited States Marine CorpsYears of service1898–1923RankColonelUnit1917–1918, Chief of Staff, 2nd Marine BrigadeCommands held 1903, Marine guard for U.S. diplo...

Untuk penari balet Kanada, lihat Lois Smith (penari). Lois SmithSmith pada 1955LahirLois Arlene Humbert03 November 1930 (umur 93)Topeka, Kansas, ASAlmamaterUniversitas Washington (keluar)PekerjaanPemeranTahun aktif1952–sekarangSuami/istriWesley Smith (m. 1948; bercerai 1970)Anak1 Penghargaan(2006) Lucille Lortel Award for Outstanding Lead Actress (en) (2006) Drama Desk Award for Outstanding Actress in a Play (en) (1970) Aktris Pe...

第三十二届夏季奥林匹克运动会女子10公里马拉松游泳比賽奖牌得主比賽場館御台場海濱公園日期2021年8月4日参赛选手25位選手,來自23個國家和地區冠军成绩1:59:30.8奖牌获得者01 ! 安娜·玛赛拉·库尼亚 巴西02 ! 莎龙·范劳文达尔 荷兰03 ! 卡里娜·李 澳大利亚← 20162024 → 2020年夏季奥林匹克运动会游泳比赛自由泳50米男子女子100米男子女子200...

Die hier wiedergegebene Systematik der Bakterien gilt in der Wikipedia als Referenz; dies betrifft insbesondere die Einträge in Taxoboxen. Staphylococcus aureus (nachträglich kolorierte REM-Aufnahme) Die taxonomische Aufteilung der Bakterien und Archaeen ist umstritten. Anfangs nur durch Aussehen und Physiologie klassifiziert, wird heute aufgrund neuer Möglichkeiten allgemein die Einteilung mittels phylogenetischer Analyse akzeptiert, wie es Carl Woese (1977, 1990) vorgeschlagen hat.[...

Questa voce o sezione sull'argomento Competizioni calcistiche non è ancora formattata secondo gli standard. Commento: Si invita a seguire il modello di voce Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. First Division 1994-1995 Competizione First Division Sport Calcio Edizione 92ª Organizzatore Federazione calcistica dell'Inghilterra Date dal 1994 Luogo Inghilterra Partecipanti 24 Formula 1 girone all'italia...






![{\displaystyle U_{ab}=-2l_{[a}{\bar {m}}_{b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f00ebe4daf6642fb1f7a848e9074b6264c087dc)
![{\displaystyle V_{ab}=2n_{[a}m_{b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc653ce04c24d51ec78cf836aea4c2644687fa3)
![{\displaystyle W_{ab}=2m_{[a}{\bar {m}}_{b]}-2n_{[a}l_{b]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f478eeee44ef0a29785ef215f2cec27c0dffafc)

































