PSL(2,7)
|
Read other articles:

Cet article est une ébauche concernant l’administration territoriale et l’Angleterre. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Angleterre du Sud-EstNom officiel (en) South East EnglandNom local (en) South East EnglandGéographiePays Royaume-UniNation constitutive AngleterreSuperficie 19 096 km2Coordonnées 51° 18′ N, 0° 48′ ODémographiePopulation 9,4 M ...

حلقات زحلمعلومات عامةصنف فرعي من حلقة كوكبية المكتشف أو المخترع كريستيان هوغنس[1] زمن الاكتشاف أو الاختراع 1656[1] الجرم السماوي الأم زحل لديه جزء أو أجزاء حاجز كاسينيPhoebe ring (en) gap in the rings of Saturn (en) تعديل - تعديل مصدري - تعديل ويكي بيانات طغت على المجموعة الكاملة من حلقات ر...

Pemandangan Semarang dari udara Kota Semarang adalah ibu kota Jawa Tengah. Gedung tertinggi di Semarang yang pertama kali adalah kantor pemerintah Provinsi Jawa Tengah 12 lantai yang berdiri tahun 1987, diikuti Hotel Santika 12 lantai yang berdiri tahun 1990 dan Hotel Ciputra 12 lantai yang berdiri tahun 1993.[1] Pembangunan gedung tinggi Semarang terkendala di bawah 12 lantai sesuai aturan Kawasan Keselamatan Operasi Penerbangan karena Bandar Udara Internasional Achmad Yani di dalam ...

This is the list of cathedrals in the Dominican Republic sorted by denomination. Anglican Catedral de la Epifania/Union Church, Santo Domingo (The Episcopal Church) Catedral Primada de América, Ciudad Colonial, Santo Domingo Roman Catholic Cathedrals of the Roman Catholic Church in the Dominican Republic:[1] Basilica Cathedral of Santa María la Menor (Catedral Primada de América) (Spanish: Basílica Menor de Santa María de la Encarnación), Ciudad Colonial, Santo Domingo Basílic...

الدوري الفنلندي الممتاز 2019 تفاصيل الموسم الدوري الفنلندي الممتاز النسخة 110 البلد فنلندا التاريخ بداية:3 أبريل 2019 نهاية:3 نوفمبر 2019[1] البطل كووبيون بالوسيورا[2] مباريات ملعوبة 132 عدد المشاركين 12 الدوري الفنلندي الممتاز 2018 الدوري الفنلن...
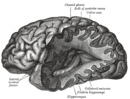
Philosophy of neuroscience This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (January 2018) (Learn how and when to remove this message) This article is written like a personal reflection, personal ess...

House museum in Ontario, CanadaBillings Estate MuseumEstablished1975; 49 years ago (1975)LocationOttawa, Ontario, CanadaTypehouse museumWebsite[1] National Historic Site of CanadaOfficial nameBillings House National Historic Site of CanadaDesignated1968 The Billings Estate National Historic Site is a heritage museum in Ottawa, Ontario, Canada. It is located at 2100 Cabot St. in the former home of one of the region's earliest settlers. The oldest wood-framed house in Ottawa ...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

Kerucut hop di ladang hop di Hallertau, Jerman. Hop adalah sekumpulan bunga betina (disebut benih kerucut atau strobilus), dari spesies hop, Humulus lupulus.[1] Hop umumnya digunakan sebagai perasa dan penstabil rasa bir, di mana mereka menambah rasa pahit dan asam. Hop juga digunakan dalam pembuatan minuman lain dan juga dalam pembuatan jamu. Hop telah di budidaya kan secara terus menerus sejak abad ke-8 atau ke-9 sesudah Masehi di kebun Bohemia di distrik Hallertau di Bavaria dan da...

Australian Army officer and Governor of Tasmania (1928–2023) For other people named Phillip Bennett, see Phillip Bennett (disambiguation). GeneralSir Phillip BennettAC, KBE, DSOBennett in 199223rd Governor of TasmaniaIn office19 October 1987 – 2 October 1995MonarchElizabeth IIPremierRobin Gray Michael Field Ray GroomPreceded bySir James PlimsollSucceeded bySir Guy Green Personal detailsBorn(1928-12-27)27 December 1928Perth, Western Australia, AustraliaDied1 Au...

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Boğaziçi University di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan pe...

American judge (born 1950) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: George H. Wu – news · newspapers · books · scholar · JSTOR (September 2021) (Learn how and when to remove this message...

American regional sports network For the original SportSouth (1990-1996), see Bally Sports South. Television channel Bally Sports SoutheastTypeRegional sports networkCountryUnited StatesBroadcast areaGeorgiaTennesseeAlabamaMississippiSouth Carolinaparts of North Carolina including Asheville, Charlotte, and Winston-SalemNationwide (via satellite)NetworkBally SportsHeadquartersAtlanta, GeorgiaProgrammingLanguage(s)EnglishPicture format720p (HDTV)480i (SDTV)OwnershipOwnerDiamond Sports GroupPare...

51°30′47.7″N 0°5′21.7″W / 51.513250°N 0.089361°W / 51.513250; -0.089361 Mansion HouseInformasi umumGaya arsitekturPalladianKotaLondon, EC4NegaraBritania RayaPenyewa sekarangLord Mayor LondonMulai dibangun1739Desain dan konstruksiArsitekGeorge Dance the ElderSitus webMansion House Mansion House adalah kediaman resmi Lord Mayor London, yaitu wali kota City of London (tidak sama dengan Wali Kota London yang mencakup seluruh wilayah London Raya). Gedung ini dib...

New Testament manuscript Papyrus 𝔓86New Testament manuscriptNamePap. Col. 5516TextGospel of Matthew 5 †Date4th centuryScriptGreekFoundEgyptNow atUniversity of CologneCiteCharalambakis-Hagedorn-Kaimakis-Thüngen, Vier literarische Papyri der Kölner Sammlung, ZPE 14 (Barcelona: 1974), pp. 37-40.TypeAlexandrian text-typeCategoryII Papyrus 86 (in the Gregory-Aland numbering), designated by siglum 𝔓86, is an early copy of the New Testament in Greek. It is a papyrus manuscript of the ...

Cet article est une ébauche concernant les mollusques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations du projet zoologie. Pectinida Aequipecten opercularisClassification WoRMS Règne Animalia Embranchement Mollusca Classe Bivalvia Sous-classe Pteriomorphia OrdrePectinidaGray, 1854 Les Pectinida sont un ordre de mollusques bivalves, dont de nombreuses espèces sont dénommées « pétoncles ». Les familles de l'ordre des Pectin...

Statue by Angela Conner Statue of Charles de GaulleArtistAngela ConnerYear1993LocationCarlton Gardens, London A bronze statue of Charles de Gaulle stands in Carlton Gardens in the City of Westminster, London. Charles de Gaulle, the leader of Free France, set up his government in exile at No. 4 Carlton Gardens.[1] The statue was campaigned for by Mary Soames, the daughter of De Gaulle's contemporary Winston Churchill.[2] It was unveiled by Queen Elizabeth The Queen Mother on 23...

Chief commanding authority of the Russian Ground ForcesThis article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Commander-in-Chief of the Russian Ground Forces – news · newspapers · books · scholar · JSTOR (September 2018) Commander-in-Chief of the Russian Ground ForcesГлавнокомандующие С�...

Football stadium in Honduras Francisco Martínez DurónFull nameEstadio Francisco Martínez DurónLocationTocoa, Colón, HondurasCoordinates15°39′20″N 85°59′18″W / 15.65556°N 85.98833°W / 15.65556; -85.98833Capacity3,000SurfaceGrassConstructionOpened1986Renovated2012Expanded2012TenantsReal SociedadBoca Juniors de Tocoa Estadio Francisco Martínez Durón is a football stadium in Tocoa, Honduras. It is currently used mostly for football matches and is the hom...

Gange Le Gange à Varanasi. Carte des bassins versants combinés du Gange (orange), du Brahmapoutre (violet), et du Meghna (vert). Caractéristiques Longueur 2 510 km Bassin 907 000 km2 Bassin collecteur Bassin du Gange Débit moyen 16 648 m3/s (Barrage de Farakka) Régime Pluvial de mousson Cours Source Confluent du Bhagirathi et de l'Alaknanda · Localisation Devprayag (Uttarakhand) Inde · Altitude 459 m · Coordonnées 30° 08′ 42,02″ ...





