Negligible set

In mathematics, a negligible set is a set that is small enough that it can be ignored for some purpose. As common examples, finite sets can be ignored when studying the limit of a sequence, and null sets can be ignored when studying the integral of a measurable function.

Negligible sets define several useful concepts that can be applied in various situations, such as truth almost everywhere. In order for these to work, it is generally only necessary that the negligible sets form an ideal; that is, that the empty set be negligible, the union of two negligible sets be negligible, and any subset of a negligible set be negligible. For some purposes, we also need this ideal to be a sigma-ideal, so that countable unions of negligible sets are also negligible. If I and J are both ideals of subsets of the same set X, then one may speak of I-negligible and J-negligible subsets.

The opposite of a negligible set is a generic property, which has various forms.

Examples

Let X be the set N of natural numbers, and let a subset of N be negligible if it is finite. Then the negligible sets form an ideal. This idea can be applied to any infinite set; but if applied to a finite set, every subset will be negligible, which is not a very useful notion.

Or let X be an uncountable set, and let a subset of X be negligible if it is countable. Then the negligible sets form a sigma-ideal.

Let X be a measurable space equipped with a measure m, and let a subset of X be negligible if it is m-null. Then the negligible sets form a sigma-ideal. Every sigma-ideal on X can be recovered in this way by placing a suitable measure on X, although the measure may be rather pathological.

Let X be the set R of real numbers, and let a subset A of R be negligible if for each ε > 0,[1] there exists a finite or countable collection I1, I2, … of (possibly overlapping) intervals satisfying:

and

This is a special case of the preceding example, using Lebesgue measure, but described in elementary terms.

Let X be a topological space, and let a subset be negligible if it is of first category, that is, if it is a countable union of nowhere-dense sets (where a set is nowhere-dense if it is not dense in any open set). Then the negligible sets form a sigma-ideal.

Let X be a directed set, and let a subset of X be negligible if it has an upper bound. Then the negligible sets form an ideal. The first example is a special case of this using the usual ordering of N.

In a coarse structure, the controlled sets are negligible.

Derived concepts

Let X be a set, and let I be an ideal of negligible subsets of X. If p is a proposition about the elements of X, then p is true almost everywhere if the set of points where p is true is the complement of a negligible set. That is, p may not always be true, but it's false so rarely that this can be ignored for the purposes at hand.

If f and g are functions from X to the same space Y, then f and g are equivalent if they are equal almost everywhere. To make the introductory paragraph precise, then, let X be N, and let the negligible sets be the finite sets. Then f and g are sequences. If Y is a topological space, then f and g have the same limit, or both have none. (When you generalise this to a directed sets, you get the same result, but for nets.) Or, let X be a measure space, and let negligible sets be the null sets. If Y is the real line R, then either f and g have the same integral, or neither integral is defined.

See also

References

  1. ^ Billingsley, P. (1995). Probability and Measure (Third ed.). New York: John Wiley & Sons. p. 8. ISBN 0-471-00710-2.

Read other articles:

Artigues-près-Bordeaux

Artigues-près-BordeauxArtigues-près-Bordeaux Koordinat: 44°51′46″N 0°29′06″W / 44.8627777778°N 0.485°W / 44.8627777778; -0.485NegaraPrancisArondisemenBordeauxKantonCenonAntarkomuneBordeauxPemerintahan • Wali kota (2008-2014) Françoise Cartron • Populasi15.984Kode INSEE/pos33013 / 2 Population sans doubles comptes: penghitungan tunggal penduduk di komune lain (e.g. mahasiswa dan personil militer). Artigues-près-Bordeaux merup...

 

Cantal (keju)

CantalNegara asalPrancisKawasan, kotaCantalSumber susuSapiDipasteurisasiYaTeksturKerasKadar lemak45%Waktu pematanganSetidaknya satu bulanSertifikasiAOC: 1956[1] Cantal adalah keju dari daerah dengan nama sama di Prancis dan diproduksi dengan menggunakan susu sapi yang dipasteurisasi.[1] Keju ini berasal dari Pays Vert di Auvergne dan diproduksi di seluruh daerah di departemen Cantal dan di 41 desa di departemen Aveyron, Corréze, Haute-Loire, dan Puy-de-Dôme.[1] Keju ...

 

Kriket pada Pekan Olahraga Nasional 2016

Kriket pada Pekan Olahraga Nasional 2016LokasiStadion Siliwangi, Kota BandungTanggal18–26 September 2016← Kompetisi Perdana2021 → Kriket dipertandingkan di PON XIX/2016, dari tanggal 18 sampai 26 september 2016, di Stadion Siliwangi, Kota Bandung, Jawa Barat.[1] Penyelenggaraan pada PON XIX/2016 merupakan debut bagi cabang olahraga Kriket di Pekan Olahraga Nasional.[2][3] Kualifikasi Jenis Kualifikasi Tanggal Tuan rumah Kuota Tim Putra Putri Pro...

Hilde Vautmans

Belgian politician Hilde VautmansMEPMember of the European ParliamentIncumbentAssumed office 1 January 2015Preceded byAnnemie Neyts-UyttebroeckConstituencyDutch-speaking electoral college of Belgium Personal detailsBorn2 May 1972 (1972-05-02) (age 51)Sint-Truiden, BelgiumPolitical partyOpen Vlaamse Liberalen en DemocratenOccupationPolitician Hilde Vautmans (born 2 May 1972) is a Belgian politician of the Open Vlaamse Liberalen en Democraten who has been serving as a Member of th...

 

Willybrodus Lay

Willybrodus Lay Bupati Belu ke-9Masa jabatan17 Februari 2016 – 17 Februari 2021PresidenJoko WidodoGubernurFrans Lebu RayaRobert Simbolon (Pj.)Viktor LaiskodatWakilJ. T. Ose Luan PendahuluWilhelmus Foni (Pj.)Penggantidr. Taolin Agustinus, SpPD-KGEH, FINASIMKetua Umum DPC Partai Demokrat Kabupaten BeluMasa jabatan2006–2021PresidenSusilo Bambang YudoyonoJoko Widodo Informasi pribadiLahir18 Juni 1961 (umur 62)[1] Atambua, Nusa Tenggara TimurKebangsaan IndonesiaP...

 

Massacro d'Odessa

Disambiguazione – Se stai cercando l'incendio del 2014, vedi Incendio della Casa dei sindacati di Odessa. Massacro d'OdessaColonna di civili ebrei deportati in Transnistria scortati da soldati rumeni. Tipostrage Data22-24 ottobre 1941 LuogoOdessa Stato Unione Sovietica Coordinate46°27′57.6″N 30°43′58.8″E / 46.466°N 30.733°E46.466; 30.733Coordinate: 46°27′57.6″N 30°43′58.8″E / 46.466°N 30.733°E46.466; 30.733 ObiettivoEbreiRom Resp...

Nok Air

Nok Airนกแอร์ IATA ICAO Kode panggil DD NOK NOK AIR Didirikan10 Februari 2004Mulai beroperasi23 Juli 2004PenghubungBangkok-Don MueangChiang MaiPhuketAliansiValue AllianceArmada33Tujuan36SloganSmiling Across AsiaPerusahaan indukNok Airlines Public Company LimitedKantor pusatBangkok, ThailandTokoh utamaDr Wutthiphum Jurangkool (CEO)Situs webhttp://www.nokair.com Nok Air (Bahasa Thai: นกแอร์) adalah maskapai penerbangan bertarif rendah yang berpusat di Bangkok, Thailand. ...

 

Messerschmitt Bf 109 operational history

The Messerschmitt Bf 109 was a German World War II fighter aircraft designed by Willy Messerschmitt and Robert Lusser during the early to mid-1930s. It was one of the first true modern fighters of the era, including such features as all-metal monocoque construction, a closed canopy, a retractable landing gear, and was powered by a liquid-cooled, inverted-V12 aero engine. The Bf 109 saw active service in many air forces and was active in several conflicts outside of World War II. Combat servic...

 

Minimum wage in Canada

Minimum wage laws in Canada Under the Constitution of Canada, the responsibility for enacting and enforcing labour laws, including the minimum wage, rests primarily with the ten Provinces of Canada. The three Territories of Canada have a similar power, delegated to them by federal legislation. Some provinces allow lower wages to be paid to liquor servers and other gratuity earners or to inexperienced employees. The Government of Canada has the constitutional authority to set minimum wages onl...

1991 en musique classique

Chronologies Données clés 1988 1989 1990  1991  1992 1993 1994Décennies :1960 1970 1980  1990  2000 2010 2020Siècles :XVIIIe XIXe  XXe  XXIe XXIIeMillénaires :-Ier Ier  IIe  IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égyp...

 

大字 (数字)

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

 

Державний комітет телебачення і радіомовлення України

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна  УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

Liberty Street (TV series)

Canadian TV series or program Liberty StreetWritten byWilliam FlahertyJackie MayDirected byGail HarveyNicholas KendallStarringPat MastroianniKimberly HuieJoel BissonnetteHenriette IvanansBilly MerastyMarcia LaskowskiL. Dean IfillOpening themeRitual by Cowboy JunkiesCountry of originCanadaOriginal languageEnglishNo. of seasons2No. of episodes26ProductionProduction locationsToronto, Ontario, CanadaRunning time30 minutesProduction companyEpitome PicturesOriginal releaseNetworkCBC TelevisionRele...

 

Australian Senate committees

For consideration of bills by the Senate 'in committee', see Committee of the Whole. This article is part of a series on thePolitics ofAustralia Constitution The Crown Monarch Charles III Governor-General David Hurley Executive Prime Minister Anthony Albanese (ALP) Deputy Prime Minister Richard Marles (ALP) Federal Executive Council Ministry Albanese ministry Cabinet Legislature Australian Parliament Senate President Sue Lines (ALP) Leader Penny Wong (ALP) House of Representatives Speaker Mi...

 

Piaranthus

Genus of flowering plants Piaranthus Piaranthus geminatus in cultivation Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Asterids Order: Gentianales Family: Apocynaceae Subfamily: Asclepiadoideae Tribe: Ceropegieae Genus: PiaranthusR.Br. (1810) Synonyms[1] Huerniopsis N.E.Br. (1878) Obesia Haw. (1812) Piaranthus is a succulent plant genus in the subfamily Asclepiadoideae, in the family Apocynaceae. It was first described in 181...

Return of Jesus to Galilee

Episode in the life of Jesus For the return after the flight into Egypt, see Return of the family of Jesus to Nazareth. Return of Jesus to Galilee depicted in the Bowyer Bible, 19th century. The Return of Jesus to Galilee is an episode in the life of Jesus which appears in three of the Canonical Gospels: Matthew 4:12, Mark 1:14 and John 4:1–3, 4:43–45. It relates the return of Jesus to Galilee upon the imprisonment of John the Baptist.[1] Gospel of John Map of Judea, Samaria and G...

 

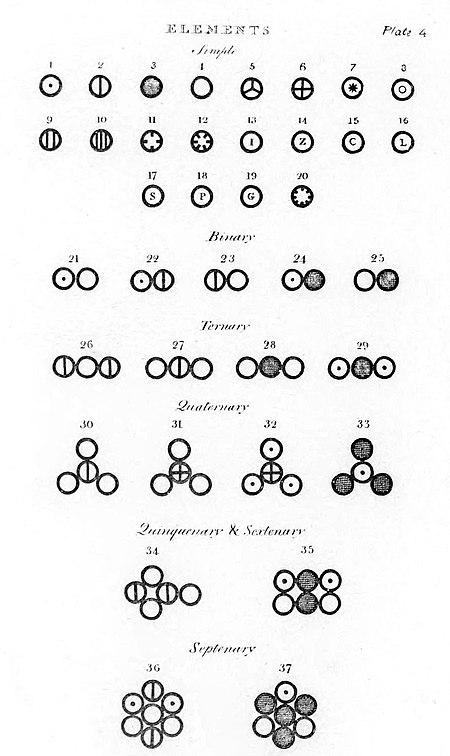
Simbolo chimico

Simboli utilizzati da John Dalton per rappresentare gli elementi chimici (A New System of Chemical Philosophy, 1808). Un simbolo chimico è un'abbreviazione o una rappresentazione accorciata del nome di un elemento chimico. Tutti gli elementi hanno un simbolo chimico di una (ad esempio C per il carbonio) o due (Li per il litio) lettere; alcuni degli elementi creati artificialmente possiedono un simbolo provvisorio di tre lettere (Uup per l'ununpentio). Indice 1 Caratteristiche 2 Bibliografia ...

 

Logika pass-transistor

Rangkaian CMOS dengan 6 buah rangkaian transistor untuk sel memori SRAM. Bagian M5 dan M6 adalah pass transistor dua arah. Dalam bidang elektronika, Logika pass-transistor atau pass-transistor logic (PTL) adalah salah satu jenis logika rangkaian elektronik yang digunakan dalam suatu desain sirkuit terpadu. Penggunaan dari rangkaian ini dapat mengurangi jumlah transistor yang dipakai untuk merealisasikan berbagai gerbang logika, serta dapat menghilangkan bagian transistor yang tidak diperlukan...

2008 Maltese general election

2008 Maltese general election ← 2003 8 March 2008 2013 →   First party Second party   Leader Lawrence Gonzi Alfred Sant Party Nationalist Labour Last election 51.79%, 35 seats 47.51%, 30 seats Seats won 35 34 Seat change 4 Popular vote 143,468 141,888 Percentage 49.34% 48.79% Swing 2.45pp 1.28pp Prime Minister before election Lawrence Gonzi Nationalist Elected Prime Minister Lawrence Gonzi Nationalist Politics of Malta Republic Constitution...

 

Itezhi-Tezhi (constituency)

Zambian National Assembly constituency Politics of Zambia Constitution Human rights Government President Hakainde Hichilema Vice-President Mutale Nalumango Cabinet Legislature National Assembly Speaker: Nelly Mutti Constituencies Judiciary Constitutional Court President: Mulela Margaret Munalula Supreme Court Chief Justice: Mumba Malila Elections General 1964 1968 1973 1978 1983 1988 1991 1996 2001 2006 2011 2016 2021 Presidential 2008 2015 Referendums 1969 2016 Political parties By-elections...