Read other articles:

Cet article est une ébauche concernant le chemin de fer et le Japon. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. SkylinerPrésentationType Service de métro/train vers un aéroport (en), limited express (en)Fondation 1972Longueur 64 100 mPropriétaire KeiseiGestionnaire KeiseiSite web (mul) www.keisei.co.jp/keisei/tetudou/skylinerLocalisationLocalisation préfecture de Chiba Japonmodifier - m...

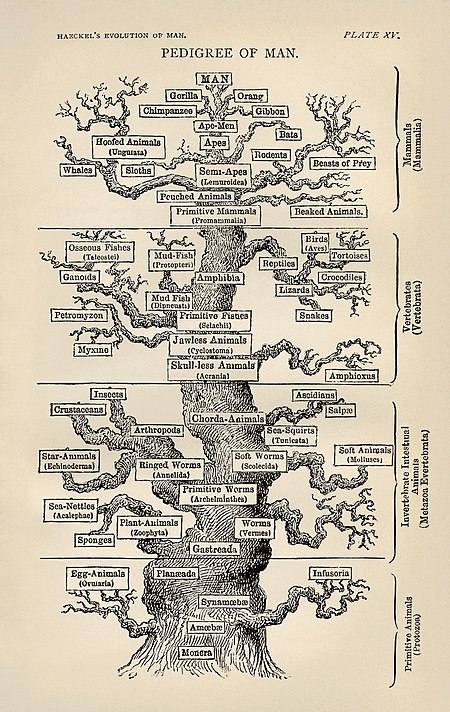
Branch of biology that studies living organisms Not to be confused with Neonatology. Neontology is a part of biology that, in contrast to paleontology, deals with living (or, more generally, recent) organisms. It is the study of extant taxa (singular: extant taxon): taxa (such as species, genera and families) with members still alive, as opposed to (all) being extinct. For example: The moose (Alces alces) is an extant species, and the Irish elk (Megaloceros giganteus) is an extinct species. I...

Recurring character on Saturday Night Live Hanukkah Harry is a fictional character on Saturday Night Live played by Jon Lovitz. Hanukkah Harry is portrayed on the show as a variation upon the modern-day image of Santa Claus, with a beard characteristic of a male adherent of Haredi Judaism, and with his hat in blue with white edges (the colors of an Ashkenazi Jewish tallit,[citation needed] or prayer shawl, shared by the flag of Israel). Saturday Night Live Jon Lovitz (2008) Hanukkah H...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Married... with ChildrenPembuatMichael G. MoyeRon LeavittPemeranEd O'NeillKatey SagalChristina ApplegateDavid FaustinoAmanda BearseDavid GarrisonT...

2019 song by Eliot Vassamillet Wake UpSingle by Eliot VassamilletReleased2019Length2:59LabelSony MusicSongwriter(s)Pierre DumoulinEliot VassamilletProducer(s)Pierre DumoulinEurovision Song Contest 2019 entryCountryBelgiumArtist(s)Eliot VassamilletLanguageEnglishComposer(s)Pierre DumoulinEliot VassamilletLyricist(s)Pierre DumoulinEliot VassamilletFinals performanceSemi-final result13thSemi-final points70Entry chronology◄ A Matter of Time (2018)Release Me (2020) ► Wake Up is a song by Belgi...

 本表是動態列表，或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源，曾潛伏於中華民國國軍、被中國共產黨聲稱或承認，或者遭中華民國政府調查審判，為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準，正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Кача — етап історії вітчизняної авіації УкраїнаНомінал 5 гривеньМаса 16,54 гДіаметр 35 ммГурт рифленийМетал нейзильберРоки карбування 2012Аверс Реверс «Ка́ча — ета́п істо́рії вітчизня́ної авіа́ції» — ювілейна монета номіналом 5 гривень, випущена Націонал�...

Клементина Австрийскаянем. Maria Klementine Franziska Josepha von Österreich эрцгерцогиня Австрийскаяпринцесса Салерно Рождение 1 марта 1798(1798-03-01)Вена Смерть 3 сентября 1881(1881-09-03) (83 года)Шантийи Место погребения Санта-КьяраКоролевская капелла в Дрё Род Габсбурги Сицилийские Бурбоны (по муж...

Squall Leonhart Dissidia oleh Tetsuya Nomura[1] Squall Leonhart (スコール・レオンハートcode: ja is deprecated , Sukōru Reonhāto) adalah tokoh utama RPG Squaresoft (sekarang Square Enix) Final Fantasy VIII. Ia didesain oleh Tetsuya Nomura dengan pengaruh besar yang datang dari sutradara game Yoshinori Kitase. Sebagai karakter utama dalam Final Fantasy VIII, sebagian besar permainan dilihat dari perspektif Squall. Limit Break Squall adalah Renzokuken, yang mana merupakan sa...

This article is about the 1964 film. For the 1976 film, see Shoot (film). 1964 filmThe ShootDirected byRobert SiodmakWritten byKarl May (novel)Georg MarischkaRobert SiodmakProduced byArtur BraunerGötz Dieter WulfHeinz WillegStarringLex BarkerMarie VersiniRalf WolterCinematographyAleksandar SekulovicEdited byUrsula KahlbaumMusic byMartin BöttcherProductioncompaniesCCC FilmSerena FilmCriterion FilmAvala FilmHoche ProductionsRegina FilmDistributed byGloria FilmRelease date 20 August ...

Nicanor Plaza Nicanor PlazaInformación personalNacimiento 1844Santiago de Chile, ChileFallecimiento 2 de mayo de 1918Florencia, ItaliaNacionalidad ChilenaInformación profesionalOcupación Escultor [editar datos en Wikidata] Nicanor Plaza Águila (Santiago de Chile, 1844 - Florencia, Italia, 7 de diciembre de 1918) fue un escultor y profesor de arte chileno, autor de obras inspiradas en la historia. Biografía Estatua de Andrés Bello en la Casa Central de la Universidad de Chile, ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Balisong. Balisong, pisau kipas, pisau kupu-kupu atau pisau Batangas, adalah jenis pisau lipat khas yang berasal dari Filipina. Berbeda dengan pisau lipat biasa, pisau ini memiliki dua gagang yang berputar berlawanan di sekitar tangkai gagang, sehingga...

2001 film by David Weaver and Bridget Newson This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Century Hotel – news · newspapers · books · scholar · JSTOR (April 2019) (Learn how and when to remove this message) Century HotelDVD coverDirected byDavid WeaverWritten byDavid WeaverBridget NewsonProduced byVictori...

Right triangle with a feature making calculations on the triangle easier 90-45-45 triangle and 30-60-90 triangle redirect here. For the drawing tool, see Set square. Position of some special triangles in an Euler diagram of types of triangles, using the definition that isosceles triangles have at least two equal sides, i.e. equilateral triangles are isosceles. A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which si...

Malaysian footballer (1948–2018) In this Chinese name, the family name is Qiú (仇). Chow Chee Keong Chee Keong playing for South ChinaPersonal informationDate of birth (1948-11-26)26 November 1948Place of birth Kuala Lumpur, MalaysiaDate of death 21 February 2018(2018-02-21) (aged 69)Height 1.80 m (5 ft 11 in)Position(s) GoalkeeperSenior career*Years Team Apps (Gls)1967–1968 Bedford Town (0)1970 HK Rangers (0)1970–1971 Jardine (0)1971–1974 South China (0)1974–1...

Political party in United States New Jersey Conservative Party ChairmanDr. Steven ManessFounded1992[1]IdeologyAmerican nationalismStates' rightsConservatismPolitical positionCenter-right to right-wingWebsitehttp://www.conservativepartynj.org/Politics of United StatesPolitical partiesElections The New Jersey Conservative Party, formerly abbreviated as the NJCP, now as CP-NJ, is a conservative political party in New Jersey, United States. Ideology The NJCP advocates for low tax...

15th-century castle, now a hotel, Dublin, Ireland Luttrellstown CastleAn illustration of the castle by Rose Barton in 1898.Alternative namesWoodlandsGeneral informationStatusHotelArchitectural styleGothic, GeorgianTown or cityClonsilla, DublinCountryIrelandGroundbreaking1787-94 (for Henry Luttrell)Estimated completion1810 (extended and remodelled)Design and constructionOther designersBartholomew Byrne - stucco work (1794)Quantity surveyorBryan Bolger (1794)Main contractorG&T Crampton (198...

No debe confundirse con el Delta de Dirac ni con el Símbolo de Kronecker. En matemáticas, la delta de Kronecker (llamada así en referencia al matemático alemán Leopold Kronecker) es una función de dos variables, generalmente solo números enteros no negativos. La función vale 1 si las dos variables son iguales y 0 en caso contrario: δ i j = { 0 si  i ≠ j , 1 si  i = j . {\displaystyle \delta _{ij}={\begin{cases}0&{\text{si }}i\neq j,\\1&{\text{si }}i=j.\...

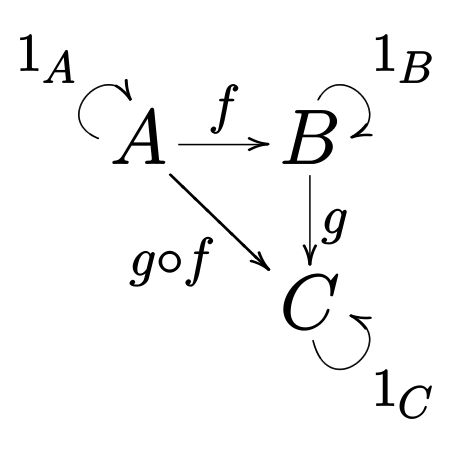
Mathematical object that generalizes the standard notions of sets and functions For other uses, see Category (disambiguation) § Mathematics. This is a category with a collection of objects A, B, C and collection of morphisms denoted f, g, g ∘ f, and the loops are the identity arrows. This category is typically denoted by a boldface 3. In mathematics, a category (sometimes called an abstract category to distinguish it from a concrete category) is a collection of objects that are linked...

Set of statistical processes for estimating the relationships among variables Regression line for 50 random points in a Gaussian distribution around the line y=1.5x+2 (not shown) Part of a series onRegression analysis Models Linear regression Simple regression Polynomial regression General linear model Generalized linear model Vector generalized linear model Discrete choice Binomial regression Binary regression Logistic regression Multinomial logistic regression Mixed logit Probit Multinomial...