Kleene's O
|
Read other articles:

Strada statale 613 Brindisi-LecceDenominazioni precedentiStrada a scorrimento veloce Brindisi-Lecce LocalizzazioneStato Italia Regioni Puglia DatiClassificazioneStrada statale InizioBrindisi FineLecce Lunghezza34,099[1] km Provvedimento di istituzioneD.M. 31/07/1970 - G.U. 282 del 07/11/1970[2] GestoreANAS (1970-) PercorsoStrade europee · Manuale La strada statale 613 Brindisi-Lecce (SS 613) o superstrada Brindisi-Lecce è una strada statale italiana il cui per...

Untuk pemeran Indonesia dengan nama yang sama, lihat Vanessa Angel (pemeran, lahir 1993). Vanessa AngelVanessa Angel pada 2009LahirVanessa Madeline Angel10 November 1966 (umur 57)London, InggrisPekerjaanPemeran, modelTahun aktif1985–kiniSuami/istriRick Otto (m. 1996; bercerai 2019)AnakIndia Otto Vanessa Madeline Angel (lahir 10 November 1966)[1] adalah seorang pemeran dan mantan model asal Inggris. Ia memerankan peran Lis...

Indian Earth observation satellite RISAT-2BR1RISAT-2BR1 with its Radial Rib Antenna in deployed configuration.NamesRadar Imaging Satellite-2BR1Mission typeEarth observationRadar imaging satelliteOperatorISROCOSPAR ID2019-089F SATCAT no.44857Websitehttps://www.isro.gov.in/Mission duration5 years (planned)4 years, 3 months and 28 days (in progress) Spacecraft propertiesSpacecraftRISAR-2BR1BusRISATManufacturerIndian Space Research OrganisationLaunch mass615 kg (1,356 lb)...

Human settlement in EnglandLittle BradleyLittle Bradley All SaintsLittle BradleyLocation within SuffolkPopulation60 DistrictWest SuffolkShire countySuffolkRegionEastCountryEnglandSovereign stateUnited KingdomPost townHaverhillPostcode districtCB9Dialling code01440UK ParliamentWest Suffolk List of places UK England Suffolk 52°08′N 0°27′E / 52.14°N 00.45°E / 52.14; 00.45 Little Bradley is a small village and civil parish in the West...

Michigan–Michigan State men's ice hockey rivalry Michigan Wolverines Michigan State Spartans First meetingJanuary 11, 1922Michigan 5, Michigan State 1[1]Latest meetingMarch 31, 2024Michigan 5, Michigan State 2TrophyThe Iron DStatisticsMeetings total343All-time seriesMichigan leads, 177–142–24[1]Largest victoryMichigan, 17–1 (1950)[1]Longest win streakMichigan, 19 (1928–1954)[1]Longest unbeaten streakMichigan, 33 (1928–1957)[1]Current win st...

This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (June 2017) (Learn how and when to remove this message) Prometheus Radio ProjectCompany typenon-profitIndustrylow power community radioFounded1998HeadquartersPhiladelphia, PennsylvaniaProductsLPFMWebsitePrometheus Radio Project The Prometheus Radio Project is a non-...
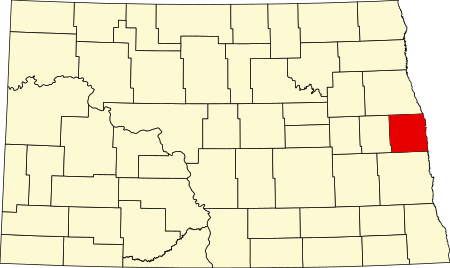
Pour les articles homonymes, voir Traill. Cet article est une ébauche concernant le Dakota du Nord. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Comté de TraillTraill County Le palais de justice de Hillsboro, siège du comté de Traill. Administration Pays États-Unis État Dakota du Nord Chef-lieu Hillsboro Démographie Population 7 997 hab. (2020) Densité 3,6 hab./km2 Géographie Coordonn�...
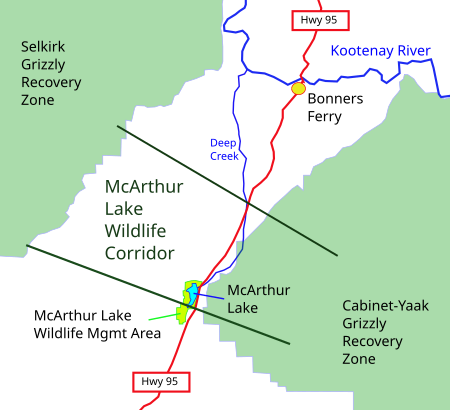
Combination of population genetics and landscape ecology Rivers and mountains can act as barriers to dispersal, thus preventing gene flow between populations. Landscape genetics is the scientific discipline that combines population genetics and landscape ecology. It broadly encompasses any study that analyses plant or animal population genetic data in conjunction with data on the landscape features and matrix quality where the sampled population lives. This allows for the analysis of mic...

National emblem of India State Emblem of IndiaArmiger Republic of IndiaAdopted26 January 1950ShieldLion Capital of AshokaMottoसत्यमेव जयते (Satyameva Jayate): Truth Alone Triumphs, from the Mundaka Upanishad, a part of Upanishads The State Emblem of India is the national emblem of the Republic of India and is used by the union government, many state governments, and other government agencies. The emblem is an adaptation of the Lion Capital of Ashoka, an ancient scul...

Bài viết hoặc đoạn này cần được wiki hóa để đáp ứng tiêu chuẩn quy cách định dạng và văn phong của Wikipedia. Xin hãy giúp sửa bài viết này bằng cách thêm bớt liên kết hoặc cải thiện bố cục và cách trình bày bài. Cục Du lịch Quốc gia Việt NamTên viết tắtVNATKhẩu hiệuViệt Nam - vẻ đẹp bất tậnThành lập27 tháng 6 năm 1978LoạiCơ quan nhà nước cấp CụcVị thế pháp lýHợp pháp, ho�...

1967 film by Andrew V. McLaglen This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Ballad of Josie – news · newspapers · books · scholar · JSTOR (February 2016) (Learn how and when to remove this message) The Ballad of JosieTheatrical release posterDirected byAndrew V. McLaglenWritten byHarold SwantonProduc...

Primera partición de Polonia Partición polaco-lituana de la Commonwealth después de la Primera Partición como protectorado del Imperio ruso (1773–1789)Pérdidas de poblaciónA Prusia 580 000[1]A Austria 2 650 000A Rusia 1 300 000Pérdidas territorialesA Prusia 36 000 km²A Austria 83 000 km²A Rusia 92 000 km² LocalizaciónPaís República de las Dos NacionesDatos generalesTipo aspecto de la historiaSuceso Primera reparto territorial...

State library Library of VirginiaThe Library of Virginia at its current locationLocationRichmond, Virginia, United States of AmericaTypeGovernment of VirginiaEstablished1823Other informationDirectorDennis T. Clark (as of January 25, 2024)Websitehttp://www.lva.virginia.gov/References: [1] The Library of Virginia in Richmond, Virginia, is the library agency of the Commonwealth of Virginia. It serves as the archival agency and the reference library for Virginia's seat of government. The ...

Presiden Republik Arab MesirPresiden StandarPetahanaAbdul Fattah as-Sisisejak 8 Juli 2014KediamanIstana Heliopolis, Kairo, MesirMasa jabatan4 tahunsatu kali masa jabatanPejabat perdanaMuhammad Naguib18 Juni 1953Situs webwww.presidency.gov.eg Halaman ini memuat daftar Presiden Mesir sejak terbentuk pada tahun 1953. Presiden adalah kepala negara Mesir dan panglima tertinggi Angkatan Bersenjata Mesir. Presiden yang menjabat saat ini adalah Abdul Fattah as-Sisi, sejak 8 Juli 2014. Latar Bela...

Strada statale 648del Valico di Monte ScuroDenominazioni precedentiStrada statale 107 Silana Crotonese Denominazioni successiveStrada provinciale 256 SS 648 di Montescuro LocalizzazioneStato Italia Regioni Calabria DatiClassificazioneStrada statale InizioSpezzano della Sila FineCamigliatello Silano Lunghezza23,520[1] km Provvedimento di istituzioneD.M. 133 del 14/03/1990 - G.U. 84 del 10/04/1990[2] GestoreANAS (1990-2002) Manuale La ex strada statale 648 del Valico d...

Second round of the 2019 Formula One season 2019 Bahrain Grand Prix Race 2 of 21 in the 2019 Formula One World Championship← Previous raceNext race → Race details[1]Date 31 March 2019Official name Formula 1 Gulf Air Bahrain Grand Prix 2019Location Bahrain International CircuitSakhir, BahrainCourse Permanent racing facilityCourse length 5.412 km (3.362 miles)Distance 57 laps, 308.238 km (191.530 miles)Weather ClearAttendance 97,000[2]Pole positionDriver ...
2013–14 FIS Cross-Country World CupDiscipline Men WomenOverall Martin Johnsrud Sundby Therese JohaugDistance Martin Johnsrud Sundby Therese JohaugSprint Ola Vigen Hattestad Kikkan RandallNations Cup Norway NorwayNations Cup Overall NorwayStage eventsNordic Opening Martin Johnsrud Sundby Marit BjørgenTour de Ski Martin Johnsrud Sundby Therese JohaugWorld Cup Final Martin Johnsrud Sundby Therese JohaugCompetitionLocations 15 venues 15 venuesIndividual 26 events 26 eventsRelay/Team 3 events ...

سفارة فيتنام في بولندا فيتنام بولندا الإحداثيات 52°10′25″N 21°04′02″E / 52.173536111111°N 21.0671°E / 52.173536111111; 21.0671 البلد بولندا المكان وارسو الاختصاص بولندا، وليتوانيا[1] الموقع الالكتروني الموقع الرسمي تعديل مصدري - تعديل سفارة فيتنام في بولندا هي أرفع تمث...

Location of Vienne in France Following is a list of senators of Vienne, people who have represented the department of Vienne in the Senate of France. Third Republic Senators for Vienne under the French Third Republic were:[1] Louis Olivier Bourbeau (1876–1877) Paul de Ladmirault (1876–1891) Eugène Arnaudeau (1877–1891) Louis de Beauchamp (1885–1891) Henri Salomon (1891–1900) Aristide Couteaux (1891–1906) Léopold Thézard (1891–1907) Célestin Contancin en 1900) Mauric...

Pedro Calungsod: Batang Martir (Journey of a Young Saint)SutradaraFrancis O. VillacortaDitulis olehFrancis O. VillacortaPemeranRocco NacinoChristian VazquezJestoni AlarconRyan EigenmannRobert CorreaVictor BasaMercedes CabralPenata musikNoel Diño EspenidaSinematograferDexter Dela PeñaSteven FlorRandy CuraPenyuntingTara IllenbergerPerusahaanproduksiWings EntertainmentDistributorHPI Synergy GroupTanggal rilis 25 Desember 2013 (2013-12-25) Durasi107 menitNegaraFilipinaBahasaFilipinaS...





































































