Hearing the shape of a drum
|
Read other articles:

Urutan kronofotografi tahun 1878 oleh Eadweard Muybridge tentang seekor kuda yang sedang bergerak Kuda dapat menggunakan berbagai lagak (pola gerakan kaki) selama bergerak melintasi tanah padat, baik secara alami maupun sebagai hasil pelatihan khusus yang dilakukan manusia. [1] Penggolongan Berjalan (Walk) Berjalan adalah lagak empat ketukan yang rata-rata mencapai 7 kilometer per jam (4,3 mph) . Saat berjalan, kaki kuda mengikuti urutan berikut: kaki belakang kiri, kaki kiri dep...

British reality game show franchise This article is about the franchise. For other uses, see The Circle (disambiguation). The CircleThe international logo for The CircleOriginal workThe CircleFilms and televisionTelevision seriesThe Circle (independent international versions, see below)AudioOriginal musicThe Circle Theme[1][2]MiscellaneousFirst aired18 September 2018 (2018-09-18)Distributor Channel 4 Netflix Official websitehttps://www.thecirclecasting.com/ The ...

Municipality in Cavite, Philippines This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Maragondon – news · newspapers · books · scholar · JSTOR (October 2021) (Learn how and when to remove this template message) Municipality in Calabarzon, PhilippinesMaragondonMunicipalityMunicipality of MaragondonMunicipal pla...

People's Revolutionary Government of the Republic of China redirects here. For the government of the People's Republic of China, see Government of the People's Republic of China. For other uses, see Government of China (disambiguation). Anti-Kuomintang government in Fujian, China 1933-1934 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fujian...

提示:此条目页的主题不是中華人民共和國最高領導人。 中华人民共和国 中华人民共和国政府与政治系列条目 执政党 中国共产党 党章、党旗党徽 主要负责人、领导核心 领导集体、民主集中制 意识形态、组织 以习近平同志为核心的党中央 两个维护、两个确立 全国代表大会 (二十大) 中央委员会 (二十届) 总书记:习近平 中央政治局 常务委员会 中央书记处 �...

Alessandro Crescenzi Informasi pribadiTanggal lahir 25 September 1991 (umur 32)Tempat lahir Roma, ItaliaTinggi 1,78 m (5 ft 10 in)Posisi bermain BekInformasi klubKlub saat ini Perugia (pinjaman dari Roma)Nomor 15Karier junior RomaKarier senior*Tahun Tim Tampil (Gol)2008– Roma 1 (0)2009–2010 → Grosseto (pinjaman) 6 (0)2010–2011 → Crotone (pinjaman) 33 (0)2011–2012 → Bari (pinjaman) 30 (0)2012 → Pescara (pinjaman) 1 (0)2013 → Novara (pinjaman) 20 (1)2013�...

NetherlandsFIBA zoneFIBA EuropeNational federationBasketball NederlandU20 European ChampionshipAppearances11Medals Bronze: 2 (2015, 2018)U20 European Championship Division BAppearances5Medals Gold: 1 (2009) Bronze: 1 (2023) The Netherlands women's national under-20 basketball team is a national basketball team of the Netherlands, administered by the Basketball Nederland.[1][2] It represents the country in women's international under-20 basketball competitions. FIBA U20 Women'...

Political party in Colombia This article is part of a series on thePolitics ofColombia Government Constitution of Colombia Law Taxation Policy Executive President Gustavo Petro (PH) Vice President Francia Márquez (PH) Cabinet of Colombia (Petro) Legislature Congress of Colombia Senate President of Senate Iván Name (AV) Chamber of Representatives President of the Chamber Andrés Calle (L) Judiciary Constitutional Court President of the Constitutional Court Cristina Pardo Supreme Court of Jui...

Chronologies Données clés 1799 1800 1801 1802 1803 1804 1805Décennies :1770 1780 1790 1800 1810 1820 1830Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égyp...

Edgar Mitchell Edgar Mitchell en 1971Información personalNombre de nacimiento Edgar Dean Mitchell Nombre en inglés Ed Mitchell Nacimiento 17 de septiembre de 1930 Hereford (Estados Unidos) Fallecimiento 4 de febrero de 2016 (85 años)West Palm Beach (Estados Unidos) Causa de muerte Cáncer de riñón Nacionalidad EstadounidenseEducaciónEducado en Escuela de Pilotos de Pruebas de la Fuerza Aérea de Estados UnidosAcademia Naval de los Estados UnidosArtesia High School (hasta 1948)Unive...

Dutch footballer This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Vito Wormgoor – news · newspapers · books · scholar · JSTOR (March 2017) (Learn how and when to remove this message) Vito Wormgoo...

Bay in Sydney Harbour, Sydney, New South Wales, Australia Blackwattle BayBlackwattle Bay Pontoon, GlebeBlackwattle BayLocationSydney Harbour, New South WalesCoordinates33°52′21″S 151°11′20″E / 33.872564°S 151.188912°E / -33.872564; 151.188912Part ofSydney HarbourPrimary outflowsJohnstons BayBasin countriesAustraliaSettlementsGlebe Blackwattle Bay is a bay located to the south–east of Glebe Island and east of Rozelle Bay on Sydney Harbour, in New...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (سبتمبر 2020) الدوري المصري الدرجة الرابعة تاريخ الإنشاء 1948 الرياضة كرة القدم البلد مصر القارة الكاف عدد الفرق 18 يتأهل...

تحتاج هذه المقالة إلى الاستشهاد بمصادر إضافية لتحسين وثوقيتها. فضلاً ساهم في تطوير هذه المقالة بإضافة استشهادات من مصادر موثوق بها. من الممكن التشكيك بالمعلومات غير المنسوبة إلى مصدر وإزالتها.جزء من سلسلة مقالات حولالنحو والتصريف في العربية الإعراب أقسام الكلام اسم فعل ح...
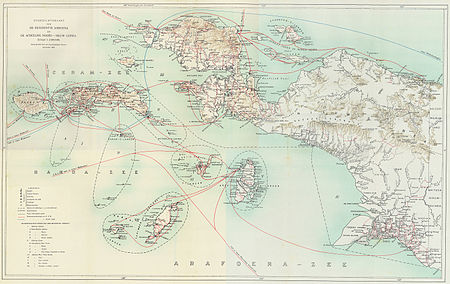
International conflict For the contemporary dispute, see Papua conflict. The disputed territory of West New Guinea The West New Guinea dispute (1950–1962), also known as the West Irian dispute, was a diplomatic and political conflict between the Netherlands and Indonesia over the territory of Dutch New Guinea. While the Netherlands had ceded sovereignty over most of the Dutch East Indies to Indonesia on 27 December 1949 following an independence struggle, it retained control over its colony...

American baseball player (1932–2023) Baseball player Ed BressoudBressoud with the Boston Red Sox in 1965ShortstopBorn: (1932-05-02)May 2, 1932Los Angeles, California, U.S.Died: July 13, 2023(2023-07-13) (aged 91)Walnut Creek, California, U.S.Batted: RightThrew: RightMLB debutJune 14, 1956, for the New York GiantsLast MLB appearanceSeptember 26, 1967, for the St. Louis CardinalsMLB statisticsBatting average.252Home runs94Runs batted in365 Teams New York / S...

For other people with similar names, see Latifur Rahman (disambiguation). Indian field hockey player Medal record Men's field hockey Olympic Games Representing India 1948 London Team Representing Pakistan 1956 Melbourne Team Latif-ur Rehman (1 January 1929 – 27 February 1987), also known as Latifur Rehman, was a field hockey player who competed internationally for India and Pakistan. He won a gold medal as a member of India's team at the 1948 Summer Olympics and a silver medal p...

Italian professional basketball player Giacomo DevecchiDevecchi with Dinamo in 2019No. 8 – Dinamo Basket SassariPositionSmall forward / shooting guardLeagueLBAPersonal informationBorn (1985-04-02) April 2, 1985 (age 39)Sant'Angelo Lodigiano, Lodi, ItalyNationalityItalianListed height1.96 m (6 ft 5 in)Listed weight88 kg (194 lb)Career informationPlaying career2001–presentCareer history2001–2004Olimpia Milano2004–2006Sutor Montegranaro2006–present...

Pour les articles homonymes, voir Makelele. Claude Makélélé Makélélé dans le staff du Paris Saint-Germain en 2013. Situation actuelle Équipe Asteras Tripolis (entraîneur) Biographie Nom Claude Makélélé Sinda Nationalité Congolaise Française (depuis 1992) Nat. sportive Française Naissance 18 février 1973 (51 ans) Kinshasa (Zaïre) Taille 1,74 m (5′ 9″) Période pro. 1992 – 2011 Poste Milieu défensif Pied fort Droit Parcours junior Années Club 1978-1989 US...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 2020 UEC European Track Championships – Women's madison – news · newspapers · books · scholar · JSTOR (November 2020) Women's madison at the 2020 UEC European Track ChampionshipsVenueKolodruma, PlovdivDate15 NovemberCompetitors16 from ...