Even and odd functions
|
Read other articles:

Hilton Fukuoka Sea Hawk dan Fukuoka Dome berada di Hawks Town. Hawks Town (ホークスタウンcode: ja is deprecated ) adalah kawasan perbelanjaan, olahraga, dan hiburan yang berintikan stadion bisbol Fukuoka Dome di Chūō-ku, Fukuoka, Jepang. Pengelola dan pemiliknya adalah Hawks Town Corporation, juga pengelola Hilton Fukuoka Sea Hawk dan Hawks Town Mall.[1] Lokasi Hawks Town berdekatan dengan Pantai Momochi, 15 menit berjalan kaki dari stasiun kereta bawah tanah Stasiun Tōjinma...

Military governor of Mari Ishtup-Ilum𒅖𒁾𒀭Military governor of MariStatue of Ishtup-Ilum.Reignc.2147–2136 BCEPredecessorNûr-MêrSuccessorIshgum-AdduDynastyShakkanakku dynasty Mariclass=notpageimage| Location of Mari, where Ishtup-Ilum ruled. Ishtup-Ilum, also Ishtup-El (𒅖𒁾𒀭, Ish-dub-ilum, c. 2147–2136 BCE)[1] was a ruler of the city of Mari, one of the military governors known as Shakkanakku in northern Mesopotamia, after the fall of the Akkadian Empire.[2]...

Castle in Ireland Bunratty CastleLocationBunratty village, County Clare, IrelandCoordinates52°41′48″N 8°48′42″W / 52.69667°N 8.81167°W / 52.69667; -8.81167Builtc. 1425Restored1956Restored by7th Viscount GortGoverning bodyClare County Council National monument of IrelandReference no.478[1] Location of Bunratty Castle in Ireland Bunratty Castle (Irish: Caisleán Bhun Raithe) is a large 15th-century tower house in County Clare, Ireland. It is loca...

Halaman ini berisi artikel tentang monarki Bahama. Untuk informasi tentang negara lainnya yang berbagi orang yang sama sebagai penguasa monarki, lihat Wilayah Persemakmuran. Ratu BahamaSedang berkuasaElizabeth II PerincianPewarisCharles, Pangeran WalesPenguasa pertamaElizabeth IIPembentukan10 Juli 1973 Monarki Bahama adalah sebuah sistem pemerintahan dimana seorang penguasa monarki pewaris menjadi pemimpin Persemakmuran Bahama. Penguasa monarki saat ininya adalah Ratu Elizabeth II,[1...

Daftar ini belum tentu lengkap. Anda dapat membantu Wikipedia dengan mengembangkannya. Berikut daftar tarian dari seluruh Indonesia berdasarkan abjad. Daftar mungkin belum lengkap. A Tari Andun Bengkulu Tari Angguk Yogyakarta Tari Angsa B Tari Badui Tari Baksa Kembang Tari Balean Dadas Tari Bali Tari Balumpa Tari Bambangan Cakil Tari Bangbarongan Tari Banjar Tari Banyumasan Tari Barongsai Tari Batu Nganga Tari Bedana Tari Bedhaya Tari Belian Tari Beksan Lawung Ageng Tari Bengberokan Tari Bida...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Astronomi radio – berita · surat kabar · buku · cendekiawan · JSTOR Sebuah teleskop radio diKompleks Goldstone DSC Astronomi radio adalah cabang astronomi yang mempelajari fenomena benda angkasa melalui ...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Double clôture électrifiée du camp Auschwitz I. Détail du monument antiguerre Mahnmal Bittermark (en), à Dortmund, Allemagne. Un camp de concentration est un lieu fermé de grande taille construit pour regrouper et pour détenir une population considérée comme ennemie, généralement dans de très mauvaises conditions de vie. Cette population peut se composer d'opposants politiques, de ressortissants de pays avec lesquels le pays d'accueil est en état de guerre, de groupes ethniq...
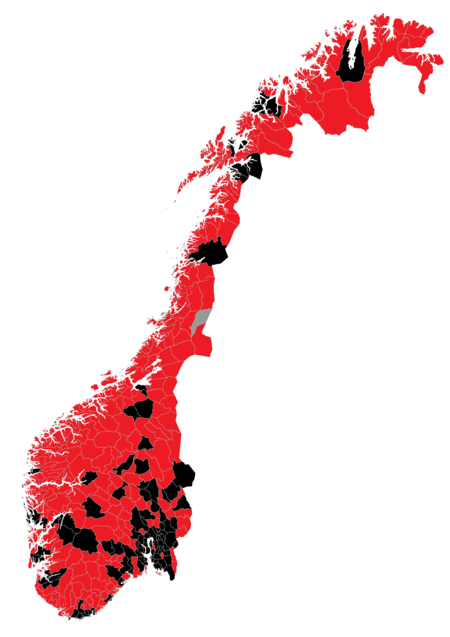
Pandemi koronavirus 2020 di NorwegiaPeta munisipalitas-munisipalitas dengan kasus koronavirus terkonfirmasi (merah) (pada 31 Maret)PenyakitCOVID-19Galur virusSARS-CoV-2LokasiNorwegiaKasus pertamaTromsøTanggal kemunculan26 Februari 2020(4 tahun, 1 bulan, 2 minggu dan 5 hari ago)AsalWuhan, Hubei, TiongkokKasus terkonfirmasi6.937[1]Kematian161[1] Pandemi koronavirus 2019–2020 dimulai di Norwegia pada 26 Februari 2020, dengan kasus berkembang pada bulan Mare...

This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Singuila – news · newspapers · books · scholar · JSTOR (June 2012) (Learn how and when to remove this message) You can help expand this article w...

American film and television screenwriter (1950–2015) Melissa MathisonMathison in 2015BornMelissa Marie Mathison[1](1950-06-03)June 3, 1950Los Angeles, California, U.S.DiedNovember 4, 2015(2015-11-04) (aged 65)Los Angeles, California, U.S.Alma materUniversity of California, BerkeleyOccupationScreenwriterYears active1979–2015Spouse Harrison Ford (m. 1983; div. 2004)Children2 Melissa Marie Mathison (June 3, 1950 – ...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Pour les articles homonymes, voir Sartre (homonymie). Maurice SartreMaurice Sartre en 2017.BiographieNaissance 3 octobre 1944 (79 ans)4e arrondissement de LyonNationalité françaiseActivité HistorienConjoint Annie Sartre-FauriatAutres informationsA travaillé pour Université de ToursDomaine histoire du Proche Orient antiqueMembre de Institut universitaire de FranceDistinctions Grand prix des Rendez-vous de l'histoire (2002)Prix Pierre-Lafue (2016)Chevalier des Arts et des Lettres (20...

This is a list of Sri Lanka Cricket lists, an article with a collection of lists relating to the Sri Lankan Cricket team. Teams Main article: List of Sri Lankan cricket teams Stadiums Main article: List of international cricket grounds in Sri Lanka Cricketers This section is empty. You can help by adding to it. (December 2022) Player statistics Batting List of international cricket centuries by Aravinda de Silva List of international cricket centuries by Kumar Sangakkara List of internationa...

This article is about the town in Alicante. For the municipality in Zaragoza, see La Joyosa. Not to be confused with Gioiosa. Municipality in Valencian Community, SpainVillajoyosaMunicipalityVillajoyosa/La Vila Joiosa FlagCoat of armsNickname: La VilaLocation of La Vila JoiosaVillajoyosaShow map of Valencian CommunityVillajoyosaShow map of SpainCoordinates: 38°30′19″N 0°13′58″W / 38.50528°N 0.23278°W / 38.50528; -0.23278Country SpainAutonomous com...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. اختراع آلة الطباعة قى القرن الخامس عشر الميلادي مع أطقم الحروف المحمولة بواسطة الألماني يوهان غوتنبرغ وهذا يعتبر الحدث الأكثر تأثيرا في العصر الحديث.[1] الجدول الزمني لل�...

Historical aspect of modern-day Khyber Pakhtunkhwa, Pakistan Map of the present-day Khyber Pakhtunkhwa province (green), previously the North-West Frontier; and FATA (purple)vteInstability on the North-West Frontier Afghan-Sikh Wars (1800–1837) Battle of Attock Battle of Multan Battle of Shopian Battle of Nowshera Battle of Jamrud First Afghan War to Second Sikh War (1838–48) First Anglo-Afghan War Sindh Campaign First Anglo-Sikh War Second Anglo-Sikh War Second Sikh War to Sepoy Revolt (...

此條目需要补充更多来源。 (2015年11月26日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:英國歷史 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 系列条目不列顛群島歷史 史前 早期英格兰 早期苏格兰 早期愛爾蘭 古代 鐵器�...

Family of all-terrain utility vehicles A John Deere Gator converted into an ambulance: This vehicle is owned by Toronto District St. John Ambulance. The John Deere Gator is a family of small all-terrain utility vehicles produced by the John Deere Corporation. Gators typically feature a box bed, similar in function to a pickup truck. The bed can also be installed as an electric dump body. The John Deere Gator has been made in a variety of configurations, with either four, five or six wheels.&#...







































![{\displaystyle [-A,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30ed42787a0511b07f6cc4622e0f6a812d39add)
















