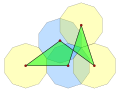
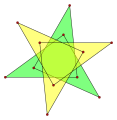
Density (polytope)
| |||||
Read other articles:

Pakuwon MallPakuwon Mall saat renovasi dan perluasan (2016)LokasiSurabaya, IndonesiaKoordinat7°17′22.5″S 112°40′30.4″E / 7.289583°S 112.675111°E / -7.289583; 112.675111Koordinat: 7°17′22.5″S 112°40′30.4″E / 7.289583°S 112.675111°E / -7.289583; 112.675111AlamatJalan Puncak Indah Lontar No.2Kelurahan Babatan, Kecamatan WiyungKota Surabaya, Jawa Timur 60227Tanggal dibuka8 November 2003 (Supermal Pakuwon Indah)13 November 200...

Chūichi NagumoLaksamana Madya Chuichi NagumoPengabdian Kekaisaran JepangDinas/cabangAngkatan Laut Kekaisaran JepangLama dinas1908-1944PangkatLaksamanaKesatuanKido ButaiKomandanKido Butai, Divisi I Kapal Induk, Armada Udara I, Armada III Angkatan Laut Kekaisaran Jepang, Distrik Angkatan Laut Sasebo, Distrik Angkatan Laut Kure, Armada I Angkatan Laut Jepang, Armada Kawasan Pasifik Tengah, Armada Udara 14 Angkatan Laut Kekaisaran Jepang[1]Perang/pertempuranPerang Dunia IIPertempura...

Concepción Cabrera de Armida Concepción Cabrera de Armida (8 Desember 1862 – 3 Maret 1937) adalah seorang penulis asal Meksiko. Ia lahir di San Luis Potosi, Meksiko dari pasangan Octaviano Cabrera Lacaveux dan Clara Arias Rivera sebagai anak ketujuh dari 12 bersaudara. Dua hari setelah lahir, ia dibaptis di Katedral San Juan de Dios. Pada 8 Desember 1872, ia menerima Sakramen Mahakudus. Ia berguru kepada para Suster Cinta Kasih (Hermanas de la Caridad). Pada 16 Januari 1876,...

Ada usul agar PT.Perkebunan II digabungkan ke artikel ini. (Diskusikan) Diusulkan sejak Maret 2022. PT Perkebunan Nusantara IILogo Perkebunan Nusantara IIJenisPerseroan terbatasIndustriPerkebunanNasibDigabung ke PTPN IPendahuluPT Perkebunan II (Persero)PT Perkebunan IX (Persero)Didirikan11 Maret 1996; 27 tahun lalu (1996-03-11)Ditutup03 Desember 2023 (2023-12-03)KantorpusatTanjung Morawa, Sumatera Utara, IndonesiaWilayah operasiSumatera Utara dan PapuaTokohkunciIrwan Perangin-angin&...

1808 painting by Jean-Auguste-Dominique Ingres The Valpinçon BatherArtistJean Auguste Dominique IngresYear1808MediumOil on canvasDimensions146 cm × 97.5 cm (57 in × 38.4 in)LocationLouvre, Paris The Valpinçon Bather (Fr: La Grande Baigneuse) is an 1808 painting by the French Neoclassical artist Jean-Auguste-Dominique Ingres (1780–1867), held in the Louvre since 1879. Painted while the artist was studying at the French Academy in Rome, it was ori...

Voce principale: Livorno. La Sala Moresca di villa Mimbelli Lista delle principali ville di Livorno, suddivise per località. Indice 1 Storia 2 Ville in città 3 Ville di Antignano 4 Ville di Ardenza 5 Ville di Montenero e dintorni 6 Ville di Monterotondo e dintorni 7 Ville di Quercianella e dintorni 8 Altre 9 Note 10 Bibliografia 11 Voci correlate 12 Altri progetti 13 Collegamenti esterni Storia Le ville di Livorno costituiscono un'importante testimonianza storica e architettonica della sto...

Latio redirects here. For the Nissan car model, see Nissan Latio. For the modern Italian administrative region, see Lazio. For other uses, see Latium (disambiguation). Historical region of Italy Latium and Campania Latium (/ˈleɪʃiəm/ LAY-shee-əm, US also /-ʃəm/ -shəm;[1][2][3][4] Latin: [ˈɫati.ũː]) is the region of central western Italy in which the city of Rome was founded and grew to be the capital city of the Roman Empire. Definiti...

Bandar Udara Radin Intan IIRadin Intan II AirportIATA: TKGICAO: WILLWMO: 96295InformasiJenisPublikPemilikPT Aviasi Pariwisata Indonesia (Persero)PengelolaPT Angkasa Pura IIMelayaniBalameka PringtataLokasiKabupaten Lampung Selatan, Lampung, IndonesiaZona waktuWIB (UTC+07:00)Ketinggian dpl86 mdplKoordinat05°14′33″S 105°10′44″E / 5.24250°S 105.17889°E / -5.24250; 105.17889Koordinat: 05°14′33″S 105°10′44″E / 5.24250°S 105.17...

Bacillus anthracis Foto mikrograf Bacillus anthracis dari kultur agar dengan pengecatan Fuchsin-biru metilen.PenyakitAntraks Pewarnaan GramGram-positif TaksonomiSuperdomainBiotaDomainBacteriaKerajaanBacillatiFilumBacillotaKelasBacilliOrdoCaryophanalesFamiliBacillaceaeGenusBacillusSpesiesBacillus anthracis lbs Bacillus anthracis merupakan spesies bakteri penyebab antraks—sebuah penyakit yang umum ditemukan pada hewan ternak dan terkadang pada manusia—dan satu-satunya patogen obligat pada g...

Pour les articles homonymes, voir Albert Ier. Albert von Thurn und Taxis Titre Chef de la Maison de Thurn und Taxis 2 juin 1885 – 22 janvier 1952(66 ans, 7 mois et 20 jours) Données clés Prédécesseur Maximilian Maria de Thurn und Taxis Successeur Francois-Joseph de Thurn und Taxis Biographie Titulature Prince de Thurn und TaxisPrince du Saint-Empire Dynastie Maison de Tour et Taxis Nom de naissance Albert Maria Joseph Maximilian Lamoral Fürst von Thurn und Taxis Na...

Voce principale: Calcio Lecco 1912. Associazione Calcio LeccoStagione 1952-1953Sport calcio Squadra Lecco Allenatore Hugo Lamanna Presidente Mario Ceppi IV Serie1º nel girone B, promosso in Serie C. Maggiori presenzeCampionato: Corradi (38) Miglior marcatoreCampionato: Bicicli, Vecchio (12) StadioStadio Mario Rigamonti 1951-1952 1953-1954 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Calcio Lecco nelle competizioni ufficiali d...

Stimulus package American Recovery and Reinvestment Act of 2009Long titleAn Act making supplemental appropriations for job preservation and creation, infrastructure investment, energy efficiency and science, assistance to the unemployed, State, and local fiscal stabilization, for the fiscal year ending September 30, 2009, and for other purposes.Acronyms (colloquial)ARRANicknamesRecovery ActEnacted bythe 111th United States CongressEffectiveFebruary 17, 2009CitationsPublic law111-5Statute...

Class of salt-tolerant archaea Halobacteria redirects here. For the genus, see Halobacterium. Haloarchaea Halobacterium sp. strain NRC-1, each cell about 5 µm in length. Scientific classification Domain: Archaea Kingdom: Euryarchaeota Phylum: Euryarchaeota Class: HalobacteriaGrant et al. 2002 Order Halobacteriales Haloferacales Natrialbales Synonyms Halomebacteria Cavalier-Smith 2002 Haloarchaea DasSarma and DasSarma 2008 Haloarchaea (halophilic archaea, halophilic archaebacteria, halobacter...

American author Jim Fergus Jim Fergus (born 1950) is an American author.[1] He has a degree in English from Colorado College and has worked as a tennis teacher and full-time freelance writer. His first novel was One Thousand White Women: The Journals of May Dodd,[2] which won the 1999 Fiction of the Year Award from the Mountains & Plains Booksellers Association and sold over one million copies in the United States.[citation needed] The French translation was on the...

Coppa Italia Serie C 2023-2024 Competizione Coppa Italia Serie C Sport Calcio Edizione 51ª Organizzatore Lega Italiana Calcio Professionistico Date dal 3 ottobre 2023al 2 aprile 2024 Luogo Italia Partecipanti 60 Risultati Vincitore Catania(1º titolo) Secondo Padova Semi-finalisti RiminiLucchese Statistiche Miglior marcatore Simone Palombi (5) Incontri disputati 62 Gol segnati 172 (2,77 per incontro) Cronologia della competizione 2022-2023 Manuale La Coppa Italia Ser...

Halland Hallands länDaerah di Swedia Lambang kebesaran NegaraSwediaIbu KotaHalmstadPemerintahan • GubernurLars-Erik Lövdén • Dewan KotaLandstinget HallandLuas • Total5.454 km2 (2,106 sq mi)Populasi (30 Juni 2014)[1] • Total308.735 • Kepadatan57/km2 (150/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)PDB NominalSEK 61,339 juta (2004)PDB per kapitaSEK 221.000NUTS RegionSE...

العلاقات البنينية التونسية بنين تونس بنين تونس تعديل مصدري - تعديل العلاقات البنينية التونسية هي العلاقات الثنائية التي تجمع بين بنين وتونس.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة بنين تونس المساح�...

Genre of music Not to be confused with New wave music. New-ageStylistic originsElectronicambientfolkworldclassicalkrautrockrockeasy listeningminimalprogressive rockCultural origins1960s and early 1970s, Europe and United StatesSubgenres Space music biomusic progressive electronic Neoclassical new-age music Fusion genresCeltic fusionOther topics New Age meditation environmentalism List of new-age music artists vaporwave New-age is a genre of music intended to create artistic inspiration, relax...

Altavilla Silentina Altavilla Silentina adalah sebuah kota dan Comune terletak di provinsi Salerno, Campania, sekitar 100 km selatan Naples, Italia. Altavilla Silentina tersebar pada dua punggung bukit. Hal ini terlindung di sisi timur laut oleh Pegunungan Alburni dan di Barat melihat dataran dari Sungai Sele dan Laut Tyrrhenian . Panorama termasuk pulau Capri, pegunungan dari Amalfi Coast dan Teluk Salerno di bagian utara. lbsKomune di Provinsi Salerno, CampaniaAcerno • Agropoli • A...

←→Декабрь Пн Вт Ср Чт Пт Сб Вс 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 2024 год Содержание 1 Праздники и памятные дни 1.1 Профессиональные 1.2 Религиозные 1.3 Именины 2 События 2.1 До XIX века 2.2 XIX век 2.3 XX век 2.4 XXI век 3 Родились 3.1 До XIX&#...