Complex random variable
|
Read other articles:

Pour un article plus général, voir Structure interne de la Terre. Cet article est une ébauche concernant la géologie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (janvier 2021). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qua...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Isabelle Berro-Lefèvre Hakim Mahkamah Eropa untuk Hak Asasi ManusiaMasa jabatan27 Juni 2006 – 1 Agustus 2015 Sunting kotak info • L • B Isabelle Berro-Lefèvre adalah seorang yuris (ahli hukum) asal Monako yang dikenal akan k...

Reaktor nuklir alam di Oklo: (1) Daerah reaktor nuklir. (2) Batu pasir. (3) Lapisan bijih uranium. (4) Granit. Oklo adalah sebuah daerah dekat kota Franceville, di provinsi Haut-Ogooué, negara Gabon, yang terletak di Afrika Tengah. Beberapa reaktor nuklir alam ditemukan dalam daerah pertambangan uranium pada tahun 1972. Sejarah Gabon merupakan koloni Prancis ketika para prospektor dari komisariat energi nuklir Prancis (bagian industri, kemudian menjadi COGEMA dan terakhir sebagai Areva NC) m...

Historic building in Houston, Texas, U.S. United States historic placeHogg BuildingU.S. National Register of Historic PlacesRecorded Texas Historic Landmark The building's exterior in 2011Show map of Houston DowntownShow map of TexasShow map of the United StatesLocation401 Louisiana Street, Houston, TexasCoordinates29°45′45″N 95°21′50″W / 29.76250°N 95.36389°W / 29.76250; -95.36389Arealess than one acreBuilt1921 (1921)ArchitectBarglebaugh & Whitson...

Sumber referensi dari artikel ini belum dipastikan dan mungkin isinya tidak benar. Mohon periksa, kembangkan artikel ini, dan tambahkan sumber yang benar pada bagian yang diperlukan. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari s...

العلاقات البحرينية الفانواتية البحرين فانواتو البحرين فانواتو تعديل مصدري - تعديل العلاقات البحرينية الفانواتية هي العلاقات الثنائية التي تجمع بين البحرين وفانواتو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ...

The bishop-fish, from Poland in the 16th century Lists of humanoids cover humanoids, imaginary species similar to humans. They are organized by type (avian, piscine and amphibian, reptilian, and extraterrestrial), and by medium (literature, comics, animation, television, film and video games). By type List of avian humanoids List of piscine and amphibian humanoids List of reptilian humanoids List of humanoid aliens Little people (mythology) By medium List of fictional humanoid species in lit...

ShkharaTitik tertinggiKetinggian5.203 m (17.070 ft)[1][2]Puncak1.357 m (4.452 ft)Masuk dalam daftarTujuh Puncak KetigaTitik tertinggi negaraKoordinat43°00′02″N 43°06′44″E / 43.00056°N 43.11222°E / 43.00056; 43.11222Koordinat: 43°00′02″N 43°06′44″E / 43.00056°N 43.11222°E / 43.00056; 43.11222 GeografiShkharaLokasi Shkhara di pegunungan KaukasusLetakShkhara, Svaneti, GeorgiaNegaraGe...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

American restaurant chain This article is about the American restaurant chain. For other uses, see Waffle House (disambiguation). Waffle HouseTrade nameWaffle HouseCompany typePrivateIndustryRestaurantsGenreCasual diningFoundedSeptember 5, 1955; 68 years ago (1955-09-05)Avondale Estates, Georgia, United StatesFoundersJoe RogersTom ForknerHeadquarters5986 Financial Drive, Norcross, Georgia, United StatesNumber of locations1,973[1]Area served25 U.S. statesKey peopleWal...

Town in New Hampshire, United States Town in New Hampshire, United StatesCanterbury, New HampshireTownTown center: Canterbury United Community Church (L) & Country Store (R) SealLocation in Merrimack County and the state of New HampshireCoordinates: 43°20′11″N 71°33′53″W / 43.33639°N 71.56472°W / 43.33639; -71.56472CountryUnited StatesStateNew HampshireCountyMerrimackIncorporated1741VillagesCanterburyCanterbury StationShaker VillageGovernment ...

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

Association football club in England Football clubBrantham AthleticFull nameBrantham Athletic Football ClubNickname(s)The Blue ImpsFounded1887GroundBrantham Leisure Centre, BranthamCapacity1,200 (200 seated)[1]ChairmanPeter CrowhurstManagerPip BoylandLeagueEastern Counties League Premier Division2022–23Eastern Counties League Premier Division, 13th of 20WebsiteClub website Home colours Away colours Brantham's home ground Brantham Athletic Football Club is a football club based in Br...

Fourth Division 1961-1962 Competizione Fourth Division Sport Calcio Edizione 4ª Organizzatore Football League Date dal 19 agosto 1961al 3 maggio 1962 Luogo Inghilterra Galles Partecipanti 24 Formula girone all'italiana A/R Risultati Vincitore Millwall(1º titolo) Altre promozioni Carlisle UnitedColchester UnitedWrexham Statistiche Miglior marcatore Bobby Hunt (37) Incontri disputati 506 Gol segnati 1 690 (3,34 per incontro) Cronologia della competizione 196...

Mercedes-Benz W114/W1151973 Mercedes-Benz 220DInformasiProdusenMercedes-BenzJuga disebutMercedes-Benz Strich-Acht (Jerman)Mercy Mini (Indonesia)Masa produksi1968–19761,919,056 unitSedan: 1,852,008Coupé: 67,048PerakitanStuttgart, Jerman BaratBremen, Jerman BaratSindelfingen, Jerman BaratEast London, Afrika SelatanSetúbal, Portugal (Movauto)Barcelona, Venezuela (CKD)González Catán, ArgentinaPerancangPaul BracqBodi & rangkaKelasmobil Eksekutif (E)Grand tourer (W114/W115 Coupé...

Legendary creature in Danish, Frisian and German mythology Nis Puk in the legendary forest on Sylt Statue of Nis Puk in Neukirchen/Nykirke The Nis Puk[1] (sometimes also Niß Puk,[2] in Danish also Nis Pug(e)[3]) is a legendary creature, a kind of Kobold, from Danish-[1][4][5], Low German-[6] and North Frisian-speaking[7] areas of Northern Germany[6] and Southern Denmark,[8] among them Schleswig, today divided int...

Defunct flying squadron of the Royal Air Force No. 543 Squadron RAFSquadron badgeActive19 October 1942 – 18 October 1943 24 September 1955 – 24 May 1974Country United KingdomBranch Royal Air ForceRolePhotographic ReconnaissancePart ofNo. 16 Group, RAF Coastal Command (42–43)[1] No. 3 Group, RAF Bomber Command (55–68)[2] No. 1 Group, RAF Strike Command (68–74)[3]Motto(s)Valiant and Vigilant[4][5]InsigniaSquadron Badge heraldryA crane's hea...

2017 South American Youth Football ChampionshipCampeonato Sudamericano Sub-20“Juventud de America” Ecuador 2017Tournament detailsHost countryEcuadorDates18 January – 11 FebruaryTeams10 (from 1 confederation)Venue(s)4 (in 4 host cities)Final positionsChampions Uruguay (8th title)Runners-up EcuadorThird place VenezuelaFourth place ArgentinaTournament statisticsMatches played35Goals scored91 (2.6 per match)Top scorer(s) Rodrigo Amaral Bryan Cabezas L...

English footballer Lewis Dobbin Dobbin playing for England U17 in 2019Personal informationFull name Lewis Norman DobbinDate of birth (2003-01-03) 3 January 2003 (age 21)[1]Place of birth Stoke-on-Trent, EnglandHeight 1.75 m (5 ft 9 in)[1]Position(s) WingerTeam informationCurrent team Aston VillaYouth career2014−2021 EvertonSenior career*Years Team Apps (Gls)2021–2024 Everton 15 (1)2022–2023 → Derby County (loan) 43 (3)2024– Aston Villa 0 (0)Intern...

Czech composer (1841–1904) Antonín DvořákDvořák in 1882Born(1841-09-08)8 September 1841Nelahozeves, Austrian EmpireDied1 May 1904(1904-05-01) (aged 62)Vysoká u Příbramě, Austria-HungaryWorksList of compositions by Antonín Dvořák Antonín Leopold Dvořák (/d(ə)ˈvɔːrʒɑːk, -ʒæk/ d(ə-)VOR-zha(h)k; Czech: [ˈantoɲiːn ˈlɛopold ˈdvor̝aːk] ⓘ; 8 September 1841 – 1 May 1904) was a Czech composer. He frequently employed rhythms and other aspects of the fo...














![{\displaystyle \operatorname {E} [Z]={\frac {1}{4}}(1+i)+{\frac {1}{4}}(1-i)+{\frac {1}{2}}2={\frac {3}{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c524ba54cdf76d00057ff202c9ef13d276797808)

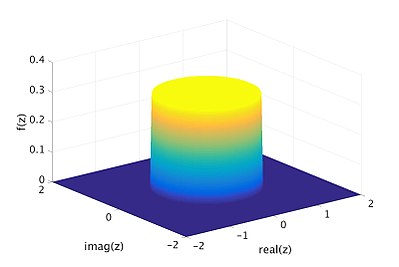



![{\displaystyle F_{Z}:\mathbb {C} \to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a49f4f55d06b18465dbc269884ebf7747b9156f3)







![{\displaystyle \operatorname {E} [Z]=\operatorname {E} [\Re {(Z)}]+i\operatorname {E} [\Im {(Z)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e1ff26c4d56190d3bcbbc0f5aaede2132ea4de)
![{\displaystyle \operatorname {E} [\Re {(Z)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e844e16f165052318326c84418f6f397eef22c61)
![{\displaystyle \operatorname {E} [\Im {(Z)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db17b20ce3199ef25f805f27c8473a08d3753378)

![{\displaystyle \operatorname {E} [Z]=\iint _{\mathbb {C} }z\cdot f_{Z}(z)\,dx\,dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce36d7e5aca36e4baed05d1ce7eb8be351a3da68)

![{\displaystyle \operatorname {E} [Z]=\sum _{z\in \mathbb {Z} }z\cdot p_{Z}(z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bd6feced28ac4cb07956d41e9b0476422f8b168)
![{\displaystyle {\overline {\operatorname {E} [Z]}}=\operatorname {E} [{\overline {Z}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0f389d24b8d094d5cbcfe0587f73462936d18ff)
![{\displaystyle \operatorname {E} [\cdot ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a71518eb57ffaf54c0c31bf94de5ac9d7ab11a1)
![{\displaystyle \operatorname {E} [aZ+bW]=a\operatorname {E} [Z]+b\operatorname {E} [W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e642bbe3e97314e03a0804a0bcfeaaf4a49c7bc)


![{\displaystyle \operatorname {K} _{ZZ}=\operatorname {Var} [Z]=\operatorname {E} \left[\left|Z-\operatorname {E} [Z]\right|^{2}\right]=\operatorname {E} [|Z|^{2}]-\left|\operatorname {E} [Z]\right|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20d080a97d05f3891fad48566952956c8bc33616)
![{\displaystyle \operatorname {Var} [Z]=\operatorname {Var} [\Re {(Z)}]+\operatorname {Var} [\Im {(Z)}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/add16b3176754caaa4cf67a75a16b4ac92b34c76)
![{\displaystyle \operatorname {Var} \left[\sum _{k=1}^{N}a_{k}Z_{k}\right]=\sum _{i=1}^{N}\sum _{j=1}^{N}a_{i}{\overline {a_{j}}}\operatorname {Cov} [Z_{i},Z_{j}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f99e419701670b4886082740417b566f5c3f3123)
![{\displaystyle \operatorname {J} _{ZZ}=\operatorname {E} [(Z-\operatorname {E} [Z])^{2}]=\operatorname {E} [Z^{2}]-(\operatorname {E} [Z])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ff6bdd87afbafd84fa355854e5d4d7884b7cb5f)

![{\displaystyle {\begin{bmatrix}\operatorname {Var} [\Re {(Z)}]&\operatorname {Cov} [\Im {(Z)},\Re {(Z)}]\\\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]&\operatorname {Var} [\Im {(Z)}]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac330d152bea21f53db8f3ff194d894157b6fc3c)
![{\displaystyle \operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=\operatorname {Cov} [\Im {(Z)},\Re {(Z)}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c2fd64c83c920bd9f44dfcb5281682245f7d103)
![{\displaystyle {\begin{aligned}&\operatorname {Var} [\Re {(Z)}]={\tfrac {1}{2}}\operatorname {Re} (\operatorname {K} _{ZZ}+\operatorname {J} _{ZZ})\\&\operatorname {Var} [\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Re} (\operatorname {K} _{ZZ}-\operatorname {J} _{ZZ})\\&\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Im} (\operatorname {J} _{ZZ})\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/660a39d44691cd1f64d313944c0046eeaa5fe2cc)
![{\displaystyle {\begin{aligned}&\operatorname {K} _{ZZ}=\operatorname {Var} [\Re {(Z)}]+\operatorname {Var} [\Im {(Z)}]\\&\operatorname {J} _{ZZ}=\operatorname {Var} [\Re {(Z)}]-\operatorname {Var} [\Im {(Z)}]+i2\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82090510b637bbd7629cffdef53b712e564ec908)

![{\displaystyle \operatorname {K} _{ZW}=\operatorname {Cov} [Z,W]=\operatorname {E} [(Z-\operatorname {E} [Z]){\overline {(W-\operatorname {E} [W])}}]=\operatorname {E} [Z{\overline {W}}]-\operatorname {E} [Z]\operatorname {E} [{\overline {W}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a961696e5eb2780adc679459b7cf2c5000dd1e)
![{\displaystyle \operatorname {J} _{ZW}=\operatorname {Cov} [Z,{\overline {W}}]=\operatorname {E} [(Z-\operatorname {E} [Z])(W-\operatorname {E} [W])]=\operatorname {E} [ZW]-\operatorname {E} [Z]\operatorname {E} [W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0850e20d08a280f61bd0e8db2c108656c09f163)
![{\displaystyle \operatorname {Cov} [Z,W]={\overline {\operatorname {Cov} [W,Z]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6c45f52a23a45d8c0489113054f2899fc7abe05)
![{\displaystyle \operatorname {Cov} [\alpha Z,W]=\alpha \operatorname {Cov} [Z,W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36d563b3f4a69e63da7c74774262faa56e9d8dbb)
![{\displaystyle \operatorname {Cov} [Z,\alpha W]={\overline {\alpha }}\operatorname {Cov} [Z,W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdae2df03771a6783a07fce94daafe717183d542)
![{\displaystyle \operatorname {Cov} [Z_{1}+Z_{2},W]=\operatorname {Cov} [Z_{1},W]+\operatorname {Cov} [Z_{2},W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58046998dba3171529973d2cea6df46bd55cd24b)
![{\displaystyle \operatorname {Cov} [Z,W_{1}+W_{2}]=\operatorname {Cov} [Z,W_{1}]+\operatorname {Cov} [Z,W_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21ba4eef59808fe6d651f74824fa7354b63de613)
![{\displaystyle \operatorname {Cov} [Z,Z]={\operatorname {Var} [Z]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d0dd5a038210af5d291b2baf8d6f5f4017130ba)

![{\displaystyle \operatorname {E} [Z{\overline {W}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9158c9d3364ee6a00a491d275b5aaa59fb06b08)
![{\displaystyle \phi \in [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd67c7af835707a32f70e8ceb8388953705d2ab3)

![{\displaystyle \operatorname {E} [Z]=\operatorname {E} [e^{\mathrm {i} \phi }Z]=e^{\mathrm {i} \phi }\operatorname {E} [Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a0c0eaaf719d6a7f539ee634a8ada78a25fb814)

![{\displaystyle \operatorname {E} [ZZ]=\operatorname {E} [e^{\mathrm {i} \phi }Ze^{\mathrm {i} \phi }Z]=e^{\mathrm {2} i\phi }\operatorname {E} [ZZ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d399819a5ae5dbfd8d504a1771a23da9424712fe)
![{\displaystyle [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)
![{\displaystyle \operatorname {E} [Z]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6c80bd7c75894b696a91f03059d601eed06827f)
![{\displaystyle \operatorname {Var} [Z]<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9598b3723f10a6af6b01d1a9e70dac49eaa054e)
![{\displaystyle \operatorname {E} [Z^{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0142e4405a348fd70966a8f62d4c260f5b30498)
![{\displaystyle \operatorname {E} [\Re {(Z)}^{2}]=\operatorname {E} [\Im {(Z)}^{2}]\neq \infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a24c7509a56aab23c94a541282cc12c0f2793e70)
![{\displaystyle \operatorname {E} [\Re {(Z)}\Im {(Z)}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38f594a6d61e9568109957798cff69ca1239516b)
![{\displaystyle {\begin{bmatrix}{\frac {1}{2}}\operatorname {Var} [Z]&0\\0&{\frac {1}{2}}\operatorname {Var} [Z]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/409bedd03d9fcbd63fb8d7338d6dc4ad4fe69e86)
![{\displaystyle {\begin{aligned}&\operatorname {Var} [\Re {(Z)}]=\operatorname {Var} [\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Var} [Z]\\&\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=0\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cc188b8b1273b1a3c41d381002ba1095ce961ec)
![{\displaystyle \left|\operatorname {E} \left[Z{\overline {W}}\right]\right|^{2}\leq \left|\operatorname {E} \left[\left|Z{\overline {W}}\right|\right]\right|^{2}\leq \operatorname {E} \left[|Z|^{2}\right]\operatorname {E} \left[|W|^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d22338d330f3e5c32c1fb25b14de2d80569cac86)

![{\displaystyle \varphi _{Z}(\omega )=\operatorname {E} \left[e^{i\Re {({\overline {\omega }}Z)}}\right]=\operatorname {E} \left[e^{i(\Re {(\omega )}\Re {(Z)}+\Im {(\omega )}\Im {(Z)})}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88cf0381ac2f47d34cdf5a23923e0699a8b6515d)