Bernoulli distribution

Probability mass function Three examples of Bernoulli distribution:   ${\displaystyle P(x=0)=0{.}2}$ and ${\displaystyle P(x=1)=0{.}8}$   ${\displaystyle P(x=0)=0{.}8}$ and ${\displaystyle P(x=1)=0{.}2}$   ${\displaystyle P(x=0)=0{.}5}$ and ${\displaystyle P(x=1)=0{.}5}$
Parameters	${\displaystyle 0\leq p\leq 1}$ ${\displaystyle q=1-p}$
Support	${\displaystyle k\in \{0,1\}}$
PMF	${\displaystyle {\begin{cases}q=1-p&{\text{if }}k=0\\p&{\text{if }}k=1\end{cases}}}$
CDF	${\displaystyle {\begin{cases}0&{\text{if }}k<0\\1-p&{\text{if }}0\leq k<1\\1&{\text{if }}k\geq 1\end{cases}}}$
Mean	${\displaystyle p}$
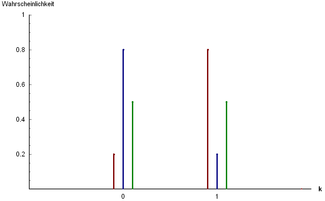
Median	${\displaystyle {\begin{cases}0&{\text{if }}p<1/2\\\left[0,1\right]&{\text{if }}p=1/2\\1&{\text{if }}p>1/2\end{cases}}}$
Mode	${\displaystyle {\begin{cases}0&{\text{if }}p<1/2\\0,1&{\text{if }}p=1/2\\1&{\text{if }}p>1/2\end{cases}}}$
Variance	${\displaystyle p(1-p)=pq}$
MAD	${\displaystyle 2p(1-p)=2pq}$
Skewness	${\displaystyle {\frac {q-p}{\sqrt {pq}}}}$
Excess kurtosis	${\displaystyle {\frac {1-6pq}{pq}}}$
Entropy	${\displaystyle -q\ln q-p\ln p}$
MGF	${\displaystyle q+pe^{t}}$
CF	${\displaystyle q+pe^{it}}$
PGF	${\displaystyle q+pz}$
Fisher information	${\displaystyle {\frac {1}{pq}}}$

Part of a series on statistics
Probability theory
Probability Axioms Determinism System Indeterminism Randomness
Probability space Sample space Event Collectively exhaustive events Elementary event Mutual exclusivity Outcome Singleton Experiment Bernoulli trial Probability distribution Bernoulli distribution Binomial distribution Exponential distribution Normal distribution Pareto distribution Poisson distribution Probability measure Random variable Bernoulli process Continuous or discrete Expected value Variance Markov chain Observed value Random walk Stochastic process
Complementary event Joint probability Marginal probability Conditional probability
Independence Conditional independence Law of total probability Law of large numbers Bayes' theorem Boole's inequality
Venn diagram Tree diagram
v t e

In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,^[1] is the discrete probability distribution of a random variable which takes the value 1 with probability ${\displaystyle p}$ and the value 0 with probability ${\displaystyle q=1-p}$. Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes–no question. Such questions lead to outcomes that are Boolean-valued: a single bit whose value is success/yes/true/one with probability p and failure/no/false/zero with probability q. It can be used to represent a (possibly biased) coin toss where 1 and 0 would represent "heads" and "tails", respectively, and p would be the probability of the coin landing on heads (or vice versa where 1 would represent tails and p would be the probability of tails). In particular, unfair coins would have ${\displaystyle p\neq 1/2.}$

The Bernoulli distribution is a special case of the binomial distribution where a single trial is conducted (so n would be 1 for such a binomial distribution). It is also a special case of the two-point distribution, for which the possible outcomes need not be 0 and 1. ^[2]

If ${\displaystyle X}$ is a random variable with a Bernoulli distribution, then:

${\displaystyle \Pr(X=1)=p=1-\Pr(X=0)=1-q.}$

The probability mass function ${\displaystyle f}$ of this distribution, over possible outcomes k, is

${\displaystyle f(k;p)={\begin{cases}p&{\text{if }}k=1,\\q=1-p&{\text{if }}k=0.\end{cases}}}$^[3]

This can also be expressed as

${\displaystyle f(k;p)=p^{k}(1-p)^{1-k}\quad {\text{for }}k\in \{0,1\}}$

or as

${\displaystyle f(k;p)=pk+(1-p)(1-k)\quad {\text{for }}k\in \{0,1\}.}$

The Bernoulli distribution is a special case of the binomial distribution with ${\displaystyle n=1.}$^[4]

The kurtosis goes to infinity for high and low values of ${\displaystyle p,}$ but for ${\displaystyle p=1/2}$ the two-point distributions including the Bernoulli distribution have a lower excess kurtosis, namely −2, than any other probability distribution.

The Bernoulli distributions for ${\displaystyle 0\leq p\leq 1}$ form an exponential family.

The maximum likelihood estimator of ${\displaystyle p}$ based on a random sample is the sample mean.

The expected value of a Bernoulli random variable ${\displaystyle X}$ is

${\displaystyle \operatorname {E} [X]=p}$

This is due to the fact that for a Bernoulli distributed random variable ${\displaystyle X}$ with ${\displaystyle \Pr(X=1)=p}$ and ${\displaystyle \Pr(X=0)=q}$ we find

${\displaystyle \operatorname {E} [X]=\Pr(X=1)\cdot 1+\Pr(X=0)\cdot 0=p\cdot 1+q\cdot 0=p.}$^[3]

The variance of a Bernoulli distributed ${\displaystyle X}$ is

${\displaystyle \operatorname {Var} [X]=pq=p(1-p)}$

We first find

${\displaystyle \operatorname {E} [X^{2}]=\Pr(X=1)\cdot 1^{2}+\Pr(X=0)\cdot 0^{2}}$

${\displaystyle =p\cdot 1^{2}+q\cdot 0^{2}=p=\operatorname {E} [X]}$

From this follows

${\displaystyle \operatorname {Var} [X]=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}=\operatorname {E} [X]-\operatorname {E} [X]^{2}}$

${\displaystyle =p-p^{2}=p(1-p)=pq}$^[3]

With this result it is easy to prove that, for any Bernoulli distribution, its variance will have a value inside ${\displaystyle [0,1/4]}$.

The skewness is ${\displaystyle {\frac {q-p}{\sqrt {pq}}}={\frac {1-2p}{\sqrt {pq}}}}$. When we take the standardized Bernoulli distributed random variable ${\displaystyle {\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}}$ we find that this random variable attains ${\displaystyle {\frac {q}{\sqrt {pq}}}}$ with probability ${\displaystyle p}$ and attains ${\displaystyle -{\frac {p}{\sqrt {pq}}}}$ with probability ${\displaystyle q}$. Thus we get

${\displaystyle {\begin{aligned}\gamma _{1}&=\operatorname {E} \left[\left({\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}\right)^{3}\right]\\&=p\cdot \left({\frac {q}{\sqrt {pq}}}\right)^{3}+q\cdot \left(-{\frac {p}{\sqrt {pq}}}\right)^{3}\\&={\frac {1}{{\sqrt {pq}}^{3}}}\left(pq^{3}-qp^{3}\right)\\&={\frac {pq}{{\sqrt {pq}}^{3}}}(q^{2}-p^{2})\\&={\frac {(1-p)^{2}-p^{2}}{\sqrt {pq}}}\\&={\frac {1-2p}{\sqrt {pq}}}={\frac {q-p}{\sqrt {pq}}}.\end{aligned}}}$

The raw moments are all equal due to the fact that ${\displaystyle 1^{k}=1}$ and ${\displaystyle 0^{k}=0}$.

${\displaystyle \operatorname {E} [X^{k}]=\Pr(X=1)\cdot 1^{k}+\Pr(X=0)\cdot 0^{k}=p\cdot 1+q\cdot 0=p=\operatorname {E} [X].}$

The central moment of order ${\displaystyle k}$ is given by

${\displaystyle \mu _{k}=(1-p)(-p)^{k}+p(1-p)^{k}.}$

The first six central moments are

${\displaystyle {\begin{aligned}\mu _{1}&=0,\\\mu _{2}&=p(1-p),\\\mu _{3}&=p(1-p)(1-2p),\\\mu _{4}&=p(1-p)(1-3p(1-p)),\\\mu _{5}&=p(1-p)(1-2p)(1-2p(1-p)),\\\mu _{6}&=p(1-p)(1-5p(1-p)(1-p(1-p))).\end{aligned}}}$

The higher central moments can be expressed more compactly in terms of ${\displaystyle \mu _{2}}$ and ${\displaystyle \mu _{3}}$

${\displaystyle {\begin{aligned}\mu _{4}&=\mu _{2}(1-3\mu _{2}),\\\mu _{5}&=\mu _{3}(1-2\mu _{2}),\\\mu _{6}&=\mu _{2}(1-5\mu _{2}(1-\mu _{2})).\end{aligned}}}$

The first six cumulants are

${\displaystyle {\begin{aligned}\kappa _{1}&=p,\\\kappa _{2}&=\mu _{2},\\\kappa _{3}&=\mu _{3},\\\kappa _{4}&=\mu _{2}(1-6\mu _{2}),\\\kappa _{5}&=\mu _{3}(1-12\mu _{2}),\\\kappa _{6}&=\mu _{2}(1-30\mu _{2}(1-4\mu _{2})).\end{aligned}}}$

Entropy is a measure of uncertainty or randomness in a probability distribution. For a Bernoulli random variable ${\displaystyle X}$ with success probability ${\displaystyle p}$ and failure probability ${\displaystyle q=1-p}$, the entropy ${\displaystyle H(X)}$ is defined as:

${\displaystyle {\begin{aligned}H(X)&=\mathbb {E} _{p}\ln({\frac {1}{P(X)}})=-[P(X=0)\ln P(X=0)+P(X=1)\ln P(X=1)]\\H(X)&=-(q\ln q+p\ln p),\quad q=P(X=0),p=P(X=1)\end{aligned}}}$

The entropy is maximized when ${\displaystyle p=0.5}$, indicating the highest level of uncertainty when both outcomes are equally likely. The entropy is zero when ${\displaystyle p=0}$ or ${\displaystyle p=1}$, where one outcome is certain.

Fisher information measures the amount of information that an observable random variable ${\displaystyle X}$ carries about an unknown parameter ${\displaystyle p}$ upon which the probability of ${\displaystyle X}$ depends. For the Bernoulli distribution, the Fisher information with respect to the parameter ${\displaystyle p}$ is given by:

${\displaystyle {\begin{aligned}I(p)={\frac {1}{pq}}\end{aligned}}}$

Proof:

• The Likelihood Function for a Bernoulli random variable${\displaystyle X}$ is:

${\displaystyle {\begin{aligned}L(p;X)=p^{X}(1-p)^{1-X}\end{aligned}}}$

This represents the probability of observing ${\displaystyle X}$ given the parameter ${\displaystyle p}$.

• The Log-Likelihood Function is:

${\displaystyle {\begin{aligned}\ln L(p;X)=X\ln p+(1-X)\ln(1-p)\end{aligned}}}$

• The Score Function (the first derivative of the log-likelihood w.r.t. ${\displaystyle p}$ is:

${\displaystyle {\begin{aligned}{\frac {\partial }{\partial p}}\ln L(p;X)={\frac {X}{p}}-{\frac {1-X}{1-p}}\end{aligned}}}$

• The second derivative of the log-likelihood function is:

${\displaystyle {\begin{aligned}{\frac {\partial ^{2}}{\partial p^{2}}}\ln L(p;X)=-{\frac {X}{p^{2}}}-{\frac {1-X}{(1-p)^{2}}}\end{aligned}}}$

• Fisher information is calculated as the negative expected value of the second derivative of the log-likelihood:

${\displaystyle {\begin{aligned}I(p)=-E\left[{\frac {\partial ^{2}}{\partial p^{2}}}\ln L(p;X)\right]=-\left(-{\frac {p}{p^{2}}}-{\frac {1-p}{(1-p)^{2}}}\right)={\frac {1}{p(1-p)}}={\frac {1}{pq}}\end{aligned}}}$

It is maximized when ${\displaystyle p=0.5}$, reflecting maximum uncertainty and thus maximum information about the parameter ${\displaystyle p}$.

• If ${\displaystyle X_{1},\dots ,X_{n}}$ are independent, identically distributed (i.i.d.) random variables, all Bernoulli trials with success probability p, then their sum is distributed according to a binomial distribution with parameters n and p:

  ${\displaystyle \sum _{k=1}^{n}X_{k}\sim \operatorname {B} (n,p)}$ (binomial distribution).^[3]

The Bernoulli distribution is simply ${\displaystyle \operatorname {B} (1,p)}$, also written as ${\textstyle \mathrm {Bernoulli} (p).}$

• The categorical distribution is the generalization of the Bernoulli distribution for variables with any constant number of discrete values.
• The Beta distribution is the conjugate prior of the Bernoulli distribution.^[5]
• The geometric distribution models the number of independent and identical Bernoulli trials needed to get one success.
• If ${\textstyle Y\sim \mathrm {Bernoulli} \left({\frac {1}{2}}\right)}$, then ${\textstyle 2Y-1}$ has a Rademacher distribution.

• Bernoulli process, a random process consisting of a sequence of independent Bernoulli trials
• Bernoulli sampling
• Binary entropy function
• Binary decision diagram

• Johnson, N. L.; Kotz, S.; Kemp, A. (1993). Univariate Discrete Distributions (2nd ed.). Wiley. ISBN 0-471-54897-9.
• Peatman, John G. (1963). Introduction to Applied Statistics. New York: Harper & Row. pp. 162–171.

Wikimedia Commons has media related to Bernoulli distribution.

• "Binomial distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994].
• Weisstein, Eric W. "Bernoulli Distribution". MathWorld.
• Interactive graphic: Univariate Distribution Relationships.