1729 (number)
| ||||||||||||||||||||||||||||||||
Read other articles:

Erythrina Erythrina corallodendron Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Plantae Divisi: Magnoliophyta Kelas: Magnoliopsida Subkelas: Rosidae Ordo: Fabales Famili: Fabaceae Subfamili: Faboideae Tribus: Phaseoleae Genus: ErythrinaL., 1753 Spesies tipe Erythrina corallodendronL.[1] Spesies Lihat teks Sinonim[2][3] Chirocalyx Meisn. (1843) Corallodendron Mill. (1754) Duchassaingia Walp. (1850) Erythina (lapsus) Hypaphorus Hassk. (1858) Macrocymbium Walp. (1853) ...

Albrecht AltdorferNama dalam bahasa asli(de) Albrecht Altdorfer BiografiKelahiran1480 Regensburg Kematian12 Februari 1538 (Kalender Masehi Gregorius) (57/58 tahun)Regensburg Data pribadiAgamaGereja Lutheran KegiatanSpesialisasiSeni lukis dan arsitektur PekerjaanPelukis, arsitek, illuminator (en), pembuat grafis, engraver (en) dan master builder (en) AliranRenaisans Jerman Karya kreatifKarya terkenal(1510 dekade) Legend of Saint Florian (en)(1520 dekade) Nativity of the Virgin (en)(1526) Susan...

Canadian ice hockey player Ice hockey player Jeremy Welsh Born (1988-04-30) April 30, 1988 (age 35)Bayfield, Ontario, CanadaHeight 6 ft 3 in (191 cm)Weight 210 lb (95 kg; 15 st 0 lb)Position CentreShoots LeftErste Liga teamFormer teams HSC CsíkszeredaCarolina HurricanesVancouver CanucksSt. Louis BluesFischtown PinguinsDüsseldorfer EGHC Dynamo PardubiceGrizzlys WolfsburgKrefeld PinguineCracoviaNottingham PanthersNHL Draft UndraftedPlaying career 2012&#...

Robin TunneyRobin Tunney (2013)PekerjaanAktrisTahun aktif1992 ─ sekarangSuami/istriBob Gosse (1997–2006) (cerai)Andrew Dominik (2007–sekarang) Robin Tunney (lahir 19 Juni 1972) merupakan seorang aktris berkebangsaan Amerika Serikat. Dia dilahirkan di Chicago, orangtuanya keturunan Irlandia. Dia berkarier di dunia film sejak 1992. Dia dikenal karena perannya sebagai Teresa Lisbon di serial televisi The Mentalist (2008–2015) dan perannya sebagai Veronica Donovan di Prison Break (2...

Domestic airport in Kanpur, Uttar Pradesh, India Kanpur AirportIATA: KNUICAO: VECXSummaryAirport typePublic/MilitaryOwnerAirports Authority of IndiaOperatorAirports Authority of IndiaServesKanpurLocationChakeri, Kanpur, Uttar Pradesh, IndiaElevation AMSL410 ft / 126 mCoordinates26°23′58″N 80°25′37″E / 26.3994624°N 80.4269499°E / 26.3994624; 80.4269499MapKNU/VECXShow map of Uttar PradeshKNU/VECXShow map of IndiaRunways Direction Length Surface...

Football tournament season 2012–13 Svenska CupenTournament detailsCountrySwedenDates3 June 2012 – 26 May 2013Teams103 (including qualifying)96 (competition proper)Final positionsChampionsIFK Göteborg (6th title)Runner-upDjurgårdens IFTournament statisticsMatches played119Goals scored403 (3.39 per match)Top goal scorer(s)Tobias Hysén (8 goals)[1]← 20112013–14 → The 2012–13 Svenska Cupen was the 57th season of Svenska Cupen and the first s...

金正男遇刺现场,位于吉隆坡第二国际机场 金正男遇刺事件,是2017年2月13日已故朝鮮勞動黨總書記金正日的長子,也是現任領導人金正恩的兄長金正男於吉隆坡第二国际机场被2名女子刺殺身亡的事件。 事件经过 2017年2月6日,一名持姓名为「金哲」的朝鲜民主主义人民共和国外交护照的男子搭機抵达马来西亚,在2月8日前往浮羅交怡並在浮羅交怡威斯汀酒店(The Westin Langkaw...

Norwegian ice hockey player Ice hockey player Ken André Olimb Ken André Olimb, 2023Born (1989-01-21) January 21, 1989 (age 35)Oslo, NorwayHeight 5 ft 10 in (178 cm)Weight 179 lb (81 kg; 12 st 11 lb)Position Left wingShoots LeftDEL teamFormer teams Schwenninger Wild WingsVålerenga IshockeyFrisk Asker IshockeyDüsseldorfer EGLinköpings HCNational team NorwayPlaying career 2006–present Ken André Olimb (born January 21, 1989) is a Norwegian...

Politically-charged firing Letter from President Donald Trump dismissing FBI Director James Comey Trump–Russia relations Business interactions Bayrock Group Business projects of Donald Trump in Russia Trump Tower Moscow Russian election interference 2016 US election leaks Associates' links with Russian officials and spies Cambridge Analytica Classified information disclosures Clinton emails Cyberwarfare by Russia Data seizure DCLeaks Democratic National Committee cyber attacks Democratic Na...

Governor of Oklahoma since 2019 Kevin StittStitt in 202228th Governor of OklahomaIncumbentAssumed office January 14, 2019LieutenantMatt PinnellPreceded byMary Fallin Personal detailsBornJohn Kevin Stitt (1972-12-28) December 28, 1972 (age 51)Milton, Florida, U.S.NationalityAmericanCherokee NationPolitical partyRepublicanSpouse Sarah Hazen (m. 1998)[1]Children6Residence(s)Edmond, Oklahoma, U.S.EducationOklahoma State University–Stillwater (BS) ...
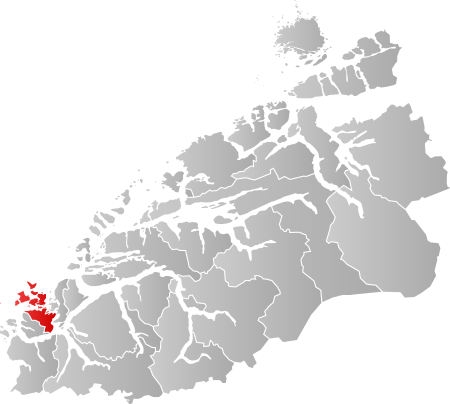
Lambang Lokasi Untuk kotamadya di Nordland silakan lihat Heroey i Nordland Kota utama Fosnavåg Bergsøy, pulau utama Pulau Runde Herøy ialah sebuah kotamadya di provinsi Møre og Romsdal, Norwegia. Pusatnya ada di Fosnavag, terletak di pulau Bergsoy. Herøy terdiri atas 8 pulau, antara lain Runde, terkenal karena koloni burung lautnya yang besar dan Skorpa, terkenal atas perannya sebagai stasiun bus Shetland. Herøyfjord membagi 2 kotamadya Herøy. Sebuah stasiun perikanan, Flåvær terleta...

Dieser Artikel befasst sich mit dem Staat Kuwait. Zur Hauptstadt Kuwaits siehe Kuwait (Stadt). Staat Kuwait arabisch دولة الكويت Daulat al-Kuwait Flagge Wappen Amtssprache Arabisch Hauptstadt Kuwait Staats- und Regierungsform Konstitutionelle Monarchie Staatsoberhaupt EmirMischal al-Ahmad al-Dschabir as-Sabah Regierungschef PremierministerScheich Ahmad al-Abdullah as-Sabah Fläche 17.818 km² Einwohnerzahl 4,3 Millionen (126.) (2020; Schätzung)[1] Bevölkerungsdichte 2...

École biblique et archéologique française de Jérusalem UbicazioneStato Israele CittàGerusalemme Dati generaliFondazione1890 FondatoreMarie-Joseph Lagrange TipoIstituto di esegesi e archeologia biblica RettoreOlivier Poquillon, O.P. (direttore) Mappa di localizzazione Sito web Modifica dati su Wikidata · Manuale L'École biblique et archéologique française de Jérusalem (EBAF) è un'istituzione francese di insegnamento superiore e di ricerca, fondata e diretta dall'Ordine dei...

Para otros usos, véase Tuna (desambiguación). Una tuna es una agrupación o hermandad de estudiantes universitarios o miembros de una sociedad que, portando la vestimenta antigua de la universidad o vestimenta que represente su cultura de origen, se caracterizan por cantar, tocar y viajar por el mundo gracias a estas habilidades —a pesar de que no todos o muy pocos sean músicos de profesión— o por interpretar temas musicales haciendo uso generalmente de instrumentos de cuerda y percu...

Cet article est une ébauche concernant le jeu vidéo et l’univers Pokémon. Vous pouvez partager vos connaissances en l’améliorant (comment ?) (voir l’aide à la rédaction). Pokémon ÉcarlatePokémon VioletLogos francophones des deux jeux.Développeur Game FreakÉditeur NintendoThe Pokémon CompanyDistributeur NintendoRéalisateur Shigeru OhmoriScénariste Ryota MuranakaCompositeur Go Ichinose (Compositeur principal)Toby Fox[1]Minako AdachiJunichi MasudaHiromitsu MaebaTeruo Ta...

Language family For other uses, see Caspian languages. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Northeast Caucasian languages – news · newspapers · books · scholar · JSTOR (September 2008) (Learn how and when to remove this message) Northeast CaucasianEast CaucasianNakh-DaghestanianNorth CaspianCaspia...

Brazilian Parnassian poet, journalist and translator This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Olavo Bilac – news · newspapers · books · scholar · JSTOR (May 2015) (Learn how and when to remove this message) Olavo BilacBilac, c. 1895BornOlavo Brás Martins dos Guimarães Bilac(1865-12-16)16 December 18...

South Sudanese Australian comedian This biographical article is written like a résumé. Please help improve it by revising it to be neutral and encyclopedic. (September 2024) Emo MajokEmo in 2023Birth nameEmmanuel Gureec MajokBorn (1988-08-06) 6 August 1988 (age 36)EthiopiaMediumStand-upNationalitySouth Sudanese AustralianYears active2018–presentGenresObservational comedypolitical satiresurreal humorblack comedySubject(s)Social liferefugeespoliticseconomical lifereligionrelat...

Random search tree data structure TreapTypeRandomized binary search treeTime complexity in big O notationOperation Average Worst caseSearch O(log n) O(n)Insert O(log n) O(n)Delete O(log n) O(n)Space complexitySpace O(n) O(n) Part of a series onProbabilisticdata structures Bloom filter Count sketch Count–min sketch Quotient filter Skip list Random trees Random binary tree Treap Rapidly exploring random tree Related Randomized algorithm HyperLogLog vte In computer science, the treap and the r...

Air terjun Yōrō di musim gugur Air Terjun Yōrō (養老の滝code: ja is deprecated , Yōrō no Taki) adalah objek wisata air terjun yang ada di Taman Yōrō yang terletak di kota Yōrō, Distrik Yōrō, Gifu, Jepang. Keadaan alam Air terjun ini memiliki ketinggian 32 meter dan lebar 4 meter. Air dari air terjun ini dipuji atas kualitas airnya yang tinggi. Air Terjun Yōrō dan Kikusuisen termasuk ke dalam daftar Seratus Air Terjun Terbaik di Jepang dan Seratus Mata Air Terbaik di Jepang. ...










