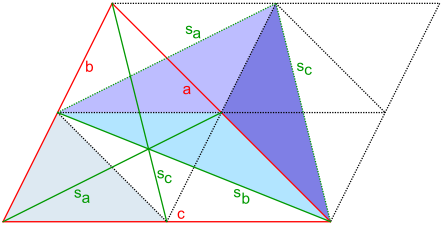
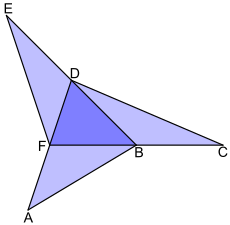
Seitenhalbierende
|
Read other articles:
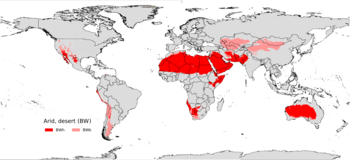
Wilayah dengan iklim gurun BWh (iklim gurun panas) BWk (iklim gurun dingin) Iklim gurun adalah iklim di mana ada kelebihan penguapan di atas presipitasi. Permukaan yang biasanya botak, berbatu, atau berpasir di iklim gurun menyimpan sedikit kelembaban dan menguapkan sedikit curah hujan yang mereka terima. Meliputi 14,2% dari luas daratan bumi, gurun panas adalah jenis iklim paling umum di bumi[1] setelah iklim kutub. Meskipun tidak ada bagian dari Bumi yang dik...

I'm YoursSingel oleh Jason Mrazdari album We Sing. We Dance. We Steal Things.Dirilis15 April 2008FormatDigital download, CD singleDirekam2005GenrePop, reggae, folk rockDurasi4:03LabelAtlanticPenciptaJason MrazProduserMartin Terefe I'm Yours adalah singel pertama dari Jason Mraz dari album studio ketiganya We Sing. We Dance. We Steal Things.. Singel ini dirilis pada tanggal 15 April 2008. Sertifikasi Negara Sertifikasi(sales thresholds) Jerman Gold[1] Spanyol Gold[2] AS 5x Plat...

Historic house in Nevada, United States Nevada State Historic Preservation Office PDF documents United States historic placeLakeview HouseU.S. National Register of Historic Places 2012 photoShow map of NevadaShow map of the United StatesLocationU.S. 395 south of E. Lake Blvd., Carson City, NevadaCoordinates39°12′29″N 119°48′13″W / 39.20806°N 119.80361°W / 39.20806; -119.80361Area3.1 acres (1.3 ha)Built1873Built byVirginia City & Gold Hill Water Co....

Park in Atlanta, Georgia For the park in Olympia, Washington, see Woodruff Park (Olympia). Wide sidewalk along the park's east side Playground spelling ATL in Woodruff Park International Peace Fountain on the park's northern edge Woodruff Park, named for Robert W. Woodruff, is located in the heart of Downtown Atlanta, Georgia. The park's 6 acres (2.4 ha)[1] are north of Edgewood Ave, between Peachtree Street NE and Park Place NE. The park includes a fountain, a performance pavili...

Commercial offices in Atlanta, Georgia101 Marietta StreetFormer namesCentennial TowerGeneral informationTypeCommercial officesArchitectural styleModernismLocation101 Marietta Street NWAtlanta, GeorgiaCoordinates33°45′24″N 84°23′31″W / 33.7568°N 84.3919°W / 33.7568; -84.3919Completed1975OwnerThe Dilweg CompaniesHeightRoof140 m (460 ft)Technical detailsFloor count36Floor area674,994 sq ft (62,709.0 m2)Design and constructionArchitect...

American college basketball season 1969–70 Illinois Fighting Illini men's basketballConferenceBig Ten ConferenceRecord15–9 (8–6 Big Ten)Head coachHarv SchmidtAssistant coaches Dick Campbell Jim Wright MVPMike PriceCaptains Mike Price Randy Crews Home arenaAssembly HallSeasons← 1968–691970–71 → 1969–70 Big Ten Conference men's basketball standings vte Conf Overall Team W L PCT W L PCT No. 7 Iowa 14 – 0 1.000 2...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vishwakarma Institute of Technology – news · newspapers · books · scholar · JSTOR (March 2015) (Learn how a...

Tetikus dan alas tetikus Alas tetikus atau tatakan tetikus (Inggris: mousepad) adalah sebuah permukaan untuk menempatkan dan menggerakan tetikus komputer. Alas tetikus menunjang pemakaian tetikus secara langsung di atas sebuah meja dengan menyediakan sebuah permukaan yang membolehkannya untuk mengukur gerak secara akurat dan tanpa hambatan. Riwayat Pada sebuah presentasi tahun 1968 dari Douglas Engelbart yang menandai debut publik dari tetikus,[1] Engelbart memakai konsol kontrol ...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1]...

Pakistani mufti (1936–2022) Grand Mufti[1]Muhammad Rafi Usmaniمحمد رفیع عثمانی3rd President of Darul Uloom KarachiIn office1986 – 18 November 2022Preceded byAbdul Hai ArifiSucceeded byTaqi UsmaniVice-president of Wifaq-ul-MadarisIn office5 October 2017 – 16 June 2021 PersonalBorn(1936-07-21)21 July 1936Deoband, United Provinces, British IndiaDied18 November 2022(2022-11-18) (aged 86)Karachi, Sindh, PakistanResting placeDarul Uloom Karachi cem...

Piazza Brembanacomune Piazza Brembana – VedutaPanorama LocalizzazioneStato Italia Regione Lombardia Provincia Bergamo AmministrazioneSindacoStefano Ambrosioni (lista civica Piazza in Valle) dal 27-5-2019 TerritorioCoordinate45°56′50″N 9°40′30″E / 45.947222°N 9.675°E45.947222; 9.675 (Piazza Brembana)Coordinate: 45°56′50″N 9°40′30″E / 45.947222°N 9.675°E45.947222; 9.675 (Piazza Brembana) Altitudine518 ...

This article is about the historical region of Dasharna. For the kingdom in Indian Epic Literature, see Dasarna Kingdom. Dasharna (Sanskrit:दशार्ण Daśārṇa) was an ancient Indian janapada (realm) in eastern Malwa region between the Dhasan River and the Betwa River. The name of the janapada was derived from the Daśārṇa, the ancient name of the Dhasan River.[1] The janapada was also known as Akara[2] and Rudradaman I in his Junagarh rock inscription referred t...

Sekolah Tinggi Agama Buddha Negeri Raden WijayaKetuaProf. Dr. Hesti Sadtyadi, S.E., M.Si.LokasiWonogiri, Jawa Tengah, IndonesiaAlamatJl. Kantil Bulusulur Wonogiri 57651, Bulusari, Bulusulur, Wonogiri, Wonogiri, Jawa TengahAfiliasiKementerian Agama Republik IndonesiaSitus webradenwijaya.ac.id Sekolah Tinggi Agama Buddha Negeri Raden Wijaya (STABN Raden Wijaya) adalah salah satu perguruan tinggi negeri yang berada di Wonogiri, Jawa Tengah. STABN Raden Wijaya merupakan perguruan tinggi di lingku...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Class of UK elections A map showing the wards of Westminster from 2002 to 2022 Westminster City Council, the local authority of the City of Westminster in London, England, is elected every four years. Since the last boundary changes in 2022 the council has comprised 54 councillors representing 18 wards, with each ward electing three councillors. Elections are held every four years.[1] Results summary From the first elections to the council in 1964 until 2022, overall political control...

Taoist meditative text ZuowanglunTraditional Chinese坐忘論Simplified Chinese坐忘论Literal meaningsitting forgetting discussionTranscriptionsStandard MandarinHanyu PinyinZuòwànglùnWade–GilesTso-wang lun Image of Sima Chengchen. The Zuowanglun or Zuowang lun is a Taoist meditative text that was written by the Shangqing School patriarch Sima Chengzhen (647–735). Taoism incorporated many Buddhist practices during the Tang dynasty (618–907), and the Zuowanglun combined med...

Coppa dell'AFC 20132013 AFC Cup Competizione Coppa dell'AFC Sport Calcio Edizione 10ª Organizzatore AFC Date dal 5 marzoal 2 novembre 2013 Partecipanti 33 Nazioni 18 Risultati Vincitore Kuwait SC(3º titolo) Secondo Al-Qadisiya Statistiche Miglior giocatore Bader Al-Mutawa Miglior marcatore Issam Jemâa (16) Incontri disputati 118 Gol segnati 409 (3,47 per incontro) Pubblico 504 544 (4 276 per incontro) Cronologia della competizione 2012 2014 Man...

Begonia teuscheri Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Rosid Ordo: Cucurbitales Famili: Begoniaceae Genus: Begonia Spesies: Begonia teuscheri Nama binomial Begonia teuscheriLinden ex André Begonia teuscheri adalah spesies tumbuhan yang tergolong ke dalam famili Begoniaceae. Spesies ini juga merupakan bagian dari ordo Cucurbitales. Spesies Begonia teuscheri sendiri merupakan bagian dari genus ...

Governing body of the Russian Orthodox Church For the Holy Synod of the Moscow Patriarchate between 1721 and 1917, see Most Holy Synod. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Holy Synod of the Russian Orthodox Church – news · newspapers · books · scholar · JSTOR (October 2012) (Learn how and when to...