Ecke
|
Read other articles:

JejungwonPoster promosiGenreDrama medis Drama sejarahDitulis olehLee Ki-wonSutradaraHong Chang-wookPemeranPark Yong-wooHan Hye-jinYeon Jung-hoonNegara asalKorea SelatanBahasa asliKoreaJmlh. episode36 (Korea Selatan)ProduksiLokasi produksiKoreaDurasiSenin dan Selasa pukul 21:55 (WSK)Rumah produksiKim Jong-hak ProductionRilis asliJaringanSBSRilis4 Januari (2010-01-04) –4 Mei 2010 (2010-5-4) Jejungwon (Hangul: 제중원; Hanja: 濟眾院) adalah drama medi...

Symphonic black metalDimmu Borgir tampil di tahun 2005Sumber aliran Symphonic metal black metal Sumber kebudayaanAwal hingga pertengahan 1990-an, Norwegia dan Inggris Raya Symphonic black metal adalah subgenre dari black metal yang muncul pada 1990-an dan menggabungkan elemen simfoni dan orkestra.[1] Band simfoni black metal terkenal termasuk Dimmu Borgir, Emperor, Carach Angren dan Demonic Resurrection. Sejarah Band metal ekstrim pertama yang memasukkan elemen orkestra ke dalam musik...

Artikel ini bukan mengenai Malaka, kabupaten di Indonesia. Untuk kegunaan lain, lihat Malaka (disambiguasi). Melaka dan George Town, Kota Bersejarah Selat MalakaSitus Warisan Dunia UNESCOKriteriaBudaya: ii, iii, ivNomor identifikasi1223Pengukuhan2008 (ke-32) Balai Kota Melaka Kota Melaka atau Kota Malaka (Bahasa Melayu: Bandar Melaka), atau juga dikenal dengan julukan Melaka Bandaraya Bersejarah, adalah ibu kota negara bagian Melaka di Malaysia. Melaka yang berupa hasil reklamasi dapat d...

Very high velocity This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hypervelocity – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this template message) The energy flash of a hypervelocity impact during a laboratory simulation of what happens when a piece of orbital...

Former railway station in England This article is about a closed station latterly named Lord's but previously named St. John's Wood. For the current station of that name, see St John's Wood tube station. Lord'sLord'sLocation of Lord's in Central LondonLocationSt John's WoodOwnerMetropolitan RailwayNumber of platforms2Key dates13 April 1868 (1868-04-13)Opened as St. John's Wood Road1 April 1925Rebuilt; renamed St. John's Wood11 June 1939Renamed Lord's20 November 1939&#...

Small wild cat Flat-headed cat Conservation status Endangered (IUCN 3.1)[2] CITES Appendix I (CITES)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Carnivora Suborder: Feliformia Family: Felidae Subfamily: Felinae Genus: Prionailurus Species: P. planiceps[1] Binomial name Prionailurus planiceps[1](Vigors & Horsfield, 1827) Distribution of the flat-headed cat, 2015[2] The flat-...

Early-to-mid-1980s music cultural movement This article is about the Second British Invasion. For the 1960s British music movement, see British Invasion. Second British InvasionPart of the 1980s in the United States and United KingdomDuration1982–mid-1980sLocationUnited States, United KingdomCauseRise of British synth-pop and new wave artists in U.S. pop music charts The Second British Invasion was a sharp increase in the popularity of British synth-pop and new wave artists in the United S...

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1]...
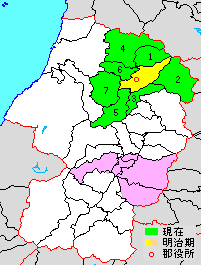
Lokasi munisipalitas yang ada di Distrik Mogami, Prefektur Yamagata1. – Kaneyama 2. – Mogami3. – Funagata4. – Mamurogawa5. – Ōkura6. – Sakegawa7. – Tozawawarna hijau - cakupan wilayah distrik saat iniwarna kuning - bekas wilayah distrik pada awal zaman Meijiwarna pink - cakupan wilayah distrik pada zaman pra-Meiji Distrik Mogami (最上郡code: ja is deprecated , Mogami-gun) adalah sebuah distrik yang terletak di Prefektur Yamagata, Jepang. Per 1 Oktober 2020, distrik ini memil...

UlpianusPatung Ulpianus dari abad ke-19 di Palais de Justice di kota Brussels, Belgia.LahirSekitar tahun 170Meninggal223RomaKebangsaanRomawiPekerjaanAhli hukum Ulpianus (bahasa Latin: Gnaeus Domitius Annius Ulpianus; sekitar tahun 170 – 223) adalah seorang ahli hukum Romawi keturunan Tirus. Ia dianggap sebagai salah satu ahli hukum terbaik pada masanya. Ia juga merupakan salah satu dari lima ahli hukum yang dijadikan sebagai otoritas hukum menurut lex citationum yang dikel...

Circondario del Reno-Lahncircondario(DE) Rhein-Lahn-Kreis LocalizzazioneStato Germania Land Renania-Palatinato DistrettoNon presente AmministrazioneCapoluogoBad Ems TerritorioCoordinatedel capoluogo50°16′N 7°52′E / 50.266667°N 7.866667°E50.266667; 7.866667 (Circondario del Reno-Lahn)Coordinate: 50°16′N 7°52′E / 50.266667°N 7.866667°E50.266667; 7.866667 (Circondario del Reno-Lahn) Altitudine275 m s.l.m. Superficie782,31 k...

Dario CostaDario Costa press conference Challenger Cup Lake Balaton 2019Born9 May 1980 (1980-05-09) (age 43)Manchester, United KingdomNationalityItalianWebsitedariocosta.com Dario Costa (born 9 May 1980, Manchester, United Kingdom) born to an Iranian mother and an Italian father, is an Italian professional Red Bull Air Race competitor, stunt pilot, aerobatic performer, flight instructor, Pilatus PC6 Porter paradropping pilot and author from Bologna, Italy[1] and is the firs...

1985 American film Wizards of the Lost KingdomTheatrical release posterDirected byHéctor OliveraWritten byEd Naha (as Tom Edwards)Produced by Frank Isaac Alex Sessa Starring Bo Svenson Vidal Peterson Thom Christopher Barbara Stock María Socas CinematographyLeonardo Rodríguez SolísEdited bySilvia RipollMusic by Christopher Young James Horner (from Battle Beyond the Stars) Distributed byConcorde PicturesRelease date May 17, 1985 (May 17, 1985) CountriesUnited StatesArgentinaLanguageEng...

Untuk jenis makanan, lihat otak-otak. Untuk otak manusia dan otak hewan, lihat otak. Lingkungan Akihabara di Tokyo, sebuah lokasi berkumpul yang populer bagi otaku Bagian dari seri tentangAnime dan manga Anime Sejarah Industri Animasi net orisinal Animasi video orisinal Fansub Fandub Perusahaan Seri terpanjang Daftar Manga Sejarah Pasar internasional Mangaka Dōjinshi Scanlation Alternatif Gekiga Yonkoma Penerbit Seri terlaris Seri terpanjang Daftar Kelompok demografi Anak-anak Dewasa Shōnen...

Chan di Prancis Terbuka 2015 Chan Hao-ching Hanzi tradisional: 詹皓晴 Hanzi sederhana: 詹皓晴 Alih aksara Mandarin - Hanyu Pinyin: Zhān Hàoqíng Chan Hao-ching (lahir 19 September 1993), yang juga disebut Angel Chan, adalah seorang pemain tenis profesional yang mewakili Tiongkok Taipei. Ia biasanya menjadi spesialis ganda, memenangkan 8 WTA dan 8 ITF dalam disiplin tersebut. Di Kejuaraan Wimbledon 2014, Chan meraih babak akhir ganda campuran dengan Max Mirnyi untuk meraih final grand ...

French archaeologist and Egyptologist (1821–1881) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Auguste Mariette – news · newspapers · books · scholar · JSTOR (January 2016) (Learn how and when to remove this message) Auguste MarietteAuguste Mariette. Photo by Nadar, c. 1861BornFrançois Auguste Fe...

Halaman ini berisi artikel tentang seorang stand up comedian atau komika. Untuk penyanyi, lihat Tulus (penyanyi). Gideon TulusLahirGideon Victor Tulus Parulian23 Agustus 1999 (umur 24)Cibinong, Jawa Barat, IndonesiaNama lainGideon TulusAlmamaterPoliteknik Negeri JakartaPekerjaanPelawak tunggalAktorTahun aktif2016—sekarang Gideon Victor Tulus Parulian (lahir 23 Agustus 1999) adalah seorang pelawak tunggal dan aktor berkebangsaan Indonesia. Tulus, begitu ia kerap disapa, adalah...

South Korean singer and actor (born 1982) In this Korean name, the family name is Song. Song Won-geunBorn (1982-12-17) December 17, 1982 (age 41)Seoul, South KoreaOther namesRUNOccupation(s)Singer, actorYears active2000–presentAgentJ & EnterpriseKorean nameHangul송원근Hanja宋元根Revised RomanizationSong Won-geunMcCune–ReischauerSong Wŏn-kŭn Song Won-geun (Korean: 송원근; born December 17, 1982) is a South Korean singer and actor. Song made his entert...

بنك جمهورية غينيا المركزي البلد غينيا المقر كوناكري تاريخ إنشاء 1960 المحافظ كاراموا كابا[1] العملة فرنك غيني الموقع الالكتروني الموقع الرسمي تعديل مصدري - تعديل بنك جمهورية غينيا المركزي هو البنك المركزي في غينيا. يقع البنك في العاصمة كوناكري.[2]...

Ancient Roman bridge, a landmark of Rome, Italy Pons CestiusItalian: Ponte CestioThe Pons Cestius in its modern form The Roman bridge around 1880, before its reconstructionCoordinates41°53′24.8″N 12°28′38″E / 41.890222°N 12.47722°E / 41.890222; 12.47722Carriespedestrians, motor vehiclesCrossesTiberTiber Island–Trastevere(Piazza S. Bartolomeo all'Isola–Lungotevere degli Anguillara)LocaleRome, ItalyNext upstreamPonte GaribaldiNext downstreamPonte Palatino...




