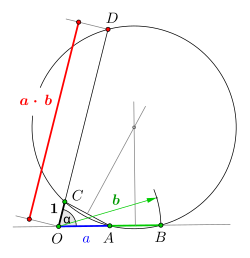
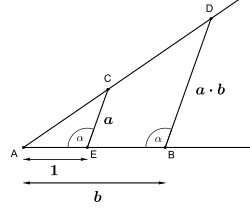
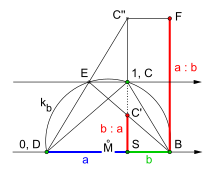
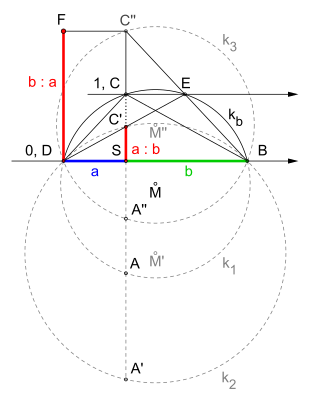
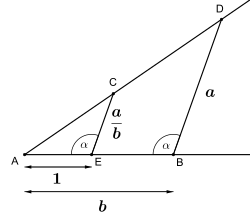
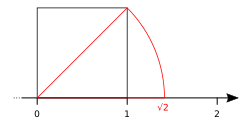
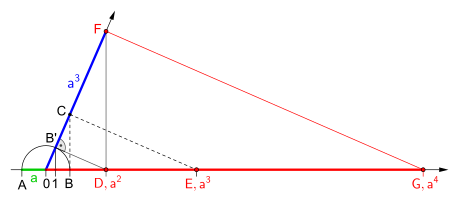
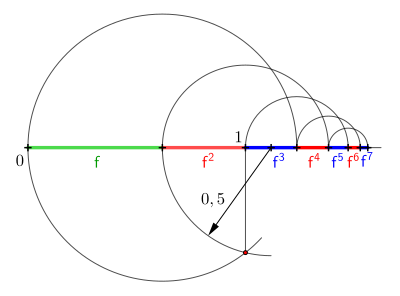
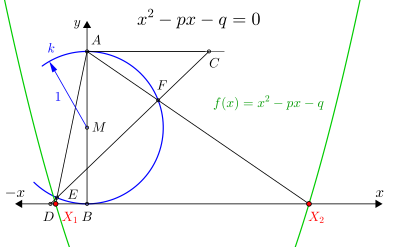
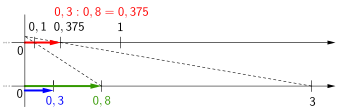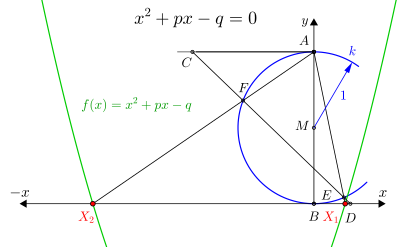Konstruktion mit Zirkel und Lineal
|
Read other articles:

Adi ShankaracharyaPatung Adi Shankara di sebuah kuil di Mysore.LahirShankara788 M[1]Kaladi, Kerajaan Cherakini Kerala, IndiaMeninggal820 M[1]Kedarnath, Kerajaan Palakini Uttarakhand, India Adi Shankara (dilafalkan [aːd̪i ɕəŋkəɾə]; awal abad ke-8[2][note 1])—disebut pula (Adi) Shankaracharya dan Shankara Bhagavatpada, dapat dieja Sankaracharya, (Ādi) Śaṅkarācārya, Ādi Śaṅkarācāri,[5] Śaṅkara Bhagavatpāda, Śaṅkara Bhagavatpā...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Eko Londo – berita · surat kabar · buku · cendekiawan · JSTOR Eko LondoLahirOng Lie Oen(1957-08-01)1 Agustus 1957Surabaya, Jawa TimurMeninggal24 November 2023(2023-11-24) (umur 66)Surabaya, Jawa Tim...

Seorang Gigant Dalam mitologi Yunani, Gigant (bahasa Yunani: Γίγαντες) adalah raksasa yang merupakan anak Gaia (bumi). Gaia melahirkan para Gigant setelah dibuahi oleh darah Uranus. Dalam mitologi Setelah Zeus dan sudara-saudaranya mengalahkan para Titan dalam perang Titanomakhia, mereka mengambil alih kekuasaan atas dunia dan mengurung para Titan di Tartarus. Hal ini membuat Gaia marah sehingga Gaia menyuruh para Gigant untuk melawan para dewa Olimpus. Para Gigant pun berperang m...

Eimi Naruse Eimi Naruse (成瀨瑛美code: ja is deprecated , Naruse Eimi, lahir di Kooriyama, Fukushima, Jepang pada 16 Februari)[1] adalah seorang penyanyi, pemeran dan idola asal Jepang. Ia menjadi anggota grup idola Dempagumi.inc pada 3 Juni 2010. Ia adalah mantan anggota unit Mizutama Online (水玉おんらいん) dengan Furukawa Mirin. Ia adalah produsen merek busana BABYUUN. Referensi ^ でんぱ組 魔法の質問に妄想を爆発. デイリースポーツ. 神戸新聞社...

Moto2KategoriBalap motorNegara atau daerahInternasionalMusim pertama2010Tim15PabrikanMV Agusta, Kalex, BoscoscuroPemasok banDunlopJuara rider Remy GardnerJuara konstruktor KalexSitus webMotoGP.com Musim saat ini Kejuaraan Dunia Moto2 (atau biasa disebut Moto2 saja atau nama resminya FIM Moto2 World Championship) merupakan sebuah seri atau kelas dari Grand Prix Sepeda Motor. Kelas Moto2 mulai diperlombakan di musim 2010 dengan adanya perubahan regulasi untuk kelas 250cc. Kelas ini merupakan ke...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Dalam hukum kanon Gereja Katolik, kehilangan jabatan rohaniwan (umumnya disebut sebagai laikisasi) adalah pencabutan uskup, imam atau deakon dari status seorang anggota rohaniwan. Dalam Gereja Katolik, uskup, imam atau deakon yang dilepaskan dari jaba...

Gastón Silva 2017, olahraga, sepak bola, pertandingan internasional persahabatan OEFB - Austria vs Uruguay.Informasi pribadiNama lengkap Gastón SilvaTanggal lahir 5 Maret 1994 (umur 30)Tempat lahir Salto, UruguayTinggi 185 cm (6 ft 1 in)Posisi bermain BekInformasi klubKlub saat ini IndependienteNomor 20Karier senior*Tahun Tim Tampil (Gol)2017 – Independiente 12 (1)Tim nasional2014 – Uruguay 17 (0) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik...

NY-12 redirects here. The term may also refer to New York State Route 12. U.S. House district for New York New York's 12th congressional districtInteractive map of district boundaries since January 3, 2023Representative Jerry NadlerD–New YorkDistribution100% urban0% ruralPopulation (2022)705,008[1]Median householdincome$142,104[2]Ethnicity65.2% White14.1% Asian11.2% Hispanic4.7% Black3.9% Two or more races0.9% otherCook PVID+34[3] New York's 12th congressional ...

У этого термина существуют и другие значения, см. Женщина-кошка (значения) и Кайл. Не следует путать с Чёрной кошкой — персонажем Marvel Comics. Женщина-кошкаангл. Catwoman Женщина-кошка (Селина Кайл) на обложке комикса Catwoman (vol. 3) #59Художник — Адам Хьюз[англ.] История публикаций �...

Nama ini menggunakan cara penamaan Portugis. Nama keluarga pertama atau maternalnya adalah Mota Veiga dan nama keluarga kedua atau paternalnya adalah de Carvalho Silva. Bernardo Silva Silva bersama Portugal pada Piala Dunia FIFA 2018Informasi pribadiNama lengkap Bernardo Mota Veiga de Carvalho e Silva[1]Tanggal lahir 10 Agustus 1994 (umur 29)Tempat lahir Lisboa, PortugalTinggi 1,73 m (5 ft 8 in)Posisi bermain Gelandang, PenyerangInformasi klubKlub saat ini Manc...

Portrait de Louis XIV en costume de sacre, 1701, par Hyacinthe Rigaud. Cathédrale Notre-Dame de Reims. Du temps du royaume des Francs puis de France, l'avènement du nouveau roi était légitimé par la cérémonie de son couronnement avec la couronne de Charlemagne à Notre-Dame de Reims. Cependant, le roi n'avait pas besoin d'être reconnu comme monarque français ; le nouveau roi montait sur le trône automatiquement à la mort de son prédécesseur, cela étant symbolisé une p...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Artikel ini sudah memiliki referensi, tetapi tidak disertai kutipan yang cukup. Anda dapat membantu mengembangkan artikel ini dengan menambahkan lebih banyak kutipan pada teks artikel. (Maret 2019) (Pelajari cara dan kapan saatnya untuk menghapus pesa...

Judging another culture solely by the values and standards of one's own culture Polish sociologist Ludwig Gumplowicz is believed to have coined the term ethnocentrism in the 19th century, although he may have merely popularized it. Ethnocentrism in social science and anthropology—as well as in colloquial English discourse—means to apply one's own culture or ethnicity as a frame of reference to judge other cultures, practices, behaviors, beliefs, and people, instead of using the standards ...

State park in Ashe County, North Carolina New River State ParkIUCN category III (natural monument or feature)Location of New River State Park in North CarolinaShow map of North CarolinaNew River State Park (the United States)Show map of the United StatesLocationAshe, North Carolina, United StatesCoordinates36°24′55″N 81°23′14″W / 36.41528°N 81.38722°W / 36.41528; -81.38722[1]Area3,323 acres (13.45 km2)[2]Elevation2,716 ft (828 ...

Livre de DurrowDébut de l'évangile de Marc, f.86rDate fin du VIIe siècleTechnique enluminures sur parcheminDimensions (H × L) 24,5 × 14,5 cmFormat 248 folios reliésNo d’inventaire Ms.57Localisation Bibliothèque de Trinity College, Dublin ( Irlande)modifier - modifier le code - modifier Wikidata Le Livre de Durrow (Book of Durrow en anglais) est un évangéliaire manuscrit enluminé de la fin du VIIe siècle typique de l'art hiberno-saxon. Il a l...

Decreto RattazziIl ministro dell'interno Urbano RattazziTitolo estesoLegge 23 ottobre 1859, n. 3702 Tipo leggeLegge ordinaria LegislaturaVI ProponenteUrbano Rattazzi SchieramentoSinistra storica Promulgazione23 ottobre 1859 A firma diVittorio Emanuele II La legge 23 ottobre 1859 n. 3702 (nota anche come decreto Rattazzi o legge Rattazzi) fu una legge del Regno di Sardegna, emanata su iniziativa del ministro dell'interno del regno, Urbano Rattazzi[1], per ridisegnare la geografia ammin...

Russian military commander (1729/30–1800) Suvorov redirects here. For other uses, see Suvorov (disambiguation) and Alexander Suvorov (disambiguation). In this name that follows Eastern Slavic naming customs, the patronymic is Vasilyevich and the family name is Suvorov. Generalissimo, PrinceAlexander SuvorovRymnikskyAlexander Suvorov by Charles de Steuben (1815)Native nameАлександр Васильевич СуворовOther name(s)Aleksandr Vasilevich Suvorov[1]Nickname(s)...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يوليو 2019) منتخب ألمانيا لكرة القاعدة تعديل مصدري - تعديل منتخب ألمانيا الوطني لكرة ال...

British television presenter Not to be confused with Ranveer Singh. Ranvir SinghSingh in 2010Born (1977-08-11) 11 August 1977 (age 46)[1]Preston, Lancashire, EnglandAlma materLancaster University, University of Central LancashireOccupationsJournalisttelevision presenterYears active2002 – presentEmployerITVNotable credits BBC North West Tonight (2005–2012) Daybreak (2012–2014) Lorraine (2020–present) Good Morning Britain (2014–present) ITV News (2014–2020) St...

Computer error message This article is about the error message. For the EP by White Town, see >Abort, Retry, Fail?_. MS-DOS prompts Abort, Retry, Fail? after being commanded to list a directory with no diskette in the drive using the dir command. Abort, Retry, Fail? (or Abort, Retry, Ignore?) is an error message found in DOS operating systems, which prompts the end-user for a course of action to follow. Although an improvement over CP/M,[1] the message has been cited as an example ...





![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)