Kanadischer Wacholder

Kanadischer Wacholder

Kanadischer Wacholder (Juniperus communis var. depressa)

Systematik
Familie: Zypressengewächse (Cupressaceae)
Unterfamilie: Cupressoideae
Gattung: Wacholder (Juniperus)
Sektion: Juniperus
Art: Gemeiner Wacholder (Juniperus communis)
Varietät: Kanadischer Wacholder
Wissenschaftlicher Name
Juniperus communis var. depressa
Pursh

Der Kanadische Wacholder (Juniperus communis var. depressa) ist eine Varietät des Gemeinen Wacholders (Junipuers communis) aus der Familie der Zypressengewächse (Cupressaceae). Sie ist in weiten Teilen Nordamerikas heimisch.

Beschreibung

Zweig mit Nadeln und Beerenzapfen

Der Kanadische Wacholder wächst meist als immergrüner, mehrstämmiger, niederliegender Strauch, seltener auch als kleiner Baum. Die Strauchform erreicht Wuchshöhen von bis zu 3 Metern, die Bäume werden bis zu 6, in Ausnahmefällen auch bis zu 10 Meter hoch. Die faserige Borke blättert in dünnen Streifen ab und ist anfangs braun, verfärbt sich mit der Zeit aber grau. Die Äste gehen gerade oder aufsteigend vom Stamm ab.[1]

Die nadelförmigen Blätter werden 0,8 bis 1,5 Zentimeter lang und haben eine spitz zulaufende oder zugespitzte Spitze. Sie weisen blaugrüne Stomatabänder auf.[1]

Der Kanadische Wacholder ist zweihäusig (diözisch). Die weiblichen Beerenzapfen werden 0,6 bis 0,9 Zentimeter dick. Jeder der Zapfen trägt drei Samenkörner.[1]

Die Chromosomenzahl beträgt 2n = 22.[2]

Verbreitung und Standort

Das natürliche Verbreitungsgebiet des Kanadischen Wacholders liegt in Kanada und weiten Teilen der USA. In Kanada findet man die Art in allen Provinzen und Territorien. In den USA erreicht das Verbreitungsgebiet in Alaska den nördlichsten und in Kalifornien, Arizona und New Mexico den südlichsten Punkt. Weiters erstreckt es sich von der West- bis zur Ostküste. Fossile Überreste der Art, welche aus der in Nordamerika als Wisconsin glaciation bekannten Kaltzeit stammen, wurden in den südlichen Appalachen gefunden.[1]

Der Kanadische Wacholder gedeiht in Höhenlagen von 0 bis 2800 Metern. Er wächst dort auf felsigen Böden an Hängen und auf Berggipfeln.[1]

Systematik

Die Erstbeschreibung als Juniperus communis var. depressa erfolgte 1814 durch Frederick Traugott Pursh in Flora Americae Septentrionalis; or, a Systematic Arrangement and Description of the Plants of North America, Band 2, Seiten 646–647. Synonyme für Juniperus communis var. depressa Pursh sind Juniperus communis subsp. depressa (Pursh) Franco und Juniperus depressa (Pursh) Raf.[3]

Quellen

  • Christopher J. Earle: Juniperus communis var. depressa. In: The Gymnosperm Database. www.conifers.org, 23. November 2012, abgerufen am 24. März 2013 (englisch).
  • Frank D. Watson, James E. Eckenwalder: Cupressaceae. Juniperus. In: Flora of North America Editorial Committee (Hrsg.): Flora of North America North of Mexico. Pteridophytes and Gymnosperms. Volume 2. Oxford University Press, New York u. a. 1993, ISBN 0-19-508242-7, Juniperus communis var. depressa (englisch, Juniperus communis var. depressa – Online – dieses Werk ist textgleich Online).

Einzelnachweise

  1. ↑ a b c d e Christopher J. Earle: Juniperus communis var. depressa. In: The Gymnosperm Database. www.conifers.org, 23. November 2012, abgerufen am 24. März 2013 (englisch).
  2. ↑ Frank D. Watson, James E. Eckenwalder: Cupressaceae. Juniperus. In: Flora of North America Editorial Committee (Hrsg.): Flora of North America North of Mexico. Pteridophytes and Gymnosperms. Volume 2. Oxford University Press, New York u. a. 1993, ISBN 0-19-508242-7, Juniperus communis var. depressa (englisch, Juniperus communis var. depressa – Online – dieses Werk ist textgleich Online).
  3. ↑ Juniperus communis var. depressa bei Tropicos.org. Missouri Botanical Garden, St. Louis, abgerufen am 24. März 2013.
Commons: Kanadischer Wacholder – Sammlung von Bildern, Videos und Audiodateien

Read other articles:

Euler–Bernoulli beam theory

Method for load calculation in construction This vibrating glass beam may be modeled as a cantilever beam with acceleration, variable linear density, variable section modulus, some kind of dissipation, springy end loading, and possibly a point mass at the free end. Euler–Bernoulli beam theory (also known as engineer's beam theory or classical beam theory)[1] is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection ...

 

رونكونكوما (نيويورك)

رونكونكوما     الإحداثيات 40°48′50″N 73°07′42″W / 40.8139°N 73.1283°W / 40.8139; -73.1283  [1] تقسيم إداري  البلد الولايات المتحدة[2][3]  التقسيم الأعلى آيسلب  خصائص جغرافية  المساحة 21.10399 كيلومتر مربع21.147016 كيلومتر مربع (1 أبريل 2010)[4]  ارتفاع 34 متر ...

 

Haroun Tazieff

Vous lisez un « bon article » labellisé en 2022. Pour les articles homonymes, voir Tazieff. Haroun TazieffHaroun Tazieff, président du premier Festival international de géographie en 1990.FonctionsConseiller régional de Rhône-Alpes1992-1995Conseiller municipal de Grenoble1989-1995Conseiller général de l'Isère1988-1994Secrétaire d'ÉtatGouvernement Laurent Fabius1983-1986BiographieNaissance 11 mai 1914Varsovie (Empire russe)Décès 2 février 1998 (à 83 ans)4e arron...

Jane Hadley Barkley

Jane Hadley Barkley Istri Wakil Presiden Amerika SerikatMasa jabatan18 November 1949 – 20 Januari 1953PendahuluBess TrumanPenggantiPat Nixon Informasi pribadiLahir(1911-09-23)23 September 1911Keytesville, Missouri, Amerika SerikatMeninggal6 September 1964(1964-09-06) (umur 52)Washington, D.C., Amerika SerikatPartai politikDemokratSuami/istriAlben BarkleySunting kotak info • L • B Elizabeth Jane Rucker Hadley Barkley (23 September 1911 – 6 Septembe...

 

House of Orléans

French noble family, a cadet branch of the House of Bourbon House of OrléansBourbon-OrléansCapetian royal familyArms of the House of OrléansParent houseBourbonCountryFranceBrazil[Note 1]Founded10 May 1661; 362 years ago (1661-05-10)FounderPhilippe I, Duke of OrléansCurrent headJean d'Orléans, Count of ParisHeads of cadet branches:Alfonso de Orléans-Borbón, Duke of GallieraBertrand of Orléans-BraganzaPedro of Orléans-Braganza and PetrópolisFinal rulerLouis P...

 

Confessions Part II

2004 single by Usher Confessions Part IISingle by Usherfrom the album Confessions ReleasedJune 1, 2004RecordedJuly 2003GenreR&BLength3:49LabelAristaSongwriter(s)Usher RaymondJermaine DupriBryan-Michael CoxProducer(s)Jermaine DupriBryan-Michael CoxUsher singles chronology Burn (2004) Confessions Part II (2004) My Boo (2004) Music videoConfessions Part II on YouTubeAudioConfessions Part II on YouTubeConfessions Part II Remix on YouTube Confessions Part II is a song by R&B singer Usher, ...

National Shrine of Our Lady of Fatima

Roman Catholic church in Valenzuela, Philippines This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: National Shrine of Our Lady of Fatima – news · newspapers · books · scholar · JSTOR (February 2024) (Learn how and when to remove this message) Church in Valenzuela, PhilippinesNational Shrine of Our Lady of Fati...

 

Quarter-wave impedance transformer

Using a transmission line as an impedance transformer. A quarter-wave impedance transformer, often written as λ/4 impedance transformer, is a transmission line or waveguide used in electrical engineering of length one-quarter wavelength (λ), terminated with some known impedance. It presents at its input the dual of the impedance with which it is terminated. The relationship between the characteristic impedance, Z0, input impedance, Zin and load impedance, ZL is: Z i n Z 0 = Z 0 Z L {\displa...

 

Méthode de Chapman-Enskog

À la fin du XIXe siècle on connaît l'équation de Boltzmann qui régit la dynamique du milieu gazeux à l'échelle microscopique et les équations d'Euler et de Navier-Stokes pour le niveau macroscopique. Le passage d'une échelle à l'autre constitue une partie du sixième problème de Hilbert. David Hilbert, auteur des énoncés des problèmes jugés majeurs à la fin du XIXe siècle pose les bases d'une méthode sous forme d'un développement qui porte son nom (1912). Il faudr...

Grain (textile)

Orientation of the threads A close-up image of the grain of blue woven chambray fabric For woven textiles, grain refers to the orientation of the weft and warp threads. The three named grains are straight grain, cross grain, and the bias grain. In sewing, a pattern piece can be cut from fabric in any orientation, and the chosen grain or orientation will affect the way the fabric hangs and stretches and thus the fit of a garment. Generally speaking a piece is said to be cut on a particular gra...

 

قوة

  لمعانٍ أخرى، طالع قوة (توضيح). قوةيمكن وصف القوى بأنها دفع أو سحب للأجسام، ويمكن للقوى أن تنشأ نتيجة لظواهر مثل الجاذبية أو المغناطيسية أو أي ظاهرة أخرى تؤدي إلى تغيير في تعجيل الجسم.معلومات عامةالرموز الشائعة F → {\displaystyle {\vec {F}}} , F, Fالتعريف الرياضي F = d p d t {\displaystyle {\b...

 

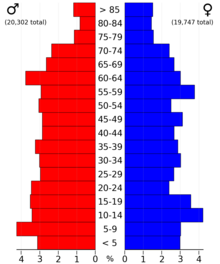
Marshall County, Iowa

County in Iowa, United States County in IowaMarshall CountyCountyThe courthouse in Marshalltown is on the NRHPLocation within the U.S. state of IowaIowa's location within the U.S.Coordinates: 42°02′03″N 93°00′04″W / 42.034166666667°N 93.001111111111°W / 42.034166666667; -93.001111111111Country United StatesState IowaFounded1846Named forJohn MarshallSeatMarshalltownLargest cityMarshalltownArea • Total573 sq mi (1,480 km2)...

Husainid dynasty

Cretan Turkish ruling dynasty of Tunis For other uses, see Husaynids. Husainid dynastyCountryBeylik of Tunis Kingdom of TunisiaFounded15 July 1705FounderHussein ICurrent headMuhammad XI HabibFinal rulerMuhammad VIII al-AminTitlesBey, King of TunisiaDeposition25 July 1957 The Husainid dynasty or Husaynid dynasty (Arabic: الحسينيون) was a ruling Turkish dynasty of the Beylik of Tunis. The dynasty was of Greek origin from the island of Crete.[1][2][3][4]&...

 

Повесть о посаднике Щиле

Повесть о посаднике Щиле Посадник Щил приготовляет для себя гроб и саван («Повесть о посаднике Щиле», лицевая рукопись, ок. 1838 г.) Жанр повесть Язык оригинала древнерусский Дата написания XV век — XVI век Текст произведения в Викитеке Медиафайлы на Викискладе По́весть ...

 

Daniel Ricciardo

Daniel RicciardoDaniel Ricciardo nel 2022Nazionalità Australia Altezza180 cm Automobilismo CategoriaFormula 1 RuoloPilota Squadra RB CarrieraCarriera in Formula 1Esordio10 luglio 2011 Stagioni2011- Scuderie HRT 2011 Toro Rosso 2012-2013 Red Bull 2014-2018 Renault 2019-2020 McLaren 2021-2022 AlphaTauri 2023 RB 2024- Miglior risultato finale3º (2014, 2016) GP disputati249 (248 partenze) GP vinti8 Podi32 Punti ottenuti1 326 Pole position3 Giri ...

Customer equity

Total combined customer lifetime values of all of the company's customers This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Customer equity – news · newspapers · books&#...

 

Château de Montfort

For the castle with the same name in Côte-d'Or, see Château de Montfort (Cote-d'Or). For the castle with the same name in Yvelines, see Montfort-l'Amaury. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Château de Montfort – news · newspapers · books · scholar · JSTOR (July 2015) (Learn how and when to re...

 

Dongguan railway station (Guangdong)

Railway station in Dongguan, Guangdong, China This article is about the current Dongguan railway station. For the railway station which named Dongguan before 2014, see Changping railway station (Guangdong). Dongguan东莞General informationLocationBetween Chashan and Shilong, Dongguan, GuangdongChinaCoordinates23°05′29″N 113°51′17″E / 23.09139°N 113.85472°E / 23.09139; 113.85472Operated byGuangshen Railway Company (a subsidiary of the Guangzhou Railway Grou...

Vicarius

Latin word meaning substitute or deputy For other uses of vicar, see Vicar (disambiguation). Politics of ancient Rome Periods Roman Kingdom753–509 BC Roman Republic509–27 BC Roman Empire27 BC – AD 395 Principate27 BC – AD 284 DominateAD 284–641 WesternAD 395–476 EasternAD 395–1453 Timeline Constitution Kingdom Republic Sullan republic Empire Augustan reforms Late Empire Political institutions Imperium Collegiality Auctoritas Roman citizenship Cursus honorum Assemblies Centuriate...

 

Darryl David

David pada 2021 David Darryl Wilson (bahasa Tamil: டேரல் டேவிட் Ṭēral Tēviṭ; kelahiran 1970),[1] yang lebih dikenal sebagai Darryl David, adalah seorang politikus dan mantan penyiar media Singapura. Sebagai anggota Partai Aksi Rakyat, ia menjadi anggota Parlemen ke-14 sejak 2015.[2][3] David juga menjadi kepala jabatan eksekutif SJI International School.[4] Referensi ^ Kesalahan pengutipan: Tag <ref> tidak sah; tidak ditemu...