Geordneter Körper
|
Read other articles:

Madjid Bougherra Bougherra pada tahun 2012Informasi pribadiNama lengkap Madjid BougherraTanggal lahir 7 Oktober 1982 (umur 41)Tempat lahir Longvic, PrancisTinggi 1,90 m (6 ft 3 in)Posisi bermain BekInformasi klubKlub saat ini Tanpa klubKarier junior1999–2000 AS Quetigny2000–2002 AS LongvicKarier senior*Tahun Tim Tampil (Gol)2002–2006 Gueugnon 49 (1)2006 → Crewe Alexandra (pinjaman) 11 (1)2006–2007 Sheffield Wednesday 28 (2)2007–2008 Charlton Athletic 34 (2)200...

Gulfstream G100, sebelumnya dikenal sebagai Astra SPX, adalah jet bisnis-bermesin ganda diproduksi Israel Aircraft Industries, sekarang diproduksi untuk Gulfstream Aerospace . Sebutan Angkatan Udara Amerika Serikat untuk G100 adalah C-38 Courier. Referensi Artikel bertopik pesawat terbang dan penerbangan ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

MagojaSeorang pria Korea mengenakan magojaJenismantelBahankainTempat asalKorea Magoja (마고자) adalah jenis mantel luar tradisional Korea, baik untuk pria maupun wanita.[1] Sejarah Tidak seperti baji (celana), jeogori (baju atas) dan chima (rok) dan durumagi (jubah) yang mempunyai sejarah yang panjang, magoja adalah varian dari magua (bahasa Korea: 마과, magwa), jenis pakaian yang diperkenalkan dari Dinasti Qing.[1] Magoja dipopulerkan ke Korea setelah Heungseon Daewongun...

Al-Qur'an Sejarah Wahyu Kesejarahan Asbabunnuzul Nuzululqur'an Manuskrip Samarkand Sanaa Birmingham Topkapi Pembagian Hizb Juz Manzil Muqatta'at Surah Daftar Makiyah Madaniyah Isi Eskatologi Hewan Keajaiban Ketuhanan Ilmu pengetahuan Legenda Nabi dan Rasul Nama lain Perumpamaan Wanita Membaca Taawuz Basmalah Hafiz Qiraat Qari Tajwid Tartil Khatam Terjemahan Daftar terjemahan Al-Qur'an Tafsir Daftar karya tafsir Hermeneutika Takwil Nasakh Hubungan dengan kitab lain Orang yang disebut namanya K...

قرية باريش الإحداثيات 43°24′20″N 76°07′34″W / 43.4056°N 76.1261°W / 43.4056; -76.1261 [1] تقسيم إداري البلد الولايات المتحدة[2] خصائص جغرافية المساحة 4.15738 كيلومتر مربع4.157412 كيلومتر مربع (1 أبريل 2010) ارتفاع 151 متر عدد السكان عدد السكان 447 (1 أبريل 2020)[...

العلاقات الأسترالية الكولومبية أستراليا كولومبيا أستراليا كولومبيا تعديل مصدري - تعديل العلاقات الأسترالية الكولومبية هي العلاقات الثنائية التي تجمع بين أستراليا وكولومبيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدو�...

PangebatanDesaHalaman depan Balai desaNegara IndonesiaProvinsiJawa TengahKabupatenBanyumasKecamatanKaranglewasKode pos53161Kode Kemendagri33.02.18.2002 Luas185,92 haJumlah penduduk6316Kepadatan- Pangebatan adalah desa di kecamatan Karanglewas, Banyumas, Jawa Tengah, Indonesia. Geografis Desa Pangebatan terletak di Barat Daya Kota Purwokerto, Ibu kota Kabupaten Banyumas dekat dengan 3 aliran sungai yaitu Sungai Banjaran, Sungai Jengok dan Sungai Logawa. Batas wilayah Batas-batas desa Pang...

Japanese manga magazine Big Comic SuperiorCover of February 22, 2008, issueCategoriesSeinen manga[1][2]FrequencySemimonthly on 2nd and 4th FridaysCirculation108,667[2](July–September, 2016)First issueJuly 1, 1987[3]CompanyShogakukanCountryJapanBased inTokyoLanguageJapaneseWebsitebigcomicbros.net/bigsuperior/ Big Comic Superior (ビッグコミックスペリオール, Biggu Komikku Superiōru) is a semimonthly seinen manga magazine published since July 1, 198...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Kerajaan Polandia 1025–1385 – berita · surat kabar · buku · cendekiawan · JSTOR Kerajaan PolandiaKrólestwo Polskie (pl)Regnum Poloniae (la)1025–1385 Bendera kerajaan Lambang Rentang terluas Ker...

Argentine association football player This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (August 2021) Nicolás Tagliafico Tagliafico with Argentina at the 2018 FIFA World CupPersonal informationFull name Nicolás Alejandro Tagliafico[1]Date of birth (1992-08-31) 31 August 1992 (age 31)[1]Place of birth Rafael Calzada, Buenos Aire...

Para otros usos de este término, véase Europa (desambiguación). Europa Gentilicio: europeo, -a Superficie 10 530 751 km²Población 741 651 840 (2024 est.)[1] hab.Densidad 71 hab./km²Subdivisiones Europa del NorteEuropa del SurEuropa del EsteEuropa del OesteEuropa CentralPaíses 50 Albania Alemania Andorra Austria Bélgica Bielorrusia Bosnia y Herzegovina Bulgaria Ciudad del Vaticano Croacia Din...

Seseorang yang mengacungkan jari tengah Dalam budaya Barat, mengacungkan jari tengah (juga disebut fuck[1] atau flipping someone off dalam bahasa Inggris)[1] adalah sebuah gestur tak senonoh. Isyarat ini menyampaikan pesan menghina dalam tingkat menengah hingga ekstrem, dan kurang lebih sepadan dengan ungkapan fuck me, fuck you, shove it up your ass/arse, up yours atau go fuck yourself. Gestur ini dibuat dengan menunjukkan bagian belakang telapak tangan dengan jari tengah yang...

Голубянки Самец голубянки икар Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ПервичноротыеБез ранга:ЛиняющиеБез ранга:PanarthropodaТип:ЧленистоногиеПодтип:ТрахейнодышащиеНадкласс:ШестиногиеКласс...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Jeanne HarvilliersJan Lücken - gravure du XVIIe siècle - un bûcher en 1544.BiographieNaissance 1528VerberieDécès 30 avril 1578RibemontActivité SorcièreFamille Sa mère morte sur le bûcher à Senlis en 1548.Autres informationsCondamnée pour Sorcellerie (1578)Condamnation Peine de mortmodifier - modifier le code - modifier Wikidata Jeanne Harvilliers, dite la sorcière de Ribemont ou la sorcière de Verberie, née à Verberie, en 1528[1] et morte sur le bûcher à Ribemont, le 30 ...

Someone who is rejected or cast out, as from home or societyNot to be confused with Outcaste.For other uses, see Outcast (disambiguation). Look up outcast or pariah in Wiktionary, the free dictionary. An outcast is someone who is rejected or cast out, as from home or from society[1] or in some way excluded, looked down upon, or ignored. In common English speech, an outcast may be anyone who does not fit in with normal society, which can contribute to a sense of isolation. Compar...

This article is about the EA Sports video game series. For the original Super Nintendo NCAA Basketball Game, see NCAA Basketball (video game). Video game seriesGenre(s)Sports (basketball)Developer(s)Electronic Arts, EA CanadaPublisher(s)EA SportsPlatform(s)PlayStation, PlayStation 2, Xbox, Xbox 360, PlayStation 3First releaseNCAA March Madness 98February 25, 1998Latest releaseNCAA Basketball 10November 17, 2009 NCAA Basketball (formerly NCAA March Madness) is a series of college basketball vi...
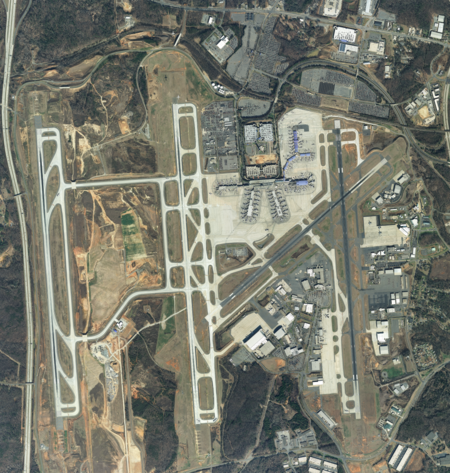
Airport serving Charlotte, North Carolina, United States Charlotte Douglas International AirportAn aerial view of Charlotte Douglas International Airport in 2012IATA: CLTICAO: KCLTFAA LID: CLTWMO: 72314SummaryAirport typePublicOwner/OperatorCity of CharlotteServesCharlotte metropolitan areaLocation5501 Josh Birmingham ParkwayCharlotte, North Carolina, U.S.Opened1935; 89 years ago (1935)Hub forAmerican AirlinesElevation AMSL748 ft / 228 mCoordinates35°12′50�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. OlginateseLogo USD Olginatese CalcioNama lengkapUnione Sportiva Dilettantistica OlginateseBerdiri1968StadionStadio Comunale,Olginate, Italy(Kapasitas: 1,050)KetuaFlavio RedaelliManajerAlessio DelpianoLigaSerie D/B2011–12Serie D/B, 3rd Kostum kandang ...

25°21′22″N 49°37′25″E / 25.356002°N 49.6236547°E / 25.356002; 49.6236547 حي المحدود حي الملك فهد الإحداثيات 25°21′22″N 49°37′25″E / 25.356002°N 49.6236547°E / 25.356002; 49.6236547 تقسيم إداري قائمة الدول السعودية منطقة المنطقة الشرقية محافظة الأحساء حي الملك فهد حي المحدود خصائص �...




























































