Ordnungstopologie
|
Read other articles:

Italian politician (1896–1956) For other people named Renato Ricci, see Renato Ricci (disambiguation). You can help expand this article with text translated from the corresponding article in Italian. (April 2020) Click [show] for important translation instructions. View a machine-translated version of the Italian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the...

Incipit of a letter Quattuor abhinc annos (Latin for four years ago) is the incipit of a letter that the Congregation for Divine Worship and the Discipline of the Sacraments sent on 3 October 1984 to presidents of episcopal conferences concerning celebration of Mass in the Tridentine form. History The letter explained that previously Pope John Paul II had invited comments from the bishops concerning the reception of the Missal promulgated in 1970 by authority of Pope Paul VI in accordance wit...

Egon VIIICount of Fürstenberg-HeiligenbergCoat of arms of FürstenbergPredecessorFrederick IV of FürstenbergSuccessorHerman Egon, Prince of FürstenbergBornErnst Egon of Fürstenberg-Heiligenberg1588Died1635Noble familyFürstenbergSpouse(s)Anna Maria of Hohenzollern-HechingenIssuesee belowFatherLandgrave Frederick IV of FürstenbergMotherCountess Elisabeth of Sulz Egon VIII of Fürstenberg-Heiligenberg (Ernst Egon; 21 March 1588 in Speyer – 24 August 1635 in Constance) was Imperial Count ...

Halaman ini berisi artikel tentang tokoh-tokoh sejarah. Untuk kompetisi sepak bola Amerika Selatan, lihat Copa Libertadores. Konferensi Guayaquil (1822) antara Simón Bolívar dan José de San Martín, libertadores (pembebas) terbesar Spanyol Amerika. Libertadores (bahasa Spanyol: [liβertaˈðoɾes], bahasa Portugis: [libeʁtaˈdoɾis]) yang berarti Pembebas, mengacu pada para pemimpin utama dari perang kemerdekaan Amerika Latin atas penjajahan Spanyol dan Portugal. Pemberian juluk...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2024. Kolese Katolik SangjiJenisSwasta, KatolikDidirikan1970PresidenYu Gang-haLokasiAndong, Gyeongsang Utara, Korea Selatan36°34′10″N 128°44′10″E / 36.56944°N 128.73599°E / 36.56944; 128.73599Koordinat: 36°34′10″N...

General purpose helicopter This Bell UH-1Y is equipped with a FLIR and rocket pods, demonstrating its versatility as a utility helicopter A utility helicopter is a multi-purpose helicopter capable of pursuing a wide array of tasks. They have proven useful in both civilian as well as military operations, with versatility being their defining trait. Civil Helicopters play a crucial role in various aspects of civilian safety. Police and fire rescue aircraft demonstrate exceptional versatility ac...

ناصر إبراهيمي معلومات شخصية الميلاد 20 أغسطس 1940 (84 سنة) طهران الجنسية إيران مسيرة الشباب سنوات فريق 1962–1965 شاهين طهران المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1965–1968 شاهين طهران 1968–1970 استقلال طهران 1970–1979 برق شيراز الفرق التي دربها 1980–1984 إيران (مساعد) 1984–1985 إيرا...

Our Lady of Mount Carmel of New York The Madonna of East HarlemThe canonically crowned image out in public processionLocationEast Harlem, New York City, New York, United StatesDate1884WitnessAntonio PetrucciApprovalPope Leo XIIIPope Pius XShrineOur Lady of Mount Carmel Parish Building in New York, United StatesChurch of Our Lady of Mount CarmelThe facade of the churchGeneral informationTown or cityNew York, New YorkCountryUnited StatesConstruction started1884ClientRoman Catholic Archdiocese ...

College basketball team Chicago Maroons men's basketballUniversityUniversity of ChicagoHead coachMike McGrath (17th season)ConferenceUniversity Athletic Association (UAA)ArenaRatner Athletics Center (Capacity: 1,658)NicknameMaroonsColorsMaroon and white[1] Pre-tournament Premo-Porretta champions1909Pre-tournament Helms champions1907, 1908, 1909NCAA tournament appearancesDivision III: 1997, 1998, 2000, 2001, 2007, 2008Conference regular season championsBig Te...

Моли́тва в иудаи́зме — под словом «молитва» в талмудическом иудаизме обычно подразумевают как общинную молитву, так и личную мольбу[1]. Различают молитвы Торы (Храма) и Талмуда (синагог). Молитва может быть разнообразной[2][3][4]: תפלה (тфила — «моли...

Italian footballer (born 1987) Giuseppe Rossi Rossi with Villarreal CFPersonal informationFull name Giuseppe Rossi[1]Date of birth (1987-02-01) 1 February 1987 (age 37)[2]Place of birth Teaneck, New Jersey, United StatesHeight 1.73 m (5 ft 8 in)[3]Position(s) ForwardYouth career1996–1999 Clifton Stallions2000–2004 Parma2004 Manchester UnitedSenior career*Years Team Apps (Gls)2004–2007 Manchester United 5 (1)2006 → Newcastle United (loan) 11 ...

Азиатский барсук Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКласс:Мле�...

Hobbyist or actor attempts to recreate battles or events from the American Civil War Confederate reenactors fire their rifles during a reenactment of the Battle of Chancellorsville in May 2008. Confederate artillery reenactors fire on U.S. soldier reenactors during a Battle of Chickamauga reenactment in Danville, Illinois. American Civil War reenactment is an effort to recreate the appearance of a particular battle or other event associated with the American Civil War by hobbyists known (in t...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 2007 Tampa mayoral election – news · newspapers · books · scholar · JSTOR (October 2019) Tampa mayoral election, 2007← 20032011 → Candidate Pam Iorio Marion Serious Lewis Aria Ray Green Party Nonpartisan Nonpartisan Nonpa...

Second World War fleet of the Royal Navy British Pacific FleetFive of the six fleet aircraft carriers of the British Pacific Fleet c. 1945Active1944–45Country United KingdomBranchRoyal Navyalso:Royal Australian NavyRoyal Canadian NavyRoyal New Zealand NavyTypeFleetEngagements Operation Meridian Battle of Okinawa Naval bombardments of Japan CommandersNotablecommandersBruce FraserMilitary unit The British Pacific Fleet (BPF) was a Royal Navy formation that saw action against Japan during...
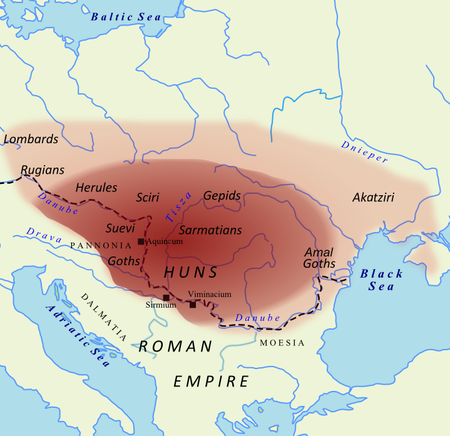
Ancient Germanic people in Eastern Europe For the Iraqi political party formerly known as SCIRI, see Islamic Supreme Council of Iraq. Effigy of Odoacer, who is thought to be of Scirian descent The Sciri, or Scirians, were a Germanic people. They are believed to have spoken an East Germanic language. Their name probably means the pure ones. The Sciri were mentioned already in the late 3rd century BC as participants in a raid on the city of Olbia near modern-day Odesa. In the late 4th century t...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) مسجد ت...

لمعانٍ أخرى، طالع إنا (توضيح). هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يناير 2019) إنا (باليابانية: 伊奈町) إنا (اليابان) خريطة الموقع تاريخ التأسيس 1 نوفمبر 1970 تقسيم إداري البلد اليابان ...

العلاقات السلوفينية المالية سلوفينيا مالي سلوفينيا مالي تعديل مصدري - تعديل العلاقات السلوفينية المالية هي العلاقات الثنائية التي تجمع بين سلوفينيا ومالي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة س�...









![{\displaystyle \{x\in X\,\mid \,a<x<b\}=:\left]a,b\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05103df2f709ed6f0860f169da283432b65d9932)


![{\displaystyle \{x\in X\,\mid \,a\leq x\leq b\}\;=:\;\left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48b05447530ee2f2d8c35136d900e08aabff7cad)
![{\displaystyle \left[a,b\right]\;\;=\;\;X\,\setminus \,{\bigl (}\left]-\infty ,b\right[\,\cup \,\left]a,\infty \right[{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c2da06e7b748b9d76f55cab556e7efe5733634b)





















![{\displaystyle \left]a,+\infty \right[:=\{x\in X\,\mid \,a<x\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cba45abac27548880b2e1d38f862aa2dd65005a1)

![{\displaystyle \left]-\infty ,b\right[:=\{x\in X\,\mid \,x<b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb88ba3f042aed2bc1bd6183442e5ae9d6746411)









![{\displaystyle =\left]a,b\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba0b94916fa97437de015e5fd95a6cbbbbb196a0)

![{\displaystyle =\left]a,\infty \right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c218fe82d230382376a632124de6fb53eeef3dc)

![{\displaystyle =\left]-\infty ,b\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f69ea2c0865ebec3361880ac22e43a54fbbb52b2)
![{\displaystyle =\left]-\infty ,\infty \right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5397121fd8a7ae4a44f719d6d5a66902c3b993f)
![{\displaystyle \{x\in X\,\mid \,x<b\}=\;\textstyle \bigcup _{a<b}\left]a,b\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/287b88f4cdcd5790242af841cfdd190b15e3ef70)