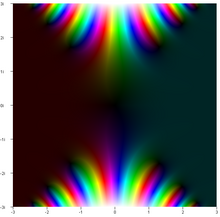
Fehlerfunktion
|
Read other articles:

Wharton India Economic ForumAbbreviationWIEFFormation1996TypeBusiness ConferencePurposeTo raise the profile of the economic potential of IndiaLocationPhiladelphia, Pennsylvania, United StatesChairpersonsDeeksha Senguttuvan, Kanupriya Raman, Kumar Sambhava , Pranav Damani, Shreeya BhutaniWebsitewww.whartonindiaeconomicforum.com The Wharton India Economic Forum (WIEF), established in 1996 at The Wharton School, is a student-run business forum in the United States focused on India.[1] WI...

1941 film by Josef von Sternberg The Shanghai GestureTheatrical release posterDirected byJosef von SternbergScreenplay byJosef von SternbergGeza HerczegJules FurthmanBased onthe play The Shanghai Gestureby John ColtonProduced byArnold PressburgerStarringGene TierneyWalter HustonVictor MatureOna MunsonCinematographyPaul IvanoEdited bySam WinstonMusic byRichard HagemanProductioncompanyArnold Pressburger FilmsDistributed byUnited ArtistsRelease date December 25, 1941 (1941-12-25)&...

قرية لانكاستر الإحداثيات 42°54′02″N 78°40′12″W / 42.9006893°N 78.6701142°W / 42.9006893; -78.6701142 [1] تاريخ التأسيس 1849 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة إيري خصائص جغرافية المساحة 7.1 كيلومتر مربع ارتفاع 205 متر عدد الس...

Pour les articles homonymes, voir Adenot. Sophie AdenotSophie Adenot lors de son intégration au corps d'astronautes de l'ESA, le 23 novembre 2022 à Paris.BiographieNaissance 5 juillet 1982 (41 ans)Cosne-Cours-sur-LoireNom de naissance Sophie Marie Laurence AdenotNationalité françaiseFormation Maison d'éducation de la Légion d'honneur de Saint-Denis (d) (jusqu'en 1999)Institut supérieur de l'aéronautique et de l'espace (2001-2003)Massachusetts Institute of Technology (2004)École...

Cet article est une ébauche concernant la politique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Dans un système parlementaire, l'opposition désigne le ou les groupes parlementaires qui ne soutiennent pas le gouvernement. Dans certains pays, l'opposition parlementaire jouit d'un statut propre, notamment dans les pays utilisant le système de Westminster. Dans ces derniers, le parti d'opposition le plus im...

سافاليا تقسيم إداري البلد اليونان [1] خصائص جغرافية إحداثيات 37°49′12″N 21°17′43″E / 37.819981°N 21.295298°E / 37.819981; 21.295298 المساحة 13.05 كيلومتر مربع الارتفاع 15 متر السكان التعداد السكاني 1196 (resident population of Greece) (2001)1128 (resident population of Greece) (1991)1101 (resident population of Greece) (2021)12...

Region of Gangwon Province, North Korea This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Yeongseo – news · newspapers · books · scholar · JSTOR (April 2018) YeongseoHangul영서Hanja嶺西Revised RomanizationYeongseoMcCune–ReischauerYŏngsŏNorth Korean nameHangul령서Hanja嶺西Revised Romanizat...

Strada statale 82della Valle del LiriLocalizzazioneStato Italia Regioni Abruzzo Lazio Province L'Aquila Frosinone Latina DatiClassificazioneStrada statale InizioSS 5 presso Avezzano FineSS 7 presso Itri Lunghezza126,800 km Data apertura1928 Provvedimento di istituzioneLegge 17/05/1928 n°1094[1] GestoreANAS (tratta Avezzano-Arce) e Astral (tratta Ceprano-Itri) dal 2007 Percorso Manuale La strada statale 82 della Valle del Liri (SS 82), ora anche strada re...

This article is about the commune in Paris. For the Nazi concentration camp, see Fort de Romainville. Commune in Île-de-France, FranceRomainvilleCommuneThe church of Saint-Germain-l'Auxerrois, designed by Alexandre-Théodore Brongniart Coat of armsParis and inner ring departmentsLocation of Romainville RomainvilleShow map of FranceRomainvilleShow map of Île-de-France (region)Coordinates: 48°53′02″N 2°26′06″E / 48.884°N 2.435°E / 48.884; 2.435CountryFrance...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

American politician (born 1950) For the Australian comedian, see Gerry Connolly (comedian). Gerry ConnollyOfficial portrait, 2022Member of the U.S. House of Representativesfrom Virginia's 11th districtIncumbentAssumed office January 3, 2009Preceded byTom DavisPresident of the NATO Parliamentary AssemblyIn officeNovember 23, 2020 – November 28, 2022Preceded byAttila MesterházySucceeded byJoëlle Garriaud-MaylamChair of the Fairfax County Board of SupervisorsIn offic...

2016 limited series published by Marvel Comics Deadpool v. GambitCover of Deadpool v. Gambit #1 (June 2016).Art by Danilo BeyruthPublication informationPublisherMarvel ComicsScheduleMonthlyFormatLimited seriesPublication dateAugust 2016 – November 2016No. of issues5Main character(s)Deadpool, GambitCreative teamWritten byBen Acker, Ben BlackerArtist(s)Danilo BeyruthCollected editionsDeadpool V Gambit: The V is for Vs.ISBN 978-1302901790 Deadpool v. Gambit, also known as Deadpool vs. Gam...

American diplomat & military officer (born 1955) For the Filipino actor, see John Estrada. John EstradaEstrada in 2022United States Ambassador to Trinidad and TobagoIn officeApril 19, 2016[1] – January 20, 2017PresidentBarack ObamaPreceded byMargaret Diop (acting)Succeeded byJoseph Mondello15th Sergeant Major of the Marine CorpsIn officeJune 26, 2003 – April 25, 2007PresidentGeorge W. BushPreceded byAlford L. McMichaelSucceeded byCarlton Kent Personal det...

Commuter rail service in Illinois Milwaukee District North LineEMD F40PH No. 120 leads an outbound train at DeerfieldOverviewService typeCommuter railStatusOperatingLocaleNorthern Chicago metropolitan areaPredecessorMilwaukee RoadCurrent operator(s)MetraRidership23,257 (Avg. Weekday 2014)[1]Annual ridership2,786,215 (2023)RouteTerminiUnion StationFox LakeStops22Distance travelled49.7 miles (80.0 km)Average journey time97 minutes, stopping at all stopsLine(s) usedC&M Subdivisi...

العلاقات البيلاروسية الناوروية روسيا البيضاء ناورو روسيا البيضاء ناورو تعديل مصدري - تعديل العلاقات البيلاروسية الناوروية هي العلاقات الثنائية التي تجمع بين روسيا البيضاء وناورو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية ...

العلاقات اليونانية الكينية اليونان كينيا اليونان كينيا تعديل مصدري - تعديل العلاقات اليونانية الكينية هي العلاقات الثنائية التي تجمع بين اليونان وكينيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة الي�...

克拉拉·舒曼Clara Josephine Schumann克拉拉·舒曼的肖像画,弗朗茨·冯·伦巴赫(英语:Franz von Lenbach)绘于1838年出生(1819-09-13)1819年9月13日德意志邦联萨克森王国莱比锡逝世1896年5月20日(1896歲—05—20)(76歲)德意志帝国法兰克福职业钢琴家、作曲家、钢琴教师知名作品《a小调钢琴协奏曲(英语:Piano Concerto (Clara Schumann))》《g小调钢琴三重奏(英语:Piano Trio (Clara Schumann))》《...

Voce principale: Verein für Laufspiele Sportfreunde Lotte von 1929. Verein für Laufspiele Sportfreunde Lotte von 1929Stagione 2017-2018Sport calcio Squadra Sportfreunde Lotte Allenatore Oscar Corrochano (1ª) Marc Fascher (2ª-14ª) Andreas Golombek (15ª-38ª) All. in seconda Joseph Laumann 3. Liga16º posto Maggiori presenzeCampionato: Heyer, Wendel (34)Totale: Heyer, Wendel (34) Miglior marcatoreCampionato: Oesterhelweg (8)Totale: Oesterhelweg (8) StadioFRIMO Stadion Maggior numero...
Questa voce sugli argomenti società di pallacanestro italiane e Lazio è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Cestistica CivitavecchiaPallacanestro Segni distintiviUniformi di gara Casa Trasferta Colori socialiRosso e nero Dati societariCittàCivitavecchia Nazione Italia CampionatoSerie C Fondazione1948 DenominazioneCestistica Civitavecchia1948 PresidenteStefano Rizzitiello AllenatoreFerdinando Di Maria La Cestistica Civitavecchia è la ...

Religious figure who confronted Peter For the film, see Simon Magus (film). Simon MagusΣίμων ὁ μάγοςRelief of Simon Magus at the gate of the Basilica of Saint-Sernin, Toulouse.TitleMagusPersonalReligionGnosticismNationalitySamaritanKnown forFounder of GnosticismOrganizationFounder ofSimonianism Simon Magus (Greek Σίμων ὁ μάγος, Latin: Simon Magus), also known as Simon the Sorcerer or Simon the Magician, was a religious figure whose confrontation with Peter is...















![{\displaystyle \operatorname {erf} (x)^{2}={\frac {4}{\pi }}\int _{0}^{1}{\frac {1-\exp[-x^{2}(y^{2}+1)]}{y^{2}+1}}\mathrm {d} y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12945ca7903dbb5803328b1c5139cabfc79d9ed4)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)