Ehrenfest-Theorem
|
Read other articles:
Kaltenkirchen Lambang kebesaranLetak Kaltenkirchen di Segeberg NegaraJermanNegara bagianSchleswig-HolsteinKreisSegeberg Pemerintahan • MayorStefan Sünwoldt (SPD)Luas • Total23,1 km2 (89 sq mi)Ketinggian31 m (102 ft)Populasi (2013-12-31)[1] • Total20.080 • Kepadatan87/km2 (230/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos24568Kode area telepon04191Pelat kendaraanSESitus webwww.kaltenkirchen.de Kaltenkirc...
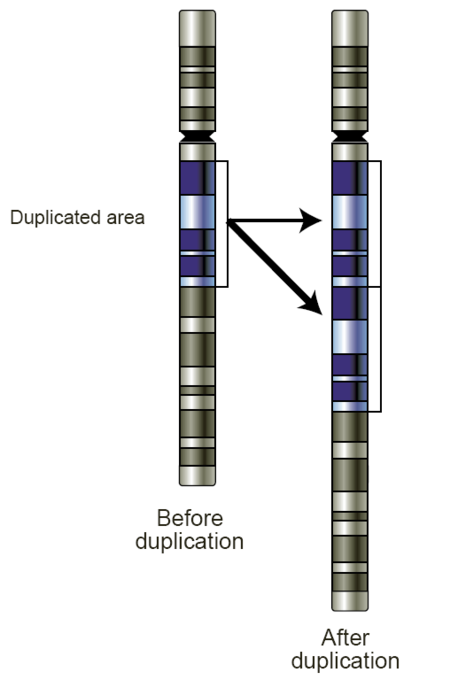
Sebuah skema bagian kromosom sebelum dan sesudah kejadian duplikasi Duplikasi gen (ataupun duplikasi kromosom atau amplifikasi gen) merupakan kejadian bergandanya (duplikasi) suatu daerah bagian DNA yang mengandung gen. Ia dapat terjadi sebagai kesalahan pada rekombinasi homolog, kejadian retrotransposisi, ataupun duplikasi keseluruhan kromosom.[1] Kopi kedua dari gen ini sering kali terbebas dari tekanan seleksi, yakni bahwa mutasi ini tidak memiliki efek merugikan pada organisme ina...

Dewan Perwakilan Rakyat Kota Sabang DPRK Sabang2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai2 September 2019PimpinanKetuaMuhammad Nasir (Partai Aceh) sejak 21 Oktober 2019 Wakil Ketua IArmadi (Demokrat) sejak 21 Oktober 2019 Wakil Ketua IIFerdiansyah (Golkar) sejak 21 Oktober 2019 KomposisiAnggota20Partai & kursi NasDem (1) Demokrat (2) PAN (1) Golkar (2) PBB (2) PKS (1) &#...

Pour les articles homonymes, voir Winter. David Alexandre WinterDavid Alexandre Winter au Concours Eurovision de la chanson 1970.BiographieNaissance 4 avril 1943 (80 ans)AmsterdamNom de naissance Lion KleerekoperNationalité néerlandaiseActivités Auteur-compositeur-interprète, chanteurEnfants Ophélie WinterMickaël Winter (d)Autres informationsLabels Riviera, Barclay, Philips Records, Epic RecordsGenre artistique PopSite web www.david-alexandrewinter.com/en/Home.aspmodifier - modifi...

Dargaz County شهرستان درگز مقاطعة الإحداثيات 37°20′N 59°05′E / 37.333°N 59.083°E / 37.333; 59.083 تقسيم إداري الدولة إيران المحافظة خراسان رضوي عاصمة دركز بلدة (Districts) الناحية المركزية، ناحية تشابشلو، ناحية لطف أباد، Now Khandan District عدد السكان (2006) المجموع 73,439 عدد �...
Mohon bantuanya pak Ivan mohon bantuanya untuk segera memvalidasi halaman Tarekat Naqsyabandiyah versi pending terlalu banyak, dn tampilan halaman yg divlasidasi masih membutuuhkan edit, versi pending setidaknya mendekati artikel yg benar sesuai EYD.. meskipun masih membutuhkan revisi lagi... terima kasih sekiranya bapak berkenan masukan saya. pengguna: Riznaldo Mohon bantuannya Pak Ivan mohon bantuannya untuk validasi suntingan pada artikel yang saya buat Anak Agung Gde Agung kenapa selalu ...

Voce principale: Associazione Sportiva Dilettantistica S.E.F. Tempio Pausania. Unione Sportiva TempioStagione 1993-1994Sport calcio Squadra Tempio Allenatore Giovanni Mialich Presidente Antonello Ganau Serie C28º posto nel girone A. Maggiori presenzeCampionato: De Giorgi, Pittalis (34) Miglior marcatoreCampionato: Pau (6) 1992-1993 1994-1995 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Unione Sportiva Tempio nelle competizioni ufficiali del...

French botanist (1656–1708) Tourn. redirects here. For the medieval legal term, see Tourn. Joseph Pitton de TournefortJoseph Pitton de TournefortBorn5 June 1656Aix-en-Provence, Kingdom of FranceDied28 December 1708 (aged 52)Paris, Kingdom of FranceNationalityFrenchAlma materUniversity of ParisKnown forgenusScientific careerFieldsbotany Joseph Pitton de Tournefort (5 June 1656 – 28 December 1708) was a French botanist, notable as the first to make a clear definition ...

YAPIS di Tanah PapuaJenisYayasanDidirikan15 Desember 1968LokasiJl. Dr. Sam Ratulangi No. 3 Dok V Atas, Kota JayapuraOrang pentingKetua Umum : Dr. Drs. Muhammad Musa'ad, M.Si.Ketua Dewan Pembina :Thaha AlhamidWilayah layananIndonesiaFokusPendidikanSloganAmal Ilmiah dan Ilmu AmaliahSitus resmiwww.yapispapua.org Yayasan Pendidikan Islam di Tanah Papua atau sering disingkat YAPIS adalah yayasan swasta yang bergerak di bidang pendidikan di Kota Jayapura dengan wilayah kerja di seluruh Pu...

Batman NinjaBatman in una scena del filmTitolo originaleニンジャバットマンNinja Battoman Lingua originalegiapponese Paese di produzioneGiappone, Stati Uniti d'America Anno2018 Durata85 min Rapporto1,78:1 Genereanimazione, azione RegiaJunpei Mizusaki SceneggiaturaKazuki Nakashima Produttore esecutivoBenjamin Melniker, Michael E. Uslan Casa di produzioneWarner Bros. Animation, DC Entertainment Distribuzione in italianoWarner Bros. Entertainment Italia MontaggioKiyoshi Hirose Mu...

Japanese real estate developer Mitsui Fudosan Co. Ltd.Native name三井不動産株式会社Romanized nameMitsui Fudōsan kabushiki gaishaCompany typePublic (KK)Traded as TYO: 8801 Nikkei 225 component TOPIX Core30 component IndustryReal estateFoundedJuly 15, 1941; 82 years ago (1941-07-15)HeadquartersMitsui Main Building, 2-1-1 Nihonbashi-Muromachi, Chūō, Tokyo, JapanKey peopleMasanobu Komoda [jp][1] (Chairman)Takashi Ueda [jp] (President...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

American politician For other people with this name, see Theodorick Bland. Theodorick BlandMember of the U.S. House of Representativesfrom Virginia's 9th districtIn officeMarch 4, 1789 – June 1, 1790Preceded byposition establishedSucceeded byWilliam B. GilesDelegate to the Congress of the Confederation from VirginiaIn officeNovember 1, 1780 – October 30, 1783Member of the Virginia House of Delegates from Prince George CountyIn officeOctober 16, 1786 –&...

Football tournament season 1904 German championshipDeutsche FußballmeisterschaftReplica of the Viktoria trophyTournament detailsCountryGermanyDates24 April – 29 MayTeams8Final positionsChampionsNo champion declaredTournament statisticsMatches played6Goals scored36 (6 per match)Top goal scorer(s)Unknown[note 1]← 19031905 → The 1904 German football championship was the second competition to determine the national champion of Germany. The competit...

Martian dune field Abalos Undae dunes at Abalos Scopuli, the scarp of Abalos Mensa. The ice layers on the cap and basal formations are also visible. The picture was taken by the HiRISE camera on board the Mars Reconnaissance Orbiter and was enhanced by NASA in RGB colour. Abalos Undae (Latin for Abalos Waves) is a dune field on Mars in the periphery of Planum Boreum, the Martian North pole. It is one of the officially named northern circumpolar dune fields, along with Olympia, Hyperboreae, an...

Pour les articles homonymes, voir San Luis. Cet article est une ébauche concernant une localité argentine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. San Luis del Palmar Héraldique Administration Pays Argentine Province Corrientes Département San Luis del Palmar Maire Vicente Ramón Romero Code postal W3403 Indicatif téléphonique 3783 Démographie Gentilé Sanluiseño Population 13 895 ...

Byzantine imperial guards ExcubitorsActivec. 460 CE – c. 1081CountryByzantine EmpireTypeImperial guard (mid-5th – 7th centuries), heavy cavalry (mid-8th – 11th centuries)Garrison/HQConstantinople (5th–8th centuries), Bithynia and Thrace (8th–11th centuries), provincial detachments at least in Longobardia and Hellas (10th–11th centuries)EngagementsMaurice's Balkan campaigns of 582-602 Heraclius' campaigns during the Byzantine–Sasanian War of 602–628, Abbasid invasio...

Disambiguazione – Se stai cercando altri significati, vedi Pianoforte (disambigua). Questa voce o sezione sull'argomento Musica è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i sug...

«Siamo un corpo solo: banditi, polizia e mafia! Come il Padre, il Figlio e lo Spirito Santo!» (Gaspare Pisciotta al Processo di Viterbo)Gaspare Pisciotta (a sin.) assieme a Salvatore Giuliano Gaspare Pisciotta (Montelepre, 5 marzo 1924 – Palermo, 9 febbraio 1954) è stato un criminale italiano, personaggio della storia criminale siciliana del secondo dopoguerra. Indice 1 Biografia 1.1 L'arresto e la morte di Giuliano 1.2 Il processo di Viterbo 1.3 Il carcere e l'avvelenamento 2 Influenza...

لمعانٍ أخرى، طالع دليلة (توضيح). دليلةملصق الفيلممعلومات عامةالصنف الفني استعراضي رومانسيتاريخ الصدور 15 أكتوبر 1956مدة العرض 125 دقيقةاللغة الأصلية لغة عربية (مصرية)العرض أبيض وأسود البلد مصرالطاقمالمخرج محمد كريمالقصة علي أمينالحوار علي أمينالسيناريو علي أمينال...

![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\langle O\rangle ={\frac {1}{\mathrm {i} \hbar }}\langle [O,H]\rangle +\left\langle {\frac {\partial O}{\partial t}}\right\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec2ade83874cd40604c622067ff728ef61504069)










![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\langle O\rangle ={\frac {1}{\mathrm {i} \hbar }}\langle \psi |OH|\psi \rangle -{\frac {1}{\mathrm {i} \hbar }}\langle \psi |HO|\psi \rangle +\left\langle {\frac {\partial O}{\partial t}}\right\rangle ={\frac {1}{\mathrm {i} \hbar }}\langle [O,H]\rangle +\left\langle {\frac {\partial O}{\partial t}}\right\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/17cd4ad1bba2c0a982b0edbb5a2ad638728f4b4a)

![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\langle p\rangle ={\frac {i}{\hbar }}\langle [H,p]\rangle ={\frac {i}{\hbar }}\langle [{\frac {p^{2}}{2m}}+V(x),p]\rangle ={\frac {i}{\hbar }}\langle [V(x),p]\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ad2efd5aa4285d3d732e995c347093d6cc99ffe)
![{\displaystyle [V,p]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e460d1143a21ad534084b644c7781dc30069fe37)



![{\displaystyle [V,-i\hbar \nabla ]\Psi =-i\hbar V\nabla \Psi -(-i\hbar \nabla (V\Psi ))=-i\hbar V\nabla \Psi +i\hbar (\nabla V)\Psi +i\hbar V(\nabla \Psi )=i\hbar (\nabla V)\Psi \quad \Rightarrow \quad [V,p]=i\hbar (\nabla V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e7accd7efbbde1e74f0c9371b9cd336ceb32f6d)

![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\langle x\rangle ={\frac {i}{\hbar }}\langle [H,x]\rangle ={\frac {i}{\hbar }}\langle [{\frac {p^{2}}{2m}}+V(x),x]\rangle ={\frac {i}{\hbar }}{\frac {1}{2m}}\langle [p^{2},x]\rangle ={\frac {i}{\hbar }}{\frac {1}{2m}}\langle p\underbrace {[p,x]} _{-i\hbar }+\underbrace {[p,x]} _{-i\hbar }p\rangle ={\frac {1}{m}}\langle p\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/554b1e671e15efabd5e6ebbfc93052c4398ade78)
![{\displaystyle [p^{2},x]=p[p,x]+[p,x]p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b21a0e268c2f9c5021505c16539d3e72749d7b0)










