Auflösung (Blockplan)
|
Read other articles:

Gusti SholihinLahir(1925-06-05)5 Juni 1925Banjarmasin, Hindia-BelandaMeninggal15 Februari 1961(1961-02-15) (umur 35)Denpasar, BaliPekerjaanPelukisOrganisasiTunas Pelukis Muda Gusti Sholihin (7 Juni 1925 – 15 Februari 1961) adalah seorang pelukis Indonesia. Ia juga salah satu perintis pertama Akademi Seni Rupa Indonesia (ASRI).[1] Bersama pelukis Affandi dan Kusnadi, karyanya sempat ditampilkan di Sao Paulo, Brazil, Belanda, Paris, dan New Delhi sekitar tahun 1953...
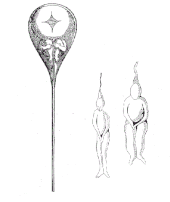
Representation of a small human being, common in alchemy and fiction For other uses, see Homunculus (disambiguation). A homunculus (UK: /hɒˈmʌŋkjʊləs/ hom-UNK-yuul-əs, US: /hoʊˈ-/ hohm-, Latin: [hɔˈmʊŋkʊlʊs]; little person, pl.: homunculi UK: /hɒˈmʌŋkjʊliː/ hom-UNK-yuul-ee, US: /hoʊˈ-/ hohm-, Latin: [hɔˈmʊŋkʊli]) is a small human being.[1] Popularized in sixteenth-century alchemy and nineteenth-century fiction, it has historically referred t...

Ernei NagyernyeDesaNegara RumaniaCountyCounty MureşPemerintahan • Wali kotaFerenc Jánosi (Uni Demokratik Hungaria di Rumania)Populasi (2011) • Total5.835Zona waktuUTC+2 (EET) • Musim panas (DST)UTC+3 (EEST) Ernei (Hongaria: Nagyernyecode: hu is deprecated ; pelafalan: [nɒɟɛrɲɛ] ) adalah sebuah komune yang terletak di County Mureş, Transilvania, Rumania. Menurut sensus pada tahun 2002, komune ini memiliki jumlah penduduk sebesar 5.835 jiwa,...

Bola voli pada Pekan Olahraga Nasional 2021, LokasiGOR Bolavoli, Koya Koso, Kota Jayapura, Papua (Indoor)GOR Voli Pasir Koya Koso, Kota Jayapura, Papua (Pantai/Pasir)Tanggal30 September-12 Oktober 2021 (Indoor)Pantai 1-11 Oktober 2021 (Pantai/Pasir)← 20162024 → Bola voli pada Pekan Olahraga Nasional 2021 akan digelar dari 30 September sampai 12 Oktober 2021 di GOR Bolavoli, Koya Koso, Kota Jayapura, Papua. Pertandingan kali ini menampilkan 4 nomor, masing masing untuk pu...

Hal Ashby (2 September 1929-27 Desember 1988) merupakan seorang sutradara berkebangsaan Amerika Serikat yang memenangkan Academy Award. Dia dilahirkan di Ogden, Utah dengan nama William Hal Ashby. Dia berkarier di dunia film sejak tahun 1970. Filmografi The Landlord (1970) Harold and Maude (1971) The Last Detail (1973) Shampoo (1975) Bound for Glory (1976) Coming Home (1978) Being There (1979) Second-Hand Hearts (1981) Lookin' to Get Out (1982) Let's Spend the Night Together (1983) The Slugge...

Peta infrastruktur dan tata guna lahan di Komune Grandrupt. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiGrandrupt merupakan sebuah komune di departemen Vosges yang terletak pada sebelah timur laut Prancis. Lihat pula Komune di departemen Vosges Referensi INSEE Diarsipkan 2007-11-24 di Wayback Machine. lbsKomune di departemen Vosges Les Ableuvenettes Ahéville A...

Attic theatre performance related to both comedy and tragedy A drinking cup, c. 490–480 B.C., depicting a maenad and a satyr. The satyr play is a form of Attic theatre performance related to both comedy and tragedy. It preserves theatrical elements of dialogue, actors speaking verse, a chorus that dances and sings, masks and costumes. Its relationship to tragedy is strong; satyr plays were written by tragedians, and satyr plays were performed in the Dionysian festival following the performa...

Pour une institution plus récente, voir Sénat de la République (Italie). Politique dans la Rome antique Données clés Royauté romaine753 – 509 av. J.-C. République romaine509 – 27 av. J.-C. Empire romain27 av. J.-C. – 476 Principat27 av. J.-C. – 285 Dominat285 – 476 Emp. d'Occident395 – 476 Emp. byzantin395 – 1453 MagistraturesCursus honorum Magistrats ordinaires Tribun de la plèbe QuesteurÉdilePréteur Tr. consulaireConsulCenseur Promagistrats Propréteur Pro...

Area where land meets the sea or ocean For other uses, see Coast (disambiguation). Shore and Shoreline redirect here. For other uses, see Shore (disambiguation) and Shoreline (disambiguation). Sunrise on the Jersey Shore coastline at Spring Lake, New Jersey, U.S. Rugged coastline of the West Coast Region of New Zealand Southeast coast of Greenland Escorca coast, Serra de Tramuntana (Balearic Islands) The coast, also known as the coastline, shoreline or seashore, is defined as the area where l...

Эта статья или раздел нуждается в переработке.Пожалуйста, улучшите статью в соответствии с правилами написания статей. Марш «в защиту жизни». Прага, 2006 год Демонстрация «Важна каждая жизнь» в Мадриде, Испания, 17 октября 2009 года. Прола́йф, или движение «в защиту жизни...

Treffieuxcomune (dettagli) Treffieux – Veduta LocalizzazioneStato Francia Regione Paesi della Loira Dipartimento Loira Atlantica ArrondissementChâteaubriant CantoneGuémené-Penfao TerritorioCoordinate47°37′N 1°32′W / 47.616667°N 1.533333°W47.616667; -1.533333 (Treffieux)Coordinate: 47°37′N 1°32′W / 47.616667°N 1.533333°W47.616667; -1.533333 (Treffieux) Superficie18,97 km² Abitanti765[1] (2009) Densità40,33 ab...

إبراهيم بن عبد الجليل التبريزي (بالفارسية: ابراهیم بن عبدالجلیل سپهسالار تبریزی) معلومات شخصية الميلاد تبريز الوفاة العقد 1830 كربلاء مواطنة الدولة القاجارية الديانة الإسلام[1]، وشيعة اثنا عشرية[1] الحياة العملية تعلم لدى أحمد بن زين الدين ا�...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Pasar Muara BungoKecamatanSalah satu sudut Pasar Muara BungoNegara IndonesiaProvinsiJambiKabupatenBungoPemerintahan • CamatZenhendri B, S.Sos., M.SiPopulasi (2019) • Total27.696 jiwaKode pos37214Kode Kemendagri15.08.03 Kode BPS1509024 Desa/kelurahan5 kelurahan Jembatan Batang Bungo sekitar tahun 1930-an Pasar Muara Bungo adalah sebuah kecamatan di Kabupaten Bungo, Provinsi Jambi, Indonesia. Berdiri berdasarkan Perda No.12 tahun 2005 tentang perubahan nama kec...

Borough in Somerset County, New Jersey, US Borough in New Jersey, United StatesSomerville, New JerseyBoroughSomerset County CourthouseDaniel Robert House – Borough Hall and Public LibraryLocation of Somerville in Somerset County highlighted in yellow (right). Inset map: Location of Somerset County in New Jersey highlighted in black (left).Census Bureau map of Somerville, New Jersey Interactive map of Somerville, New JerseySomervilleLocation in Somerset CountyShow map of Somerset County, New...

Private university in Seoul and Suwon, South Korea For the former Confucian academy, see Sungkyunkwan. For the subway station by the Natural Sciences Campus, see Sungkyunkwan University Station. For the university in North Korea, see Koryo Songgyungwan University. Sungkyunkwan University成均館大學校성균관대학교[1]Motto仁義禮智인의예지Motto in EnglishHumanity, Righteousness, Propriety, Wisdom[2]TypePrivateEstablished1398; 626 years ago ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Gambaran haseki penjaga Sultan Hadji Ali Haseki (bahasa Turki: Hacı Ali Haseki, bahasa Yunani: Χατζή Αλής Χασεκής) merupakan penguasa Atena asal Turki Usmani dari abad ke-XVIII, ia memerintah selama dua puluh tahun (1775–1795...

American reality television series Kingin' with TygaGenreReality televisionStarring Tyga Country of originUnited StatesOriginal languageEnglishNo. of seasons2No. of episodes12ProductionExecutive producers Tyga Anthony Martin Marcus Fox Todd Nelson J.D. Roth Brant Pinvidic Adam Kaloustian Elena Diaz Karen Frank Darin Byrne Paul Ricci Chris McCarthy Camera setupMultipleRunning time22 minutesProduction company3 Ball EntertainmentOriginal releaseNetwork MTV2 MTV ReleaseJuly 24, 2015 (2015-07...

日本 > 千葉県 > 我孫子市 > 日の出 (我孫子市) 日の出 大字 日の出日の出の位置 北緯35度52分58.9秒 東経140度3分24.7秒 / 北緯35.883028度 東経140.056861度 / 35.883028; 140.056861国 日本都道府県 千葉県市町村 我孫子市標高 6 m人口(2017年(平成29年)4月1日現在)[1] • 合計 0人等時帯 UTC+9 (日本標準時)郵便番号 270-1174[2]市外局�...

Rhode Island Thoroughbred track (1934–1978) This article is about the 20th-century Thoroughbred track. For the 19th-century harness track, see Narragansett Park (1867–1924). Narragansett ParkNarragansett Park Post Card photo circa 1950s.LocationPawtucket, Rhode IslandCoordinates41°51′40″N 71°20′45″W / 41.86111°N 71.34583°W / 41.86111; -71.34583Date openedAugust 1, 1934Date closedSeptember 4, 1978Race typeThoroughbred racingCourse typeFlatNotable racesNa...





























