Äußerer Weißenbach
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Jacob WohlWohl pada Agustus 2020Lahir12 Desember 1997 (umur 26)Los Angeles, California, Amerika SerikatDikenal atasKlaim palsu terhadap figur-figur politikOrang tuaDavid Wohl (bapak)Situs webjacobwohl.org Jacob Wohl (lahir 12 Desember 1997) adala...

Connie SutedjaConnie di Madjalah Aktuil Edisi 37 Tahun 1969LahirSukarni10 November 1944 (umur 79)Tasikmalaya, Masa Pendudukan JepangNama lainConnie SutedjaPekerjaanPemeranmodelTahun aktif1965—sekarangAnak1 Sukarni binti Sutedja (lahir 10 November 1944), lebih dikenal sebagai Connie Sutedja[1] adalah pemeran dan model Indonesia. Ia merupakan salah satu dari empat anggota Golden Girls bersama Nani Widjaja, Ida Kusumah dan Rina Hassim. Pada awal karirnya sebagai pemain ...

العلاقات الأرجنتينية الرواندية الأرجنتين رواندا الأرجنتين رواندا تعديل مصدري - تعديل العلاقات الأرجنتينية الرواندية هي العلاقات الثنائية التي تجمع بين الأرجنتين ورواندا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتي�...

Maritime special forces unit Naval Diving UnitLogo of the Naval Diving UnitActive12 December 1971 – presentCountry SingaporeBranch Republic of Singapore NavyTypeSpecial forcesRoleSpecial operationsDirect actionExplosive ordnance disposalUnderwater demolitionHostage rescueCounter-terrorismSize6 squadronsPart ofSpecial Operations Task ForceGarrison/HQSembawang CampNickname(s)Warriors of the Deep, Frogmen, Frogmen from the SeaMotto(s)Nothing Stands In Our WayEngagements See list...
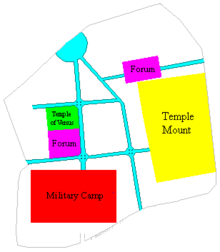
Il Spasimo, Yesus memanggul salib-Nya di Via Dolorosa, karya Raphael, 1516 Via Dolorosa (bahasa Latin untuk Jalan Kesengsaraan atau Jalan Penderitaan; bahasa Inggris: Way of Grief, Way of Sorrow, Way of Suffering atau Painful Way; bahasa Ibrani: ויה דולורוזה; bahasa Arab: طريق الآلام) adalah sebuah jalan di Kota Yerusalem Kuno. Jalan ini diyakini adalah jalan yang dilalui Yesus sambil memanggul salib menuju Kalvari. Jalur yang berkelok-kelok dari benteng Antonia ke arah b...

Hotel resort complex near Walt Disney World in Florida, United States Wyndham Resort Bonnet Creek Map in relation to Walt Disney World Bonnet Creek Resort is a development in the southeast corner of Walt Disney World. The land, which is not owned by Disney, is bordered on three sides by Disney-owned land and on the fourth side by Interstate 4. It is surrounded by the Bonnet Creek nature preserve and is named after Bonnet Creek, which runs through the property. The entrance is located on Buena...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

Greek cruise company between 1984-1985 This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (June 2023) (Learn how and when to remove this message) The neutrality of this articl...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

A light curve for Spica, adapted from Tkachenko et al. (2016)[1] Rotating ellipsoidal variables are a class of close binary variable star systems whose components are ellipsoidal. They are not eclipsing, but fluctuations in apparent magnitude occur due to changes in the amount of light emitting area visible to the observer. Typical brightness fluctuations do not exceed 0.1 magnitudes.[2] The brightest rotating ellipsoidal variable is Spica (α Virginis).[3] List of var...

العلاقات الصومالية السورية الصومال سوريا الصومال سوريا تعديل مصدري - تعديل العلاقات الصومالية السورية هي العلاقات الثنائية التي تجمع بين الصومال وسوريا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة الص�...

Pour le film, voir Les Troyennes (film). Les TroyennesAstianaxTitre original (grc) ΤρῳάδεςFormats Pièce de théâtreŒuvre dramatique (d)Langue Grec ancienAuteur EuripideGenre Tragédie grecquePersonnages Athéna (d)Hécube (d)Cassandre (d)Talthybios (d)Andromaque (d)Œuvre dérivée The Trojan Women today (d)modifier - modifier le code - modifier Wikidata Les Troyennes (en grec : Τρῳάδες / Trōiádes) est une tragédie d’Euripide, représentée pour la première...

Фалафель Табули Фаттуш Ливанская кухня, (араб. المأكولات اللبنانية) — национальная кухня Ливана, типичная средиземноморская кухня. Для неё характерны разнообразие вегетарианских блюд, использование приправ и таких продуктов как бобовые (боб обыкновенный, нут), св...

Questa voce sull'argomento centri abitati del Paraná è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Jardim Olindacomune LocalizzazioneStato Brasile Stato federato Paraná MesoregioneNoroeste Paranaense MicroregioneParanavaí AmministrazioneSindacoJuraci Paes da Silva TerritorioCoordinate22°33′06″S 52°02′15″W22°33′06″S, 52°02′15″W (Jardim Olinda) Altitudine331 m s.l.m. Superficie128,51 km² Abitanti1 409...

English lawyer and judge Sir Edward Ward (1638–1714) was an English lawyer and judge. He became chief baron of the exchequer, and is best known as the judge in the state trial for piracy of Captain Kidd. Sir Edward Ward, 1702 engraving by Robert White. Life Born in June 1638, he was the second son of William Ward of Preston, Rutland. He was educated under Francis Meres at Wing, Rutland. He was a student at Clifford's Inn, and was then admitted in June 1664 at the Inner Temple; he was called...

Questa voce sull'argomento storia del Giappone è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Questa voce o sezione sull'argomento storia del Giappone non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Mappa delle province giapponesi con la provincia di Iwami evidenziata Iwami (石見国; Iwami no kuni) fu una provi...

Cet article est une ébauche concernant une localité italienne et le Piémont. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Margarita. Margarita Administration Pays Italie Région Piémont Province Coni Code postal 12040 Code ISTAT 004118 Code cadastral E945 Préfixe tel. 0171 Démographie Population 1 450 hab. (31-12-2010[1]) Densité 132 hab./km2...

Part of mathematics that addresses the stability of solutions For the branch of model theory, see stable theory. Stability diagram classifying Poincaré maps of linear autonomous system x ′ = A x , {\displaystyle x'=Ax,} as stable or unstable according to their features. Stability generally increases to the left of the diagram.[1] Some sink, source or node are equilibrium points. In mathematics, stability theory addresses the stability of solutions of differential equations and...

US Open 1981Sport Tennis Data1º settembre - 13 settembre Edizione101ª CategoriaGrande Slam (ITF) SuperficieCemento LocalitàNew York negli Stati Uniti ImpiantoUSTA Billie Jean King National Tennis Center, Flushing Meadows CampioniSingolare maschile John McEnroe Singolare femminile Tracy Austin Doppio maschile Peter Fleming / John McEnroe Doppio femminile Anne Smith / Kathy Jordan Doppio misto Anne Smith / Kevin Curren 1980 1982 Lo US Open 1981 è stata la 101ª edizione dello US Open e quar...

Method for increasing reliability For other uses of TMR, see TMR (disambiguation). Triple Modular Redundancy. Three identical logic circuits (logic gates) are used to compute the specified Boolean function. The set of data at the input of the first circuit are identical to the input of the second and third gates. In computing, triple modular redundancy, sometimes called triple-mode redundancy,[1] (TMR) is a fault-tolerant form of N-modular redundancy, in which three systems perform a ...
