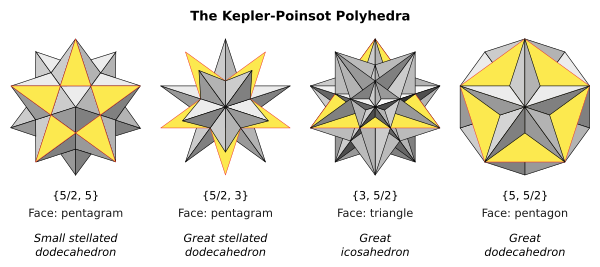
Políedre de Kepler-Poinsot
|
Read other articles:

Pemandangan di puncak pegunungan Titiwangsa Pegunungan Titiwangsa (bahasa Melayu: Banjaran Titiwangse) adalah jajaran pegunungan yang membentuk tulang punggung Semenanjung Malaya. Jajaran ini dimulai di utara di Thailand Selatan dan berakhir di selatan dekat Johor Utara, Malaysia. Dengan titik tertingginya 2.183 m di Gunung Korbu, pegunungan ini menjadi batas alami alternatif antara Asia Tenggara dan Melanesia selain Sungai Kolok dan Sungai Perlis. Puncak gunung tertinggi di pegunungan ini ad...

Untuk kelas kapal penjelajah Austro-Hungaria dengan nama yang sama, lihat Kapal penjelajah kelas Zara (1879). Kapal penjelajah berat kelas Zara Kapal penjelajah Italia Zara Tentang kelas Nama:Kelas ZaraOperator: Regia MarinaDidahului oleh:Kapal penjelajah kelas-TrentoDigantikan oleh:BolzanoDibangun:1929-1932Bertugas:1931-1944Selesai:4Hilang:4 Ciri-ciri umum Kelas dan jenis Kapal penjelajah beratBerat benaman 11.326 hingga 11.712 ton panjang (11.508 hingga 11.900 t) (standar) 13...

العلاقات الغامبية الميكرونيسية غامبيا ولايات ميكرونيسيا المتحدة غامبيا ولايات ميكرونيسيا المتحدة تعديل مصدري - تعديل العلاقات الغامبية الميكرونيسية هي العلاقات الثنائية التي تجمع بين غامبيا وولايات ميكرونيسيا المتحدة.[1][2][3][4][5] مق...

AkuntansiKonsep dasarAkuntan · Pembukuan · Neraca percobaan · Buku besar · Debit dan kredit · Harga pokok · Pembukuan berpasangan · Standar praktik · Basis kas dan akrual · PABU / IFRSBidang akuntansiBiaya · Dana · Forensik · Keuangan · Manajemen · PajakLaporan keuanganNeraca · Laba rugi · Perubahan ekuitas · ...

Orhan Ghaziاورخان غازیBeyGhaziPemimpin UtsmaniyahBerkuasa1323/4 ‒ Maret 1362PendahuluOsman IPenerusMurad IInformasi pribadiKelahiran1281SöğütKematianMaret 1362(umur 80–81)BursaPemakamanOrhan Ghazi Türbe, Gümüşlü Kümbet, BursaWangsaUtsmaniyahAyahOsman I, pemimpin UtsmaniyahIbuRabia Bala Hatun atau Malhun HatunPasanganNilüfer HatunAsporça HatunTheodora Kantakouzene HatunEftandise HatunAgamaSunni IslamTughra Orhan Ghazi (Turki Otoman: اورخان غازی, Orhan Gha...

WarnerMedia WarnerMedia, LLC. 30 Hudson Yards, sede de WarnerMedia en la ciudad de Nueva YorkTipo FilialIndustria Medio de comunicación de masasForma legal Sociedad de responsabilidad limitadaFundación 10 de febrero de 1972Fundador Steve Ross(para la línea Warner Communications; primer CEO)Ted Turner(para la línea Turner Broadcasting System)Disolución 8 de abril de 2022Nombres anteriores Warner Communications Inc.(1972-1990)Time Warner(1990-2001; 2003-2018)Time Warner Entertainment(1992�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of Hindi films of 1982 – news · newspapers · books · scholar · JSTOR (July 2020) (Learn how and when to remove this template message) Hindi cinema 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 193...

L’heroic fantasy ou le sword and sorcery, qui est parfois traduit en français par merveilleux héroïque ou médiéval fantastique, est un sous-genre littéraire de la fantasy qui présente un récit héroïque dans le cadre d'un monde merveilleux. Définition L'heroic fantasy ou sword and sorcery[notes 1] est la version contemporaine des contes merveilleux de l'Antiquité et du Moyen Âge[1],[2]. Le terme heroic fantasy est inventé en 1967 par l'écrivain américain Lyon Sprague de Camp...

Suburb of Melbourne, Victoria, AustraliaBayswaterMelbourne, VictoriaMountain Highway, BayswaterBayswaterCoordinates37°50′35″S 145°16′05″E / 37.843°S 145.268°E / -37.843; 145.268Population12,262 (2021 census)[1] • Density1,530/km2 (3,970/sq mi)Postcode(s)3153Area8 km2 (3.1 sq mi)Location 27 km (17 mi) from Melbourne 5 km (3 mi) from Croydon LGA(s)City of KnoxState electorate(s)BayswaterFederal...

Final Pharaoh of Theban seventeenth dynasty of Egypt KamoseSarcophagus of Kamose, Cairo Egyptian MuseumPharaohReignc. 1555–1550 BC[1]PredecessorSeqenenre TaoSuccessorAhmose IRoyal titulary Horus name Khahernesetef Ḫˁj-ḥr-nst=f He who appears on his throne Sedjefatawy Sḏf3-t3wj He who nourishes the two lands[2] Neferkhabtawi Nfr-ẖ3b-t3wj The perfect horus who tames the two lands [3] Nebty name Wehem-menu Wḥm-mnw He who renews the fortifications Golden H...

Progress and Poverty Sampul edisi 1881PengarangHenry GeorgeNegaraAmerika SerikatBahasaInggrisSubjekKapitalisme, sosialisme, Georgisme, kebijakan pajak, lahan, rent ekonomiTanggal terbit1879Jenis mediaCetakan (Sampul keras)Halaman406ISBNISBN 1-59605-951-6 Progress and Poverty: An Inquiry into the Cause of Industrial Depressions and of Increase of Want with Increase of Wealth: The Remedy adalah sebuah buku 1879 karya pakar teori sosial dan ekonomi Henry George Progress and Poverty ada...

For other Pennsylvania townships with similar names, see Salisbury Township, Pennsylvania (disambiguation). Township in Pennsylvania, United StatesSalisbury TownshipTownshipSalisbury Township Office in June 2015 SealLocation of Salisbury Township in Lehigh County, PennsylvaniaSalisbury TownshipLocation of Salisbury Township in PennsylvaniaShow map of PennsylvaniaSalisbury TownshipLocation in the United StatesShow map of the United StatesCoordinates: 40°34′46″N 75°30′09″W / ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Star Channel Spanish TV channel – news · newspapers · books · scholar · JSTOR (December 2022) (Learn how and when to remove this message) Television channel Star ChannelCountrySpainBroadcast areaSpain, Andorra, Morocco, Algeria, Gibraltar, Equatorial Guine...

Device that detects smoke, typically as an indicator of fire Smoke detector mounted on a ceiling A smoke detector is a device that senses smoke, typically as an indicator of fire. Smoke detectors/Alarms are usually housed in plastic enclosures, typically shaped like a disk about 150 millimetres (6 in) in diameter and 25 millimetres (1 in) thick, but shape and size vary. Smoke can be detected either optically (photoelectric) or by physical process (ionization). Detectors may use one ...

Para otros usos de este término, véase New York, New York (desambiguación). «New York, New York» Canción de Liza Minnelli, Frank Sinatra, Jan Malmsjö y Christer SjögrenÁlbum New York, New YorkPublicación 1977Género jazzDiscográfica Capitol RecordsProductor(es) Sonny BurkeIdioma original inglésPaís de origen Estados Unidos[editar datos en Wikidata] Liza Minnelli. New York, New York es una canción compuesta por John Kander y Fred Ebb en 1977 para la película homónima...

Voce principale: Campionato mondiale di calcio 1974. Finale del campionato mondiale di calcio 1974I tedeschi occidentali Wolfgang Overath e Gerd Müller sollevano la coppa FIFAInformazioni generaliSport Calcio Competizione1974 FIFA World Cup knockout stage Data7 luglio 1974 CittàMonaco di Baviera ImpiantoStadio Olimpico Spettatori75 200 Dettagli dell'incontro Paesi Bassi Germania Ovest 1 2 Arbitro Jack Taylor (Inghilterra) Successione ← Finale del campionato mondiale di calc...

1966 studio album by the Beatles RevolverStudio album by the BeatlesReleased5 August 1966 (1966-08-05)Recorded6 April – 21 June 1966StudioEMI, LondonGenre Rock pop psychedelia R&B[1] Length35:01Label Parlophone Capitol ProducerGeorge MartinThe Beatles chronology Rubber Soul(1965) Revolver(1966) A Collection of Beatles Oldies(1966) The Beatles North American chronology Yesterday and Today(1966) Revolver(1966) Sgt. Pepper's Lonely Hearts Club Band(1967) Singles ...

Chief officer of the executive branch of a government Not to be confused with Head of state. Executive heads of government, from left to right, top to bottom: Olaf Scholz, Chancellor of Germany Fumio Kishida, Prime Minister of Japan Narendra Modi, Prime Minister of India Giorgia Meloni, Prime Minister of Italy Justin Trudeau, Prime Minister of Canada Sheikh Hasina, Prime Minister of Bangladesh Abiy Ahmed, Prime Minister of Ethiopia Keith Rowley, Prime Minister of Trinidad and Tobago Fiamē Na...

Major Zoroastrian sacred fire The ruins of Takht-e Soleymān, where the fire of Adur Gushnasp was stored. Part of a series onZoroastrianism Primary topics Ahura Mazda Zarathustra Asha Vohu Manah Persia/Iran Faravahar Avestan Divine entities Amesha Spentas Yazatas Ahuras Daevas Fravashi Angra Mainyu Scripture and worship Zoroastrian literature Avesta Ashem Vohu Ahuna Vairya Yenghe hatam Airyaman ishya Fire Temples 101 Names of Ahura Mazda Adur Burzen-Mihr Adur Farnbag Adur Gushnasp Cypress of ...

The five boroughs: 1: Manhattan, 2: Brooklyn, 3: Queens, 4: The Bronx, 5: Staten Island The neighborhoods in New York City are located within the five boroughs of the City of New York. Their names and borders are not officially defined, and they change from time to time.[1] Boroughs Main article: Boroughs of New York City New York City is split up into five boroughs: the Bronx, Brooklyn, Manhattan, Queens, and Staten Island. Each borough has the same boundaries as a county of the sta...