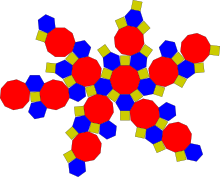
Icosidodecàedre truncat
| |||||||||||||||||||||||||||||||||
Read other articles:

Disambiguazione – Zelensky rimanda qui. Se stai cercando altri significati, vedi Zelensky (disambigua). Volodymyr Zelens'kyj Володимир Зеленський 6º Presidente dell'UcrainaIn caricaInizio mandato20 maggio 2019 Capo del governoVolodymyr HrojsmanOleksij HončarukDenys Šmyhal' PredecessorePetro Porošenko Dati generaliPartito politicoServitore del Popolo Titolo di studioLaurea in giurisprudenza UniversitàUniversità Economica Nazionale di Kiev...

Girator atau pembalik impedansi positif adalah sebuah sirkuit elektronik yang membalikkan impedansi. Dengan kata lain, membuat sirkuit kapasitif menjadi bersifat induktif, tapis lulus-jalur menjadi tapis stop-jalur, dan sebagainya. Ini digunakan terutama pada desain filter aktif dan pengompakan sirkuit. Induktor tersimulasi Sebuah contoh girator yang mensimulasikan induktansi, dengan rangkaian ekivalen dibawahnya. Fungsi utama dari girator adalah untuk mensimulasi unsur induktif pada sirkuit ...

Daryal-type radar (Rusia: Дарьял) (NATO: Pechora) adalah sebuah radar bistatic bertahap-array peringatan dini Soviet. Ini terdiri dari dua antena besar array bertahap yang terpisah aktif dipisahkan oleh sekitar 500 meter (1.640 kaki) 1,5 kilometer (4.921 ft). Pemancar array 30x40 m (98x131 ft) dan penerima dalam ukuran adalah 80x80 m (262x252 kaki). Sistem ini adalah sistem VHF beroperasi pada panjang gelombang 1,5 hingga 2 meter (150 sampai 200 MHz). Kapasitas transmisi awal...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Dejan Stojanovic Informasi pribadiNama lengkap Dejan StojanovicTanggal lahir 19 Juli 1993 (umur 30)Tempat lahir Feldkirch, AustriaTinggi 1,96 m (6 ft 5 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini Crotone (pinjaman d...

Olimje Castle Olimje Castle (Slovene: Grad Olimje) is a 16th-century castle located in the settlement of Olimje, part of the Municipality of Podčetrtek in eastern Slovenia.[1] It is currently a Franciscan monastery.[2] History The predecessor of the current castle occupied the site since c. 1000, and first belonged to the counts von Peilestein (known locally as Pilštajn), including Hemma of Gurk (Slovene: Sv. Ema Krška), an 11th-century saint and member of the family. Aroun...

2014 United States House of Representatives elections in Hawaii ← 2012 November 4, 2014 2016 → All 2 Hawaii seats to the United States House of Representatives Majority party Minority party Party Democratic Republican Last election 2 0 Seats won 2 0 Seat change Popular vote 235,400 120,084 Percentage 65.36% 33.34% Swing 2.09% 0.79% Democratic 50–60% 80–90% Elections in Hawaii Federal government Presidentia...

YayatiययातिTokoh dalam mitologi HinduNamaYayatiEjaan DewanagariययातिEjaan IASTYayātiKitab referensiMahabharata, PuranaKediamanKandhawaprasthaKastakesatriaProfesiRajaDinastiCandraAyahNahusaIbuAsokasundariIstriDewayani dan SarmistaAnakDari Dewayani: Yadu dan Turwasu.Dari Sarmista: Druhyu, Anu, dan Puru. Yayati (Dewanagari: ययाति; ,IAST: Yayāti, ययाति), menurut mitologi dan legenda India, adalah leluhur Maharaja Bharata, penguasa India. Ia meru...

American racing cyclist Evelyn StevensStevens at the 2016 La Flèche Wallonne FémininePersonal informationFull nameEvelyn Lee StevensBorn (1983-05-09) May 9, 1983 (age 40)Claremont, CaliforniaHeight1.65 m (5 ft 5 in)[1]Weight56 kg (123 lb) (2012)[1]Team informationCurrent teamRetiredDisciplineRoadRoleRiderRider typeAll-rounderProfessional teams2010–2014Team HTC–Columbia Women2015–2016Boels–Dolmans[2] Major winsStage...

Women's team kata at the 2023 World Karate ChampionshipsVenueLászló Papp Budapest Sports ArenaLocationBudapest, HungaryDates26, 29 OctoberNations21Teams21Medalists Saori IshibashiChiho MizukamiSae Taira Japan Terryana D'OnofrioMichela RizzoElena Roversi Italy Paola GarcíaMaría LópezGema MoralesRaquel Roy Spain Asmaa AllamNoha Amr AntarAya Hesham Egypt← 20212025 → 2023 World Karate Championshi...

Treffieuxcomune (dettagli) Treffieux – Veduta LocalizzazioneStato Francia Regione Paesi della Loira Dipartimento Loira Atlantica ArrondissementChâteaubriant CantoneGuémené-Penfao TerritorioCoordinate47°37′N 1°32′W / 47.616667°N 1.533333°W47.616667; -1.533333 (Treffieux)Coordinate: 47°37′N 1°32′W / 47.616667°N 1.533333°W47.616667; -1.533333 (Treffieux) Superficie18,97 km² Abitanti765[1] (2009) Densità40,33 ab...
Sporting event delegationPhilippines at the2023 ASEAN Para GamesIPC codePHINPCParalympic Committee of the Philippinesin Phnom PenhCompetitors174 in 13 sportsFlag bearerAriel Joseph Alegarbes (Swimming)MedalsRanked 5th Gold 34 Silver 33 Bronze 49 Total 116 ASEAN Para Games appearances (overview) 2001 2003 2005 2008 2009 2011 2013 2015 2017 2022 2023 The Philippines competed at the 2023 ASEAN Para Games in Phnom Penh, Cambodia which ran from 3 to 9 June 2023. The delegation led by chef de ...

American basketball player (born 1984) Carmelo AnthonyAnthony with the Los Angeles Lakers in 2022Personal informationBorn (1984-05-29) May 29, 1984 (age 39)New York City, New York, U.S.Listed height6 ft 7 in (2.01 m)Listed weight238 lb (108 kg)Career informationHigh school Towson Catholic(Towson, Maryland) Oak Hill Academy(Mouth of Wilson, Virginia) CollegeSyracuse (2002–2003)NBA draft2003: 1st round, 3rd overall pickSelected by the Denver NuggetsPlaying career...

City in Westchester County, New York New Rochelle redirects here. For other uses of Rochelle, see Rochelle. New Ro redirects here. For the singer, see New Ro (singer). City in New York, United StatesNew Rochelle, New YorkCityNew Roc City and New Rochelle police station FlagSealLogoNickname: Queen City of the SoundMotto(s): Nunquam Retrorsum(Never Backward)Location within Westchester County and the state of New YorkInteractive map of New RochelleCoordinates: 40°54′31″N 73°46′...

Ethnic group Filipinos in EgyptTotal population4,178 (2006)LanguagesTagalog · English · Other languages of the Philippines · Egyptian ArabicRelated ethnic groupsOverseas Filipinos Filipinos in Egypt consist of migrant workers in a variety of sectors, as well as a smaller number of international students.[1] An estimated 2,300 reside in Egypt legally, while another 1,878 live there illegally.[2] Employment A large number of Filipinos in...

Osaka City Council 大阪市会Ōsaka-shikaiTypeTypeUnicameral HistoryFounded1889 (1889) (municipal mergers of the Meiji era (明治の大合併) [1]LeadershipPresident (gichō)Kazutaka Ohashi, Osaka Ishin since May 27, 2021 Vice-President (fuku-gichō)Teruaki Nishizaki, Komeito since May 27, 2021 StructurePolitical groupsMajority (64) Osaka Ishin(46) Komeito (18) Minority (17) Liberal Democratic Party (11) Indep...

Short story by Anton ChekhovA MalefactorShort story by Anton ChekhovThe 1941 illustration by KukryniksyOriginal titleЗлоумышленникTranslatorConstance GarnettCountryRussiaLanguageRussianPublicationPublished inPeterburgskaya GazetaPublication date7 August 1885Published in English1919 A Malefactor (Russian: Злоумышленник, romanized: Zloumyshlennik) is an 1885 short story by Anton Chekhov.[1] Publication A Malefactor was first published in the 7 Aug...

1910s French light aircraft 1910 Monoplane Deperdussin monoplane belonging to the Shuttleworth Collection. Role Sports aircraftType of aircraft National origin France Manufacturer Aéroplanes Deperdussin Designer Louis Béchereau First flight 1910 The 1910 Deperdussin monoplane was the first aircraft to be built in significant quantities by Aéroplanes Deperdussin. The type was produced in a number of variants which were flown successfully in air races and gained several records during 1911, ...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 尚泰王 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2014年3月) 尚 泰王しょう たいおう 琉球国王・琉球藩王 晩年の...

日本 > 九州地方 > 福岡県 > 福岡市 > 中央区 > 南公園 南公園Minami Park 南公園(無料公園)分類 総合公園[1]所在地 日本福岡市中央区平尾、平尾浄水町、桜坂、谷、南公園(町丁)、小笹、御所ケ谷及び輝国[2]座標 北緯33度34分21.28秒 東経130度23分20.1秒 / 北緯33.5725778度 東経130.388917度 / 33.5725778; 130.388917座標: 北緯33�...

Private polytechnic in Nigeria Kings Polytechnic, Ubiaja Kings Polytechnic Kings Polytechnic is a private polytechnic in Ubiaja, Nigeria.[1][2][3] History It is an offspring of the new Era Institute of Technology, Ubiaja, which was established in 2005. The desire for the change from an institute to a polytechnic was a result of the foresight of the proprietor, Chief Sir Francis Anegbode Ijewere, a retired chief of banking operations of the Central Bank of Nigeria. He s...