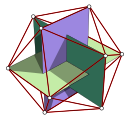
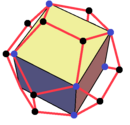
Sòlid platònic
|
Read other articles:

Collonge-Bellerive Lambang kebesaranNegaraSwissKantonGenevaDistrikn.a.Pemerintahan • WalikotaMaireFrancine de PlantaLuas[1] • Total6,12 km2 (2,36 sq mi)Ketinggian426 m (1,398 ft)Populasi (Kesalahan: waktu tidak sah.[2]) • Total7,578 • Kepadatan1,200/km2 (3,200/sq mi)Kode pos1245Kode area telepon6616Dikelilingi olehBellevue, Choulex, Cologny, Corsier, Meinier, Vandœuvres, VersoixSitus webwww.col...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Politerowongan – berita · surat kabar �...

Untuk senator negara bagian Oregon, lihat Lew Wallace (1889-1960). Lew Wallace Gubernur Teritorial New Mexico ke-11Masa jabatan1878–1881 PendahuluSamuel Beach AxtellPenggantiLionel Allen SheldonMenteri Amerika Serikat untuk Kekaisaran UtsmaniyahMasa jabatan1881–1885 PendahuluJames LongstreetPenggantiSamuel S. Cox Informasi pribadiLahirLewis Wallace10 April 1827 (1827-04-10)Brookville, IndianaMeninggalNot recognized as a date. Years must have 4 digits (use leading zeros for years <...

Universitas Sains dan Teknologi Tiongkok中国科学技术大学Moto红专并进,理实交融Moto dalam bahasa InggrisMenjadi bertanggung jawab dan profesional, mengintegrasikan teori dengan praktekJenisUniversitas negeriDidirikan1958PresidenBao XinheStaf akademik547Jumlah mahasiswa15.500Sarjana7.400Magister8.100LokasiHefei, Anhui, TiongkokKampusUrbanAfiliasiAEARU, APRU, Liga 9 UniversitasSitus webwww.ustc.edu.cn Universitas Sains dan Teknologi Tiongkok Gerbang Utara Lama Kampus Timur ...

Cyclamen sp. Dracaena sanderiana Tanaman dalam ruangan adalah tanaman yang ditanam di dalam ruangan umumnya di dalam kantor dan rumah. Tujuan ditanamnya tumbuhan di dalam ruangan adalah untuk dekorasi dan kesehatan (fisik maupun psikologis). Tanaman dalam ruangan memiliki kebutuhan hidup yang sama dengan tanaman di luar ruangan. Efek terhadap kualitas udara Tanaman dalam ruangan dan ekosistem yang menyertainya (termasuk fauna tanah) meningkatkan kualitas udara dalam ruangan dengan menyerap se...

Japanese samurai (1828–1877) who led the Satsuma Rebellion In this Japanese name, the surname is Saigō. This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2018) (Learn how and when to remove this template message) Saigō TakamoriA portrait of Takamori by Ishikawa ShizumasaNative name西郷 隆盛Birth nameSaigō KokichiOther name(s)Saigō NanshūSaig...

KelimaAlbum studio karya KLa ProjectDirilis2 November 1995GenrePopLabelPro SoundKronologi KLa Project Ungu(1994)Ungu1994 Kelima(1995) KLakustik(1996)KLakustik1996 Kelima (umumnya dikenal sebagai V) adalah album kelima KLa Project. Album ini dirilis tahun 1995 dengan mengusung lagu andalan Romansa. Di album ini, Wong Aksan (drummer Potret - eks drummer Dewa 19) dan Rere (drummer Grass Rock) membantu pembuatan album ini sebagai additional drummer. Daftar lagu Side A Romansa Terkenang Bahagi...

Artikel ini memerlukan pemutakhiran informasi. Harap perbarui artikel dengan menambahkan informasi terbaru yang tersedia. Logo resmi JFFF Jakarta Fashion & Food Festival (JFFF) JFFF merupakan sebuah festival tahunan persembahan Pemerintah Provinsi DKI Jakarta melalui Dinas Pariwisata dan Kebudayaan DKI Jakarta bekerja sama dengan PT Summarecon Agung Tbk., dan didukung oleh Kementerian Pariwisata dan Ekonomi Kreatif RI serta Kementerian Perdagangan RI. Sebuah keinginan terbesar dari hadirn...

Artikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa Inggris. Jika halaman ini ditujukan untuk komunitas bahasa Inggris, halaman itu harus dikontribusikan ke Wikipedia bahasa Inggris. Lihat daftar bahasa Wikipedia. Artikel yang tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak men...

Fakultas TeknikUniversitas Sam RatulangiJenisPerguruan Tinggi NegeriDidirikan1 September 1964 DekanProf. Dr. Ir. Fabian J Manoppo, M.Agr[1]LokasiManado, Sulawesi Utara, IndonesiaKampusUrbanAlamatFakultas Teknik, Jln. Kampus Unsrat, KleakWarnaBiru gelap Nama julukanFT-UNSRAT, FATEK-UNSRATSitus webhttp://fatek.unsrat.ac.id/ Fakultas Teknik Universitas Sam Ratulangi disingkat FT-UNSRAT atau FATEK-UNSRAT Merupakan salah satu Fakultas Dibawah naungan Universitas Sam Ratulangi Manado y...
此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Sports competition topic Basketball is the regular Asian Games sport since the first edition in Delhi 1951. The Asian Games tournaments were the de facto Asian championships until the Asian Basketball Confederation Championship was founded in 1960. Men's tournaments Summaries Year Host Final Third-place game Gold medalists Score Silver medalists Bronze medalists Score Fourth place Number teams 1951 Details New Delhi Philippines No playoffs Japan Iran No playoffs India 5 1954 Details Manila Ph...

† Стеллерова корова Муляж стеллеровой коровы в Лондонском музее естествознания Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстно�...

English football referee Scott Duncan Duncan refereeing in 2014Born Newcastle upon Tyne, EnglandDomesticYears League Role2008–2012 Football Conference Referee2010–2012 The Football League Assistant referee2012–2020 The Football League Referee Scott Duncan is an English former association football referee who officiated in the Football League. He first refereed in the Football Conference in 2008, and became an assistant referee in the Football League two years later. Duncan began referee...

Cinema of Hong Kong 1909–1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 19841985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 19941995 1996 1997 1998 1999 2000s 2000 2001 2002 2003 20042005 2006 2007 2008 2009 2010s 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020s 2020 2021 2022 2023 2024 vte This article lists feature-length Hong Kong...

Anglo-Welsh lawyer and statesman (1828–1911) The Right HonourableThe Lord James of HerefordGCVO PC KCLord James of Hereford, by Bassano, 1882Solicitor-GeneralIn office26 September 1873 – 20 November 1873MonarchVictoriaPrime MinisterWilliam Ewart GladstonePreceded bySir George JesselSucceeded bySir William Vernon HarcourtAttorney-GeneralIn office20 November 1873 – 17 February 1874MonarchVictoriaPrime MinisterWilliam Ewart GladstonePreceded bySir John ColeridgeSu...

n.SSignInformasi latar belakangAsalSeoul, Korea SelatanGenreK-popTahun aktif2023 (2023)–sekarangLabeln.CH EntertaintmentAnggota Kazuta Hyun Eddie Doha Junhyeok Sungyun Robin Hanjun Laurence Huiwon n.SSign adalah sebuah grup vokal laki-laki Korea Selatan yang berada di bawah naungan n.CH Entertainment. Grup tersebut debut pada tahun 2023 dan dibentuk melalui acara survival Stars Awakening. Pada awalnya, n.SSign dibentuk sebagai grup proyek dan kemudian diputuskan menjadi ...

För den gamla Olympiastadion, se Tokyos Olympiastadion (1958). Tokyos Olympiastadion Officiellt namn新国立競技場Placering10-2 Kasumigaoka-machi, Shinjuku-ku, TokyoNärmaste hållplatsKokuritsu-Kyōgijō station (Ōedo-linjen)Sendagaya station & Shinanomachi station (Chūō-Sōbu-linjen)Kapacitet68 000Byggkostnad¥149 miljarderArkitektKengo KumaEntreprenörTaisei Corporation Större evenemangOlympiska sommarspelen 2020Paralympiska sommarspelen 2020Datu...
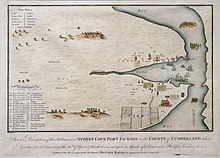
シドニー・オペラハウスとシドニー・ハーバーブリッジが飾るポート・ジャクソン湾。 フランシス・フォウクス(Francis Fowkes)による描写、1788年 大日本帝国軍特殊潜航艇によるシドニー港攻撃、1942年6月1日この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方�...

Collection of Gnostic and Christian texts Codex II, one of the most prominent Gnostic writings found in the Nag Hammadi library, which contains the end of the Gospel of Thomas and the beginning of the Apocryphon of John. Part of a series onGnosticism Gnostic concepts Adam kasia Adam pagria Aeon Anima mundi Archon Barbelo Demiurge Five Seals Gnosis Kenoma Luminary Manda Monad Ogdoad Pleroma Sophia Uthra World of Light World of Darkness Yaldabaoth Gnostic sects and founders List of Gnost...