Criteri de l'arrel
|
Read other articles:

Street in Berlin, Germany For the U-Bahn station of the same name, see Mohrenstraße (Berlin U-Bahn). MohrenstraßeView of Mohrenstraße, facing eastNative nameMohrenstraße (German)Length900 m (3,000 ft)LocationBerlin-MitteConstructionInaugurationMay 1707 You can help expand this article with text translated from the corresponding article in German. (August 2020) Click [show] for important translation instructions. View a machine-translated version of the German article. ...

خواجة ناظم الدين (بالبنغالية: খাজা নাজিমুদ্দিন) مناصب الحاكم العام لباكستان (2 ) في المنصب14 سبتمبر 1948 – 17 أكتوبر 1951 محمد علي جناح مالك غلام محمد رئيس وزراء باكستان في المنصب17 أكتوبر 1951 – 17 أبريل 1953 لياقت علي خان محمد علي بوغرا ...

Jennette McCurdyAlbum studio karya Jennette McCurdyDirilis05 Juni 2012 (2012-06-05)GenreCountryDurasi34:40LabelCapitol NashvilleProduserPaul WorleyJay DeMarcusKronologi Jennette McCurdy Jennette McCurdy (EP)(2012)Jennette McCurdy (EP)2012 Jennette McCurdy(2012) Singel dalam album Jennette McCurdy Generation LoveDirilis: April 25, 2011 Jennette McCurdy adalah sebuah album studio pertama dari penyanyi-penulis lagu Amerika Serikat, Jennette McCurdy. album ini dirilis pada 5 Juni 2012 vi...

American academic, homeopathic physician, and politician Royal Copeland redirects here. For another person, see Royal Copeland (Canadian football). Senator Copeland redirects here. For other uses, see Senator Copeland (disambiguation). Royal S. CopelandCopeland in 1923United States Senatorfrom New YorkIn officeMarch 4, 1923 – June 17, 1938Preceded byWilliam M. CalderSucceeded byJames M. MeadMayor of Ann Arbor, MichiganIn office1901–1903Preceded byGottlob LuickSucceeded byArthur B...

Letak Laval di Quebec Laval merupakan sebuah kota di Kanada. Kota ini letaknya di bagian selatan. Tepatnya di Provinsi Quebec. Pada tahun 2011, kota ini memiliki jumlah penduduk sebesar 401.553 jiwa dan memiliki luas wilayah 247,09 km². Kota ini memiliki angka kepadatan penduduk 1.625 jiwa/km². Logo Saint-Eustache, Boisbriand, Rosemère Lorraine, Bois-des-Filion Terrebonne Deux-Montagnes Barat Laval Timur Montreal Montreal Montreal Pranala luar Situs resmi Wikimedia Commo...

This article is about Indo-Greek kings. For the airplane, see Grob Strato 2C. Indo-Greek king Strato IISaka imitation of Strato IIIndo-Greek kingReign25 BCE – 10 CEPredecessorMenander II (dynastically)SuccessorStrato IIIDied10 CEMathuraReligionGreco-Buddhism Coin of Strato II.Obv: Bust of Strato II. Greek legend: BASILEOS SOTEROS STRATONOS Of King Strato the Savior.Rev: Athena holding a thunderbolt. Kharoshthi legend: MAHARAJASA TRATARASA STRATASA King Strato the Saviour. Strato II Soter (A...

Artikel ini bukan mengenai Iwa K, seorang rapper Indonesia Iwa Koesoemasoemantri Menteri Pertahanan Indonesia Ke-7Masa jabatan30 Juli 1953 – 12 Agustus 1955PresidenSoekarnoPerdana MenteriAli SastroamidjojoPendahuluWilopoPenggantiBurhanuddin HarahapMenteri Sosial Indonesia Ke-1Masa jabatan19 Agustus 1945 – 14 November 1945PresidenSoekarnoPendahuluTidak ada,Jabatan baruPenggantiA.D. Tjokronegoro Informasi pribadiLahir(1899-05-31)31 Mei 1899Ciamis, Hindia BelandaMen...

For other uses, see Fort Hamilton Parkway (disambiguation). New York City Subway station in Brooklyn New York City Subway station in Brooklyn, New York Fort Hamilton Parkway New York City Subway station (rapid transit)View from northbound platformStation statisticsAddressFort Hamilton Parkway & 62nd StreetBrooklyn, NYBoroughBrooklynLocaleBorough ParkCoordinates40°37′55.56″N 74°0′23.49″W / 40.6321000°N 74.0065250°W / 40.6321000; -74.0065250Di...

此條目可参照外語維基百科相應條目来扩充。若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 Osagyefo克瓦米·恩克鲁玛第三届非洲联盟主席任期1965年10月21日—1966年2月24日前任贾迈勒·阿卜杜-纳赛尔继任约瑟夫·亚瑟·�...
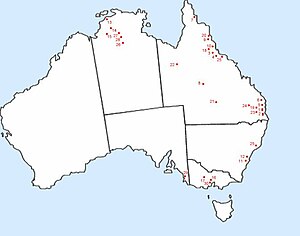
Airfields of the United States Army Air Forcein Australia Part of World War IIDate1942–1945LocationAustraliaResult Allied victory over the Empire of Japan (1945) Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) During World War II, the United States Army Air Forces established a series of airfields in Australia for the collective defense of the country, as well as for conducting offensive o...

A summary of anti-vaccine sentiment in the chiropractic profession This article is part of a series onAlternative medicine General information Alternative medicine History Terminology Alternative veterinary medicine Quackery (health fraud) Rise of modern medicine Pseudoscience Antiscience Skepticism Scientific Therapeutic nihilism Fringe medicine and science Acupressure Acupuncture Alkaline diet Anthroposophic medicine Apitherapy Applied kinesiology Aromatherapy Association for Research and E...

Language spoken by a minority of the population of a territory This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2010) (Learn how and when to remove this message) A minority language is a language spoken by a minority of the population of a territory. Such people are termed linguistic minorities or language minorities. With a total number of 196 sovereign ...

Drinking game This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dizzy bat – news · newspapers · books · scholar · JSTOR (December 2013) (Learn how and when to remove this message) A commercially available dizzy bat Dizzy bat (also known as Louisville chugger, D-bat, and The Spins) is a drinking game in which t...

Euclid Организация ESA Главные подрядчики Thales Alenia Space, Airbus Defence and Space[1] Волновой диапазон 550—900 нм (видимое) 920—2000 нм (инфракрасное) COSPAR ID 2023-092A NSSDCA ID 2023-092A SCN 57209 Местонахождение точка Лагранжа L2 системы Солнце — Земля (план)[1] Тип орбиты гало-орбита[6] Дата запуск...

UK Independence Party politician (born 1944) Roger KnapmanLeader of the UK Independence PartyIn office5 October 2002 – 27 September 2006DeputyMike NattrassChairmanDavid LottPetrina HoldsworthDavid Campbell BannermanPreceded byJeffrey TitfordSucceeded byNigel FarageLord Commissioner of the TreasuryIn office23 July 1996 – 1 May 1997Prime MinisterJohn MajorPreceded bySimon BurnsSucceeded byBob AinsworthMember of the European Parliament for South West England & Gibraltar...

Isla de Cebú Ubicación geográficaRegión FilipinasArchipiélago BisayasCoordenadas 10°21′00″N 123°41′00″E / 10.35, 123.68333333333Ubicación administrativaPaís FilipinasDivisión CebúSubdivisión CebúRegión Bisayas CentralesCaracterísticas generalesSuperficie 4422Punto más alto ()PoblaciónCapital CebúPoblación 4 632 359 hab. (1 de agosto de 2015)Gentilicio cebuano [editar datos en Wikidata] La isla de Cebú, llamada La...

この項目では、実在の戦車について説明しています。アニメ『機動戦士ガンダム』シリーズに登場する架空の戦車については「61式戦車 (ガンダムシリーズ)」をご覧ください。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 61式戦車 �...

Guillermo II de Alemania Fotografiado por T. H. Voigt, c. 1902Emperador de Alemania 15 de junio de 1888-9 de noviembre de 1918(30 años y 147 días)Predecesor Federico IIISucesor Friedrich Ebert(como Reichspräsident)Rey de Prusia 15 de junio de 1888-9 de noviembre de 1918(30 años y 147 días)Predecesor Federico IIISucesor Friedrich Ebert(como Ministro-presidente de Prusia)Información personalNombre completo Federico Guillermo Víctor AlbertoTratamiento Su Majestad...

Region of the Russian Empire where Jewish residents were allowed to reside This article is about the Pale in Imperial Russia. For other places referred to as pale, see Pale (disambiguation). Pale of SettlementЧерта осѣдлости1791–1915Pale of Settlement map, showing the percentage of the Jewish population in 1884Historical era124 years: From the late 18th to early 20th centuries• Established 1791• Disestablished 1915 Today part of7 countries: Belarus, Lithuania, Mo...

Theory that all societal relationships are based on economic relationships This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article is missing information about how Marx and Engles applied historical materialism in concrete cases and whether this makes the theory amount to a determinism. Please expand the article to include this information. Further details may exist on the talk page. (June 20...
![{\displaystyle \limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a45c76ebf0a8f41d32e50838cf0b682850536b7c)



![{\displaystyle C=\lim _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/039df6d05beebc6b2bb5b473fef1cf11bc7487ef)



![{\displaystyle 1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ed96c19c6b5a78f5da594254b249565e3bd4bea)
![{\displaystyle {\sqrt[{n}]{a_{n}}}<k<1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d12f1cc5a40a2513534b80e8ec650eeed71a97b)



![{\displaystyle {\sqrt[{n}]{|a_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36ec6e0a6106eb370acdcb9ee890fa2602d103f0)
![{\displaystyle {\sqrt[{n}]{|a_{n}|}}>1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c535ba7887a7dcf0f6ce3412cd6e80e94ccc741)
![{\displaystyle {\sqrt[{n}]{|a_{n}|}}={\sqrt[{n}]{|c_{n}(z-p)^{n}|}}<1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/146709dd34f62c2e43148958f74137a52f60f735)
![{\displaystyle {\sqrt[{n}]{|c_{n}|}}\cdot |z-p|<1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1768dd66e43115fcdaa24f6780c55b6560cce050)
![{\displaystyle |z-p|<1/{\sqrt[{n}]{|c_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c6c5293853a4885d4fc145b610faf3da2bae938)
![{\displaystyle |z-p|<1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8412b175cc4f9f3d2182c7812be4fc6dd574043)
![{\displaystyle R\leq 1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/311cd74e487ff6fec0311250c25c27e57cffd333)
![{\displaystyle {\sqrt[{n}]{|a_{n}|}}={\sqrt[{n}]{|c_{n}(z-p)^{n}|}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2c8e6658ec2f62ab2c6e1164010159d6d4d89c1)
![{\displaystyle R=1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98d577afed3a2905c4e3d3f7f3522b21f2d2d90b)