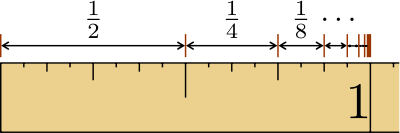
Sèrie geomètrica
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Agustus 2012. King Air CharterPenghubungBandar Udara LanseriaArmada3Kantor pusatLanseria, Afrika SelatanSitus webhttp://www.kingair.co.za/ King Air Charter adalah maskapai penerbangan sewaan yang berbasis di Lanseria, Afrika Selatan. Armada Armada King Air Charter t...

EnninPatung Ennin.Lahir793 atau 794 MasehiMeninggal864 MasehiPekerjaanbiksu, filsuf, sarjana, penjelajah, dan pendeta Ennin (圓仁 atau 円仁code: ja is deprecated , 793 Masehi [1] atau 794 – 864), juga dikenal di Jepang dengan nama anumerta-nya, Jikaku Daishi (慈覺大師), adalah seorang pendeta dari aliran Tendai. Kelahiran dan asal mula Bagian dari sebuah serial tentangAgama Buddha di Jepang Aliran Jōjitsu Hosso Sanron Kegon Ritsu Kusha Tendai Shingon Tanah Murni Zen Nichir...

لمعانٍ أخرى، طالع لاغوس (توضيح). لاغوس تقسيم إداري البلد اليونان [1] التقسيم الأعلى بلدية ديموتيقة [لغات أخرى] إحداثيات 41°27′05″N 26°27′43″E / 41.451297°N 26.461883°E / 41.451297; 26.461883 السكان التعداد السكاني 620 (إحصاء السكان) (2011)451 (resident population of Greece) (202...

L'escatologia islamica riguarda quegli aspetti (dogmatici e non) che nel sistema dei valori e delle credenze musulmane si preoccupano di indicare quale sia il destino del genere umano dopo la morte e la risurrezione voluta da Allah nel Giorno del Giudizio. L'assetto escatologico è, tutto sommato, abbastanza semplice e, nei suoi aspetti dogmatici tratta in successione il tormento della tomba, la Bilancia, il Ponte e il Bacino. Secondo l'escatologia islamica, sacrilegi sul Monte del Tempio...

UGM-96 Trident I, atau Trident C4 adalah sebuah peluru kendali / rudal balistik Amerika yang diluncurkan Submarine, dibangun oleh Lockheed Martin Space Systems di Sunnyvale, California. Pertama digunakan pada tahun 1979, Trident I menggantikan rudal Poseidon. Ini sudah pensiun pada tahun 2005, [2] yang telah digantikan oleh Trident II. Trident I adalah tiga tahap, rudal berbahan bakar padat. Referensi Wikimedia Commons memiliki media mengenai Trident missile. lbsSistem penggolongan peluru ke...

The Om symbol in Devanagari Hinduism is a minority religion in Hungary. According to the 2022 census, there were 3,307 Hindus in Hungary (comprising 0.03% of the population).[1] International Society for Krishna Consciousness The International Society for Krishna Consciousness (ISKCON) runs the Bhaktivedanta Theological College in Hungary. The Hungarian government donated a building for the Bhaktivedanta Theological College. Krishna devotees first appeared in Hungary at the end of th...

Pasquale Fornara Nazionalità Italia Ciclismo Specialità Strada Termine carriera 1961 - ciclista Carriera Squadre di club 1946-1947S.C. Crennese1948Individuale1949-1951 Legnano1951-1953 Cilo1952 Bianchi1952-1954 Bottecchia1955 Bottecchia1955Leo-Chlorodont1956 Saint-Raphaël1956 Allegro1956-1957 Arbos1956-1958 Cilo1958 Ignis1959-1960 Emi1960 Mondia1961 Vov Nazionale 1953-1956 Italia Carriera da allenatore 1965 Cynar ...

Unproven alternative medicine This article is part of a series onAlternative medicine General information Alternative medicine History Terminology Alternative veterinary medicine Quackery (health fraud) Rise of modern medicine Pseudoscience Antiscience Skepticism Scientific Therapeutic nihilism Fringe medicine and science Acupressure Acupuncture Alkaline diet Anthroposophic medicine Apitherapy Applied kinesiology Aromatherapy Association for Research and Enlightenment Auriculotherapy Bates me...

American discus thrower Shelbi VaughanPersonal informationFull nameShelbi JoDae VaughanNationalityAmericanBorn (1994-08-24) August 24, 1994 (age 29)Weatherford, Texas, U.S.[1]Height6 ft 2 in (1.88 m)[2]SportSportTrack and fieldEventDiscus throwCollege teamTexas A&M UniversityAchievements and titlesPersonal best(s)Discus throw 64.52 m (211 ft 8 in) Weight throw 18.73 m (61 ft 5+1⁄4 in) Hammer throw 54.11 m (1...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

1770s–1880s Jewish intellectual movement Maskil redirects here. For the Hebrew literary term heading some psalms, see Psalms § Themes and execution. Top row, proto-Maskilim: Raphael Levi Hannover • Solomon Dubno • Tobias Cohn • Marcus Elieser Bloch 2nd row, Berlin Haskalah: Salomon Jacob Cohen • David Friedländer • Naphtali Hirz Wessely • Moses Mendelssohn3rd row, Austria and Galicia: Judah Löb Mieses • Solomon Judah Loeb Rapoport • Joseph Perl • Baruch Jeitteles B...

The harbour and jetty at Lundy The coins of Lundy are unofficial issues of currency from the island of Lundy, in the Bristol Channel off the west coast of England.[1] Two bronze coins, the half puffin and one puffin, were issued with a 1929 date and featured a portrait of Martin Coles Harman, who owned the island and was responsible for the issue. The coins were struck again with slightly modified designs and updated dates in 1965, 1977, and 2011, as commemorative or fantasy tokens no...

Business that makes and sells beer See also: Winery Kettles in a modern Trappist brewery A brewery or brewing company is a business that makes and sells beer. The place at which beer is commercially made is either called a brewery or a beerhouse, where distinct sets of brewing equipment are called plant.[1] The commercial brewing of beer has taken place since at least 2500 BC;[2] in ancient Mesopotamia, brewers derived social sanction and divine protection from the goddess Nin...

Type of heavy cavalry that wore a cuirass French cuirassier (1809) Cuirassiers (/ˌkwɪrəˈsɪər/; from French cuirassier[1] [kɥiʁasje]) were cavalry equipped with a cuirass, sword, and pistols. Cuirassiers first appeared in mid-to-late 16th century Europe as a result of armoured cavalry, such as men-at-arms and demi-lancers discarding their lances and adopting pistols as their primary weapon.[2] In the later part of the 17th century, the cuirassier lost h...

1966 television film by Terence Young The Poppy Is Also a FlowerWritten byJo EisingerIan Fleming (story)Directed byTerence YoungStarringE. G. MarshallTrevor HowardYul BrynnerEli WallachAngie DickinsonNarrated byGrace KellyMusic byGeorges AuricOriginal languageEnglishProductionProducersEuan LloydCinematographyHenri AlekanRunning time80 minutesOriginal releaseNetworkABCRelease1966 (1966) The Poppy Is Also a Flower is a 1966 American-French-Austrian made-for-television spy and anti-drug fil...

Pour les articles homonymes, voir Lunel (homonymie) et Viel. Lunel-Viel Hôtel de ville Blason Administration Pays France Région Occitanie Département Hérault Arrondissement Montpellier Intercommunalité Communauté de communes du Pays de Lunel Maire Mandat Fabrice Fenoy 2020-2026 Code postal 34400 Code commune 34146 Démographie Gentilé Lunelviellois Populationmunicipale 4 488 hab. (2021 ) Densité 375 hab./km2 Géographie Coordonnées 43° 40′ 44″ nord...

Surgical procedure on the heart Atrial septostomyBalloon atrial septostomyICD-9-CM35.41[edit on Wikidata] Atrial septostomy is a surgical procedure in which a small hole is created between the upper two chambers of the heart, the atria. This procedure is primarily used to palliate dextro-Transposition of the great arteries or d-TGA (often imprecisely called transposition of the great arteries), a life-threatening cyanotic congenital heart defect seen in infants. It is performed prior to a...

1990 British filmTruly, Madly, DeeplyReproduction posterDirected byAnthony MinghellaWritten byAnthony MinghellaProduced byRobert CooperStarring Juliet Stevenson Alan Rickman Bill Paterson Michael Maloney CinematographyRemi AdefarasinEdited byJohn StothartMusic byBarrington PheloungProductioncompaniesBBC FilmsLionheartWinstonDistributed byThe Samuel Goldwyn CompanyRelease dates 10 November 1990 (1990-11-10) (BFI London Film Festival) 3 May 1991 (1991-05-03)&#...

1999 film directed by Takao Okawara This article is about the 1999 film. For the unrelated novel, see Godzilla (Marc Cerasini series) § Godzilla 2000. Godzilla 2000: MillenniumTheatrical release posterJapanese nameKatakanaゴジラ2000 ミレニアムTranscriptionsRevised HepburnGojira Nisen: Mireniamu Directed byTakao OkawaraWritten byHiroshi Kashiwabara [ja]Wataru MimuraProduced byShogo TomiyamaStarring Takehiro Murata [ja] Hiroshi Abe Naomi Nishida Mayu Suzu...

GP della Malesia 2011 795º GP della storia del Motomondiale17ª prova su 18 del 2011 Data 23 ottobre 2011 Nome ufficiale Shell Advance Malaysian Motorcycle Grand Prix Luogo Circuito di Sepang Percorso 5,548 km Clima Soleggiato Risultati MotoGP Pole position Giro veloce Daniel Pedrosa Honda in 2:01.462 Moto2 33º GP nella storia della classe Distanza 17 giri, totale 94,316 km Pole position Giro veloce Thomas Lüthi Stefan Bradl Suter in 2:07.512 Kalex in 2:08.220 (nel giro 4 di 17) Pod...