Cúpulorotonda pentagonal giroallargada

Cúpulorotonda pentagonal giroallargada
Elements

Model 3D
Tipus	Sòlid de Johnson
Forma de les cares	Triangles equilàters quadrats i pentàgons
Cares per vèrtex	4 i 5
Vèrtexs per cara	3, 4 i 5
Simetria	C₅
Dual	-
Propietats	Convex

Cares	47
Arestes	80
Vèrtexs	35

Característica	2
Més informació
MathWorld	GyroelongatedPentagonalCupolarotunda

En geometria, la cúpulorotonda pentagonal giroallargada es pot construir giroallargant una cúpulorotonda pentagonal J₃₂ o J₃₃ inserint un antiprisma decagonal entre les dues meitats. És un dels noranta-dos sòlids de Johnson (J₄₇). Té simetria C₅.

La cúpulorotonda pentagonal giroallargada és un dels cinc sòlids de Johnson que són quirals, això vol dir que tenen una forma de "mà esquerra" i una altra de "mà dreta". A la il·lustració de la dreta, cada cara pentagonal de la meitat de baix de la figura, excepte la cara pentagonal de baix de tot, està connectada a través de dues cares triangulars a una cara quadrada de damunt i a l'esquerra seu. A la figura de quiralitat oposada (la imatge especular de la que es presenta a la figura), aquests pentàgons de baix estarien connectats a una cara quadrada a damunt i a la dreta seu. Les dues formes quirals de J₄₇ no es consideren sòlids de Johnson diferents.

Els 92 sòlids de Johnson van ser descrits 1966 per Norman Johnson i els va numerar. No va demostrar que no n'existia més que 92, però va conjecturar que no n'hi havia d'altres. Victor Zalgaller el 1969 va demostrar que la llista de Johnson era completa. S'utilitzen els noms i l'ordre donats per Johnson, i se'ls nota J_xx on xx és el nombre donat per Johnson.

Desenvolupament pla

Referències

Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Conté l'enumeració original dels 92 sòlids i la conjectura que no n'hi ha d'altres.
Victor A. Zalgaller, "Convex Polyhedra with Regular Faces", 1969 : primera demostració d'aquesta conjectura.
Eric W. Weisstein. Johnson Solid : cada sòlid amb el seu desenvolupament

Vegeu també

Enllaços externs

Weistein, Eric W., Gyroelongated Pentagonal Cupolarotunda cúpulorotonda pentagonal giroallargada a MathWorld. (anglès)
Weistein, Eric W., Johnson solid Sòlids de Johnson a MathWorld. (anglès)

Read other articles:

Arondisemen Haguenau

Arondisemen Haguenau Administrasi Negara Prancis Region Alsace Departemen Bas-Rhin Kanton 3 Komune 56 Sous-préfecture Haguenau Statistik Luas¹ 666 km² Populasi - 1999 120,445 - Kepadatan 181/km² Lokasi Lokasi Haguenau di Alsace ¹ Data Pendaftaran Tanah Prancis, tak termasuk danau, kolam, dan gletser lebih besar dari 1 km² (0.386 mi² atau 247 ekar) juga muara sungai. Arondisemen Haguenau merupakan sebuah arondisemen di Prancis, terletak di département Bas-Rhin, di ...

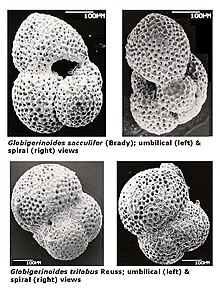
Globigerinida

2px solid red; error:colour</ includeonly> 2px solid red; error:colour</ includeonly> colspan=2 | GlobigerinidaRentang fosil: Jurassic - Recent colspan=2 | Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Rhizaria Filum: Foraminifera Ordo: Globigerinida colspan=2 | Superfamilies Globigerinacea Globorotaliacea Globotruncanacea Hantkeninacea Heterohelicacea Planomalinacea Rotaliporacea Globigerina adalah grup foraminifera yang ditemukan sebagai plankton maritim. Grup ini meliputi leb...

Bendera pribadi ratu Barbados

Bendera Pribadi Ratu Barbados Bendera Pribadi Ratu Barbados adalah bendera dari Ratu Elizabeth II dalam perannya sebagai Ratu dari Barbados. Bendera ini telah disetujui untuk digunakan pada 1970-an dan hanya digunakan oleh Ratu ketika dia berada di Barbados atau menghadiri sebuah acara di luar negeri dalam perannya sebagai kepala negara Barbados. Perwakilan Ratu, Gubernur-Jenderal Barbados memiliki bendera sendiri . Bendera ratu memiliki tiga bentuk: bendera terpusat terdiri dari pohon ara be...

العلاقات الإكوادورية السيشلية

العلاقات الإكوادورية السيشلية الإكوادور سيشل الإكوادور سيشل تعديل مصدري - تعديل العلاقات الإكوادورية السيشلية هي العلاقات الثنائية التي تجمع بين الإكوادور وسيشل.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه الم...

Westlaw

Online legal research service This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (October 2021) (Learn how and when to remove this template message) WestlawCompany typeSubsidiaryIndustryPublishingFounded1975; 49 years ago (1975)ProductsCase law, articles, publications, news, court documents, lawyer...

Sword and sorcery

Genre of fantasy fiction This article is about the subgenre. For other uses, see Swords & sorcery (disambiguation). Not to be confused with Sword and sandal, a genre of Italian costume adventure epic films Fantasy Media Anime Art Artists Authors Comics Films Podcasts Literature Magazines Manga Publishers Light novels Television Webcomics Genre studies Creatures History Early history Magic Magic item Magic system Magician Mythopoeia‎ Tropes Fantasy worlds Campaign settings Subgenres Bang...

Mitologi Batak

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Mitologi Batak – berita · surat kabar · buku · cendekiawan · JSTOR Artikel ini adalah bagian dari seriAgama asli Nusantara Sumatra Ugamo Malim • Pemena • Arat Sabulungan • Fanömba a...

Lingua olandese

OlandeseNederlandsParlato in Paesi Bassi Belgio (Fiandre e Regione di Bruxelles-Capitale) Suriname Aruba (lingua ufficiale assieme al papiamento) Curaçao (lingua ufficiale assieme al papiamento) Sint Maarten (lingua ufficiale assieme all'inglese) Francia (minoranza nazionale nelle Fiandre francesi) Germania (tra il confine con i Paesi Bassi e la regione della Ruhr) Indonesia LocutoriTotale29,5 milioni (Ethnologue, 2022) Classifica51 (2019) Altre ...

Collins Aerospace

Collins AerospaceJenisAnak perusahaanIndustriDirgantara dan IndustrialPendahuluGoodrich Corporation, Hamilton Sundstrand, Hamilton Standard, Sundstrand Corporation, dan Rockwell CollinsDidirikan2012 (UTAS) 2018 (Collins Aerospace)KantorpusatWest Palm Beach, Florida, Amerika SerikatProdukSistem Aktuasi, Aerostruktur, Sistem Manajemen Udara, Sistem listrik, Komponen Mesin, Sistem Kendali & Mesin, Interior, Sistem ISR, Peralatan Pendaratan, Sistem Baling-baling, Sensor & Sistem Terintegr...

Frederick Kerr

British actor (1858–1933) This article is about the actor. For the Kansas state senator, see Fred Kerr.For the Australian rugby union player, see Frederick Kerr (rugby union). Frederick KerrBornFrederick Grinham Keen(1858-10-11)11 October 1858London, UKDied3 May 1933(1933-05-03) (aged 74)London, UKResting placeGolders Green CrematoriumOccupationsActortheatrical managerYears active1882–1933SpouseLucy Dowson Frederick Kerr (born Frederick Grinham Keen, 11 October 1858 – 3 May 19...

Avro 504

1913 multi-role military aircraft family Avro 504 Role Trainer, Fighter, BomberType of aircraft Manufacturer Avro First flight 18 September 1913[1] Introduction 1913 Retired 1934 Primary users Royal Flying CorpsRoyal Naval Air Service Produced 1913–1932 Number built 11,303 including Japanese, Soviet and other foreign production[2] The Avro 504 was a First World War biplane aircraft made by the Avro aircraft company and under licence by others. Production during the war ...

Império Safárida

Império Safárida ← ← 861 — 1003 → → Império Safárida sob Iacube ibne Alaite Alçafar Região Ásia Central Planalto Iraniano Capital Zaranje Países atuais Afeganistão Irã Paquistão Quirguistão Tajiquistão Turcomenistão Usbequistão Línguas oficiais Árabe Persa Religião Islamismo sunita Moeda Dirrã Dinar Emir • 861–879 Iacube ibne Alaite Alçafar (primeiro) • 963–1002 Calafe ibne Amade (último) Período histórico Idade Média •&...

Karpal Singh

Yang Berhormat Dato' SriKarpal Singh Ketua Nasional Partai Aksi Demokratis ke-3Masa jabatan4 September 2004 – 29 Maret 2014PendahuluLim Kit SiangPenggantiTan Kok Wai (Acting)Anggota Parlemen Malaysiadapil Bukit GelugorMasa jabatan24 Maret 2004 – 17 April 2014PendahuluKonstituensi baruPenggantiRamkarpal SinghAnggota Parlemen Malaysiadapil JelutongMasa jabatan31 Juli 1978 – 29 November 1999PendahuluRasiah RajasingamPenggantiLee Kah Choon Informasi pribadiLahirKa...

John Joseph Adams

For American sports fan, see John Adams (drummer). American editor, critic, and publisher John Joseph AdamsBorn (1976-07-31) July 31, 1976 (age 47)OccupationEditor, journalist, essayistNationalityAmericanGenreScience fiction, FantasyWebsitewww.johnjosephadams.com John Joseph Adams (born July 31, 1976) is an American science fiction and fantasy editor, critic, and publisher. Career Editor Adams in 2009 Adams worked as Assistant Editor at The Magazine of Fantasy & Science Fiction from ...

Landratsamt Altenburger Land

Das Landratsamt Altenburger Land ist der Verwaltungssitz des Landkreises Altenburger Land im Osten Thüringens in der Skat- und Residenzstadt Altenburg. Vormals war es Sitz des Landratsamtes Altenburg (1900–1922), des Landkreises Altenburg (1922–1952) und des Kreises Altenburg (1952–1994). Das Hauptgebäude befindet sich in der Lindenaustraße 9. Inhaltsverzeichnis 1 Geschichte 2 Gestaltung 3 Ausstellungen 4 Verwaltungsgebäude 4.1 Weitere Einrichtungen 5 Weblinks Geschichte Landratsamt...

Stazione di Imamiya

Questa voce o sezione sull'argomento stazioni del Giappone non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Imamiyastazione ferroviaria今宮駅 LocalizzazioneStato Giappone LocalitàNishinari-ku, Ōsaka Coordinate34°39′15.04″N 135°29′34.95″E34°39′15.04″N, 135°29′34.95″E Linee JR West ■ Circolare Osaka ■ Linea Yamatoji StoriaS...

Città metropolitana di Palermo

Città metropolitana di Palermocittà metropolitana Città metropolitana di Palermo – VedutaPalazzo Comitini, sede istituzionale LocalizzazioneStato Italia Regione Sicilia AmministrazioneCapoluogo Palermo Sindaco metropolitanoRoberto Lagalla (UdC) dal 20-6-2022 Data di istituzione4 agosto 2015 TerritorioCoordinatedel capoluogo38°06′56″N 13°21′41″E38°06′56″N, 13°21′41″E (Città metropolitana di Palermo) Superficie5 009,28 km² Abitanti1 1...

Papa Milziade

Papa Milziade32º papa della Chiesa cattolicaElezionenovembre 310/giugno 311 Insediamento2 luglio 311 Fine pontificato10 gennaio 314 Predecessorepapa Eusebio Successorepapa Silvestro I NascitaNordafrica, ? MorteRoma, 10 gennaio 314 SepolturaCatacombe di San Callisto ma la tradizione vuole che i suoi resti siano conservati nella chiesa di San Silvestro in Capite. Manuale San Milziade Papa NascitaNordafrica, ? MorteRoma, 10 gennaio 314 Venerato daTutte le Chiese che a...

غلين إلدر

غلين إلدر الإحداثيات 39°29′59″N 98°18′27″W / 39.4997°N 98.3075°W / 39.4997; -98.3075 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ميتشل خصائص جغرافية المساحة 1.134836 كيلومتر مربع1.134839 كيلومتر مربع (1 أبريل 2010) ارتفاع 437 متر عدد السكا...

Success Park 'n' Ride

Bus station in Perth, Western Australia The topic of this article may not meet Wikipedia's notability guideline for geographic features. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Success Park 'n' Ride – news · newspa...