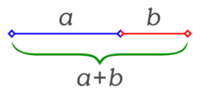
Златно сечение
|
Read other articles:

Potret Henri Lammens Henri Lammens (1 Juli 1862 – 23 April 1937) adalah seorang orientalis dan anggota Serikat Yesus asal Belgia. Ia menulis berbagai sejarah awal Islam dalam bahasa Prancis. Referensi Biography of Henri Lammens, by Stijn Knuts Pengawasan otoritas Umum Integrated Authority File (Jerman) ISNI 1 VIAF 1 WorldCat Perpustakaan nasional Norwegia Prancis (data) The ICCU id SBLV269685 is not valid. Amerika Serikat Australia Yunani Israel Belanda Polandia Swedia Vatikan...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Barrens film – news · newspapers · books · scholar · JSTOR (August 2016) (Learn how and when to remove this template message) 2012 American filmThe BarrensHome video release posterDirected byDarren Lynn BousmanScreenplay byDarren Lynn BousmanProduced b...

American politician David W. AlexanderBornJune 22, 1812IrelandDiedApril 29, 1886 (1886-04-30) (aged 73)Los Angeles, CaliforniaOccupationsSheriffSpouseAdelaida Johnson MellusChildren5RelativesGeorge C. Alexander (brother) David W. Alexander (June 22, 1812 – April 29, 1886) was an early California politician and pioneer in Los Angeles County, California. He was on the Board of Supervisors in 1853 and 1854, and in 1855 he was elected the third sheriff for the county. Biography Early ...

Questa voce sull'argomento guerra è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. La tattica militare è una delle cinque branche che compongono l'arte militare: strategia militare, arte operativa, tattica militare, logistica militare, organica militare (quest'ultima detta anche logistica del personale). Essa tratta dei metodi di impiego delle forze nel combattimento riferiti al livello tattico, che gi...

Progetto:Forme di vita - implementazione Classificazione APG IV.Il taxon oggetto di questa voce deve essere sottoposto a revisione tassonomica. Se vuoi contribuire all'aggiornamento vedi Progetto:Forme di vita/APG IV. Come leggere il tassoboxMiscanthus Giganteus Miscanthus Giganteus Classificazione scientifica Dominio Eukaryota Regno Plantae Sottoregno Magnoliophyta Superdivisione Spermatophyta Divisione Magnoliophyta Classe Liliopsida Ordine Poales Famiglia Poaceae Sottofamiglia Panicoideae...

Bucking BroadwayCuplikan filmSutradaraJohn FordProduserHarry CareyDitulis olehGeorge HivelyPemeranHarry CareyMolly MaloneSinematograferJohn W. BrownBen F. ReynoldsPerusahaanproduksiUniversal Film Manufacturing CompanyDistributorUniversal Film Manufacturing CompanyTanggal rilis24 Desember 1917Durasi53 menit (versi restorasi)NegaraAmerika SerikatBahasaBisu (intertitel Inggris) Bucking Broadway Bucking Broadway adalah sebuah film koboi bisu Amerika Serikat tahun 1917 garapan John Ford, diyakini ...

US nature reserve Big Lake National Wildlife RefugeIUCN category IV (habitat/species management area)Map of the United StatesLocationMississippi County, Arkansas, United StatesNearest cityManila, ArkansasCoordinates35°55′N 90°07′W / 35.917°N 90.117°W / 35.917; -90.117Area11,047 acres (44.71 km2) (2014)[1]Established1915Governing bodyU.S. Fish and Wildlife ServiceWebsiteBig Lake National Wildlife Refuge Big Lake National Wildlife Refu...

Magnus NormanMagnus Norman in 2013Kebangsaan SwediaTempat tinggalMonte Carlo, MonakoLahir30 Mei 1976 (umur 47)Filipstad, SwediaTinggi188 m (616 ft 10 in)Memulai pro1995Pensiun2004 (terakhir bermain pada September 2003)Tipe pemainTangan kanan (two-handed backhand)Total hadiah$4,537,247TunggalRekor (M–K)244–177Gelar12Peringkat tertinggiNo. 2 (12 Juni 2000)Hasil terbaik di Grand Slam (tunggal)Australia TerbukaSF (2000)Prancis TerbukaF (2000)Wimbledon3R (1997, 19...

Vehicle handling problem Diagram of a car undergoing fishtailing. Video of a car fishtailing or drifting on the street of Riia maantee in Tartu, Estonia (December 2021) Fishtailing is a vehicle handling problem which occurs when the rear wheels lose traction, resulting in oversteer. This can be caused by low-friction surfaces (sand, gravel, rain, snow, ice, etc.). Rear-drive vehicles with sufficient power can induce this loss of traction on any surface, which is called power-oversteer.[1&...

ملعب متروبوليتانو دي فتبول دي لارامعلومات عامةالمنطقة الإدارية باركيسيميتو البلد فنزويلا التشييد والافتتاحالافتتاح الرسمي 2007 الاستعمالالرياضة كرة القدم المستضيف ديبورتيفو لارا المالك لارا معلومات أخرىالطاقة الاستيعابية 40٬312 الموقع الجغرافيالإحداثيات 9°59′37″N 69°13...

Castello di BelcaroPortone di ingresso del castelloUbicazioneStato attuale Italia RegioneToscana CittàSiena IndirizzoStrada Terrensano e Belcaro, 32 Coordinate43°18′25.31″N 11°17′26.56″E43°18′25.31″N, 11°17′26.56″E Informazioni generaliTipoCastello medievale - villa Inizio costruzioneXII secolo VisitabilePrimo lunedì del mese[1] www.regione.toscana.it voci di architetture militari presenti su Wikipedia Modifica dati su Wikidata · Manuale Il castello di...

Cet article contient une liste des principales villes du Sri Lanka. Recensement de 2011 Sachant que pendant trois décennies, plusieurs provinces du Nord et de l'Est du Sri Lanka étaient dirigées par le groupe séparatiste LTTE, le gouvernement Sri lankais estime qu'entre 1981 et 2009, le nombre d'habitants des villes de ces Provinces a été faussé délibérément. Ainsi, le département des Statistiques du Ministère des Finances a ordonné un recensement de la population en 2009. Les r�...

دينيس أليبيك (بالرومانية: Denis Alibec) معلومات شخصية الاسم الكامل دينيس أليبيك الميلاد 5 يناير 1991 (33 سنة)[1] مانغالايا الطول 1.87 م (6 قدم 1 1⁄2 بوصة) مركز اللعب مهاجم الجنسية رومانيا الديانة مسيحية أرثوذكسية[2] معلومات النادي النادي الحالي ف...

Questa voce sull'argomento ciclisti svizzeri è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Jean-Marie GrezetNazionalità Svizzera Ciclismo SpecialitàStrada Termine carriera1987 CarrieraSquadre di club 1981-1982 Cilo-Aufina1983 Sem1984-1985 Skil1985-1986 Cilo-Aufina1987 Paini-Sidi Nazionale 1981-1985 Svizzera Modifica dati su Wikidata · Manuale Jean-Marie Grezet (Le Locle, 16 gennaio 1959) è un ex ciclista...

FREEDOM ジャンル SF OVA:FREEDOM 監督 森田修平 シリーズ構成 佐藤大、千葉克彦 脚本 佐藤大、千葉克彦、野村祐一 キャラクターデザイン 大友克洋、桟敷大祐、入江篤 メカニックデザイン 大友克洋、末武康光 音楽 池頼広 アニメーション制作 サンライズ 製作 FREEDOM製作委員会 発売日 2006年11月24日 発表期間 2006年11月17日 - 2008年5月16日 話数 全6+1話 その他 楽曲提供:宇多田�...

New York City Subway station in Brooklyn For the station formerly at Eastern Parkway & Snediker Avenue, see Eastern Parkway (BMT Fulton Street Line). New York City Subway station in Brooklyn, New York Eastern Parkway– Brooklyn Museum New York City Subway station (rapid transit)Manhattan-bound platformStation statisticsAddressWashington Avenue & Eastern ParkwayBrooklyn, New YorkBoroughBrooklynLocaleProspect HeightsCoordinates40°40′18″N 73°57′46�...

1992 Albanian parliamentary election ← 1991 22 March 1992 (1992-03-22) 1996 → All 140 seats in People's Assembly71 seats needed for a majority Party Leader Vote % Seats +/– PD Sali Berisha 57.61 92 +17 PS Fatos Nano 23.87 38 −131 PSD Skënder Gjinushi 4.06 7 New PR Sabri Godo 2.89 1 +1 PBDNJ Vasil Melo 2.69 2 −3 This lists parties that won seats. See the complete results below.Results by district Prime Minister before Prime Minister after Vilson...

Kraków VoivodeshipPalatinatus Cracoviensis Województwo KrakowskieVoivodeship of Poland1300–1795 Coat of arms Kraków Voivodeship in the Polish–Lithuanian Commonwealth in 1635.CapitalKrakówArea • 160610,000 km2 (3,900 sq mi)Population • 1606 320,000 History • Established 5 January 1300• First partition August 5, 1772• Third partition 24 October 1795 Political subdivisionscounties: 7 (as for 1662) Preceded by Succeeded by ...

American baseball player, coach, and manager For the minister and president of Columbia College Chicago, see George L. Scherger. Baseball player George SchergerScherger with the Nashville Sounds in 1979CoachBorn: (1920-11-10)November 10, 1920Dickinson, North Dakota, U.S.Died: October 13, 2011(2011-10-13) (aged 90)Charlotte, North Carolina, U.S.Batted: RightThrew: Right Teams Cincinnati Reds (1970–1978, 1983–1986) Career highlights and awards 2× World Series champion (1975, 1976) Geo...

Medieval region in current Belgium and France County of HainautComté de Hainaut (French)Graafschap Henegouwen (Dutch)c. 900/1190–1797 Flag Coat of arms StatusCountyCapitalMonsCommon languagesFrenchPicardLatin (religious, theological)Religion Roman CatholicismGovernmentFeudal lordshipCount of Hainaut • ?–898 Reginar I(first Reginar count)• 1071–98 Baldwin II• 1432–67 Philip the Good, Duke of Burgundy• 1477–82 Mary of Burgundy•&...