Пирамида
|
Read other articles:

Keuskupan NovalichesDiœcesis NovalichesinaDiyosesis ng Novaliches Diócesis de NovalichesKatolik Lambang Keuskupan NovalichesLokasiNegara FilipinaProvinsi gerejawiManilaStatistikLuas138 km2 (53 sq mi)Populasi- Total- Katolik(per 1 Mei 2012)2.545.3981,610,137 (63%%)Paroki70Sekolah9InformasiDenominasiKatolikGereja sui iurisGereja LatinRitusRitus RomaPendirian7 Desember 2002KatedralKatedral Gembala Baik NovalichesPelindungYesus, Gembala BaikKepemimpinan k...

István IVIstván IV digambarkan di Kronik PiktumRaja Hungaria dan Kroasiaditentang oleh István IIIBerkuasa1163–1165Penobatan27 Januari 1163PendahuluLászló IIPenerusIstván IIIInformasi pribadiKelahiranskt. 1133Kematian11 April (usia 31-32)Zemun, SerbiaWangsaWangsa ÁrpádAyahBéla II dari HungariaIbuIlonaPasanganMaria KomnenaAgamaKatolik Roma István IV (Hongaria: IV. Istváncode: hu is deprecated , Kroasia: Stjepan IVcode: hr is deprecated , bahasa Slowakia: Štefan IV; skt. 1133&#...

Motorways of PakistanPakistan motorway signSystem informationMaintained by National Highway AuthorityLength2,567 km (1,595 mi)Formed1997Highway namesSystem links Roads in Pakistan Motorways of Pakistan (Urdu: پاکستان کے موٹروے) are a network of multiple-lane, high-speed, controlled-access highways in Pakistan which are owned, maintained, and operated federally by Pakistan's National Highway Authority. Motorways were constructed during the 2013-2017 reign of Nawa...

陆军第十四集团军炮兵旅陆军旗存在時期1950年 - 2017年國家或地區 中国效忠於 中国 中国共产党部門 中国人民解放军陆军種類炮兵功能火力支援規模约90门火炮直屬南部战区陆军參與戰役1979年中越战争 中越边境冲突 老山战役 成都军区对越轮战 紀念日10月25日 陆军第十四集团军炮兵旅(英語:Artillery Brigade, 14th Army),是曾经中国人民解放军陆军第十四集团军下属�...

Pengatapan di Denmark Selatan Dalam konstruksi pembangunan, pengatapan adalah sebuah pengerjaan pembangunan secara tradisional di mana bagian terakhirnya ditempatkan di atas sebuah struktur. Sejarah Praktik tersebut masih umum di Britania Raya, Jerman, Austria, Republik Ceko, Slowakia, Polandia, dan Amerika Serikat Galeri Pengatapan (Wiecha) di Polandia Pengatapan di Norwegia (1959) Catatan Referensi John V. Robinson (2001). The 'topping out' traditions of the high-steel ironworkers Diarsipka...

Academy Awards ke-82Tanggal7 Maret 2010 (2010-03-07)TempatKodak TheatreHollywood, Los Angeles, CaliforniaPembawa acaraAlec BaldwinSteve Martin[1]Pembawa pra-acaraJess CagleKathy IrelandSherri Shepherd[2]ProduserBill MechanicAdam Shankman[3]Pengarah acaraHamish Hamilton[4]SorotanFilm TerbaikThe Hurt LockerPenghargaan terbanyakThe Hurt Locker (6)Nominasi terbanyakAvatar dan The Hurt Locker (9)Liputan televisiJaringanABCDurasi3 jam, 37 menit[5]Peringk...

Preserved Narrow-gauge 4-6-0 steam locomotive This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Southern Pacific 18 – news · newspapers · books · scholar · JSTOR (April 2019) (Learn how and when to remove this template message) Nevada-California-Oregon 12Southern Pacific 18SP No. 18 at Laws, California, in 201...

American rock band Marilyn MansonMarilyn Manson performing in 2017. From left to right: Paul Wiley, Tyler Bates, Manson, Daniel Fox and Twiggy Ramirez (Gil Sharone obscured at the drums)Background informationAlso known asMarilyn Manson & the Spooky Kids (1989–1993)OriginFort Lauderdale, Florida, U.S.Genres Industrial rock industrial metal gothic rock alternative metal shock rock Years active1989 (1989)–presentLabels Hell, etc. Loma Vista Caroline Concord Cooking Vinyl Interscope ...
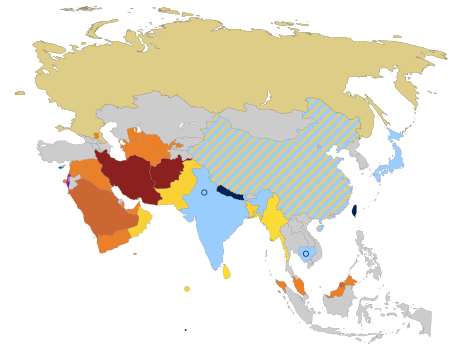
Part of the LGBT rights seriesLegal status ofsame-sex unions Marriage Andorra Argentina Australia Austria Belgium Brazil Canada Chile Colombia Costa Rica Cuba Denmark Ecuador Estonia Finland France Germany Greece Iceland Ireland Luxembourg Malta Mexico Nepal Netherlands1 New Zealand2 Norway Portugal Slovenia South Africa Spain Sweden Switzerland Taiwan United Kingdom3 United States4 Uruguay Recognized Israel5 Civil unions andregistered partnerships Bolivia Croatia Cyprus Czech Republic Hunga...

Голубянки Самец голубянки икар Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ПервичноротыеБез ранга:ЛиняющиеБез ранга:PanarthropodaТип:ЧленистоногиеПодтип:ТрахейнодышащиеНадкласс:ШестиногиеКласс...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Bagian dari seriIlmu Pengetahuan Formal Logika Matematika Logika matematika Statistika matematika Ilmu komputer teoretis Teori permainan Teori keputusan Ilmu aktuaria Teori informasi Teori sistem FisikalFisika Fisika klasik Fisika modern Fisika terapan Fisika komputasi Fisika atom Fisika nuklir Fisika partikel Fisika eksperimental Fisika teori Fisika benda terkondensasi Mekanika Mekanika klasik Mekanika kuantum Mekanika kontinuum Rheologi Mekanika benda padat Mekanika fluida Fisika plasma Ter...

1978 single by Elvis Costello For the Canadian musical group, see Radio Radio (band). Radio RadioSingle by Elvis Costello and the Attractionsfrom the album This Year’s Model B-sideTiny StepsReleased20 October 1978Recorded1978Genre New wave[1] power pop[2] Length3:04LabelRadar RecordsSongwriter(s)Elvis CostelloProducer(s)Nick LoweElvis Costello and the Attractions singles chronology This Year's Girl (1978) Radio Radio (1978) Oliver's Army (1979) Music videoRadio Radio” on Y...

Linea M5Logo La stazione di Garibaldi FS ReteMetropolitana di Milano Stato Italia CittàMilano Apertura2013 Ultima estensione2015 GestoreATM Sito webwww.metro-5.com CaratteristicheStazioni19 Lunghezza12,9[1] km Distanza mediatra stazioni678 m Tempo di percorrenza26 min Trazione750 V CC (tramite terza rotaia) Scartamento1 435 mm Materiale rotabileMetrò Automatico AnsaldoBreda (21 treni) Totale treni: 21 StatistichePasseggeri giornalieri119 280 Passeg...

British royal recognitions The 2021 New Year Honours are appointments by some of the 16 Commonwealth realms to various orders and honours to recognise and reward good works by citizens of those countries. The New Year Honours are awarded as part of the New Year celebrations at the start of January and those for 2021 were announced on 30 December 2020.[1][2] The recipients of honours are displayed as they were styled before their new honour and arranged by the country whose min...

Questa voce sull'argomento cestisti russi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Andrej DesjatnikovNazionalità Russia Altezza217 cm Peso98 kg Pallacanestro RuoloCentro Squadra Astana CarrieraGiovanili 2009-2010 Spartak Primor'e2011-2014 Triumf Ljubercy Squadre di club 2014-2019 Zenit S. Pietroburgo53 (127)2017-2018→ W.M. Szczecin16 (67)2019-2021 Chimki6 (...

Cadet branch of the House of Valois House of Valois-BurgundyParent houseHouse of ValoisCountry France BurgundyFounded6 September 1363 (1363-09-06)FounderPhilip the BoldFinal rulerMary of BurgundyTitles List Duke of Burgundy Duke of Lothier Duke of Brabant Duke of Limburg Duke of Luxemburg Duke of Lorraine Duke of Guelders Count of Flanders Count of Artois Count Palatine of Burgundy Count of Hainaut Count of Holland Count of Zeeland Count of Namur Count of Zutphen Coun...

Ancient Indo-European language of South Asia Sanskritसंस्कृत-, Saṃskṛta-, संस्कृतम्, Saṃskṛtam (top) A 19th-century illustrated Sanskrit manuscript from the Bhagavad Gita,[1] composed c. 400 – 200 BCE.[2][3] (bottom) The 175th-anniversary stamp of the third-oldest Sanskrit college, Sanskrit College, Calcutta, founded in 1824.Pronunciation[ˈsɐ̃skr̩tɐm]RegionSouth Asia (India proper), In...
この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典が不足しています。存命人物の記事は特に、検証可能性を満たしている必要があります。(2018年10月) 大言壮語的な記述になっています。(2018年10月) あまり重要でない事項が過剰に含まれているおそれがあり、整理が求められています。(2013年6月)出典検索?: 崎谷健次�...

Ancient Egyptian architectureTop: Great Pyramid of Giza (c. 2589–2566 BC); Centre: Columns of the Great Hypostyle Hall from the Temple of Karnak (c. 1294–1213 BC); Bottom: Temple of Isis from Philae (c. 380 BC-117 AD)Years activec. 3100 BC-300 AD Ancient Egyptianculture Architecture Art Clothing Cuisine Dance Literature vte Spanning over three thousand years, ancient Egypt was not one stable civilization but in constant change and upheaval, commonly split into periods by historians. Like...