Закон на Ом
|
Read other articles:

In classical Buddhist Cosmology, Akaniṣṭha (Pali: Akaniṭṭha, meaning Nothing Higher, Unsurpassed) is the highest of the Pure Abodes, and thus the highest of all the form realms. It is the realm where devas like Maheśvara live. In Mahayana Buddhism, Akaniṣṭha is also a name for the Pure Land (Buddhafield) of the Buddha Vairocana.[1] This is also the setting of the Ghanavyūha Sūtra. Vajradhara, the Sambhogakaya Buddha. Tibetan Buddhism, Akaniṣṭha (Tib. 'og min) often ...

Andreas E. MogensenLahir2 November 1976 (umur 47)[1]Copenhagen, DenmarkStatusAktifKebangsaanDenmarkNama lainAndreas Enevold MogensenPekerjaanInsinyur penerbanganKarier luar angkasaAntariksawan ESAMisiSoyuz TMA-18M/Soyuz TMA-16M Situs webandreasmogensen.esa.int Andreas Enevold Mogensen (lahir 2 November 1976) adalah seorang insinyur dan antariksawan asal Denmark. Ia adalah orang Denmark pertama yang terbang ke luar angkasa sebagai bagian dari program iriss.[2] Refere...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Falsanoeme cyrus Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Falsanoeme Spesies: Falsanoeme cyrus Falsanoeme cyrus adalah spesies kumbang tanduk panjang yang tergolong famili Cera...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Supafest – news · newspapers · books · scholar · JSTOR (May 2023) (Learn how and when to remove this template message)Music festival SupafestGenre Urban R&B hip-hop rap pop DatesAprilLocation(s)AustraliaAdelaide (2010)Brisbane (2010–2012)Melbourne (2010�...

Widespread outbreak of food poisoning 2017–2018 South Africa listeriosis outbreakThe outbreak was from processed meats produced by Enterprise Foods in Polokwane.LocationSouth AfricaDate2017 – March 2018Deaths216[1]Injured1,060 confirmed cases[1] The 2017–2018 South African listeriosis outbreak was a widespread outbreak of Listeria monocytogenes food poisoning that resulted from contaminated processed meats produced by Enterprise Foods, a subsidiary of Tiger Brands,[2...

American department store chain This article is about the department store. For other uses, see Kohl. Kohl's CorporationCompany typePublicTraded asNYSE: KSSS&P 600 componentIndustryRetailFoundedSeptember 12, 1962 (61 years ago) (1962-09-12) in Brookfield, Wisconsin, U.S.FounderMaxwell KohlHeadquartersMenomonee Falls, Wisconsin, U.S.Number of locations1,174 (As of Feb. 3, 2024)[1]Key peopleTom Kingsbury (CEO & Director)ProductsClothing, footwear, jewelry, bea...

L'escatologia islamica riguarda quegli aspetti (dogmatici e non) che nel sistema dei valori e delle credenze musulmane si preoccupano di indicare quale sia il destino del genere umano dopo la morte e la risurrezione voluta da Allah nel Giorno del Giudizio. L'assetto escatologico è, tutto sommato, abbastanza semplice e, nei suoi aspetti dogmatici tratta in successione il tormento della tomba, la Bilancia, il Ponte e il Bacino. Secondo l'escatologia islamica, sacrilegi sul Monte del Tempio...

Voce principale: Serie B. Questa pagina raccoglie statistiche e record significativi riguardanti il campionato di calcio italiano di Serie B. Indice 1 Evoluzione del campionato di Serie B 1.1 Campionati disputati 2 Squadre partecipanti 2.1 Esordio in Serie B 2.2 Assente ininterrottamente dalla Serie B dal... 2.3 Presente ininterrottamente in Serie B dal... 2.4 Livello attuale delle squadre partecipanti 2.5 Partecipazioni per regione 3 Albo d'oro 3.1 Ultima volta 1º posto 3.1.1 Squadre campi...

Live album by R.E.M. The topic of this article may not meet Wikipedia's notability guideline for music. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: ITunes Originals – R.E.M. – news · newspapers · books · ...

Questa voce o sezione sull'argomento gruppi musicali britannici non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce o sezione sull'argomento gruppi musicali non è ancora formattata secondo gli standard. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del ...

American animated television series Kid CosmicSeason 1 promotional posterGenre Superhero Sci-fi comedy Dramedy Action Adventure Created byCraig McCrackenBased onThe Kid from Planet Earthby Craig McCrackenDeveloped by Craig McCracken Francisco Angones Lauren Faust Voices of Jack Fisher Amanda C. Miller Lily Rose Silver Tom Kenny Fred Tatasciore Keith Ferguson Composers Andy Bean Edward Underhill (S3) Country of originUnited StatesOriginal languageEnglishNo. of seasons3No. of episodes24Producti...

ShūbunLecture dans un bosquet de bambous.1446. Encre et couleurs légères sur papier, L. 33,7 cmBiographieNaissance 1414Décès 1463KyotoNom dans la langue maternelle 周文Activités Peintre, moine bouddhisteAutres informationsA travaillé pour Shōkoku-jiMaître JosetsuŒuvres principales Hue of the Water, Light on the Peaks (d), Reading in a Bamboo Grove (d)modifier - modifier le code - modifier Wikidata Tenshō Shūbun, nom de pinceau : Ekkei, est un moine-peintre japonais du XVe&#...

Craigserie TV d'animazione Logo originale della serie Titolo orig.Craig of the Creek Lingua orig.inglese PaeseStati Uniti AutoreMatt Burnett, Ben Levin MusicheJeff Rosenstock StudioCartoon Network Studios ReteCartoon Network 1ª TV30 marzo 2018 – in corso Stagioni5 Episodi170 (in corso) Rapporto16:9 Durata ep.12 min Rete it.Cartoon Network 1ª TV it.24 settembre 2018 – in corso Dialoghi it.Elena Rizzo[N 1...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

1972 book by Del Martin and Phyllis Lyon Lesbian/Woman Cover of the first editionAuthorsDel Martin and Phyllis LyonCountryUnited StatesLanguageEnglishSubjectLesbian feminismPublisherGlide PublicationsPublication date1972Media typePrint (Hardcover and Paperback)Pages283ISBN978-0553235975OCLC506556 Lesbian/Woman (1972; second edition 1991) is a work by the feminist and gay rights activists Del Martin and Phyllis Lyon, in which the authors discuss what it means to be a lesbian. The book was...

Bendera Pribadi Ratu Jamaika Bendera Pribadi Ratu Jamaika adalah bendera pribadi Ratu Elizabeth II dalam peranannya sebagai Ratu Jamaika. Bendera ini telah disetujui untuk digunakan pada tahun 1962 dengan perbandingan sekitar 4:7~. Bendera ini hanya digunakan oleh Ratu ketika dia berada di Jamaika atau menghadiri acara di luar negeri dalam peranannya sebagai kepala negara Jamaika. Perwakilan Ratu, Gubernur-Jenderal Jamaika memiliki bendera tersendiri. Bendera ini terdiri dari bendera lambang ...

Contea di FranklinconteaLocalizzazioneStato Stati Uniti Stato federato Missouri AmministrazioneCapoluogoUnion Data di istituzione1818 TerritorioCoordinatedel capoluogo38°24′36″N 91°04′48″W38°24′36″N, 91°04′48″W (Contea di Franklin) Superficie2 410 km² Abitanti93 807 (2000) Densità38,92 ab./km² Altre informazioniFuso orarioUTC-6 CartografiaUnion Contea di Franklin – Mappa Sito istituzionaleModifica dati su Wikidata · Manuale La contea di...
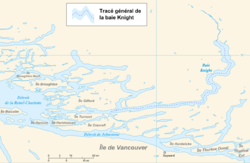
Waterway between northern Vancouver Island and mainland British Columbia, Canada Johnstone StraitFrench: Détroit de JohnstoneJohnstone Strait backdropped by the Vancouver Island RangesJohnstone StraitLocation in British ColumbiaMap of Johnstone Strait (bottom) and the surrounding islands and inletsLocationBritish Columbia, CanadaCoordinates50°28′0″N 126°05′0″W / 50.46667°N 126.08333°W / 50.46667; -126.08333TypeChannelOcean/sea sourcesPacific Ocean Johnston...

American Secret Service agent (1930–2015) Jerry ParrParr in 2013Born(1930-09-16)September 16, 1930Montgomery, Alabama, U.S.DiedOctober 9, 2015(2015-10-09) (aged 85)Washington, D.C., U.S.EducationVanderbilt UniversityLoyola UniversityOccupationSecret Service agentKnown forSaving President Reagan during the 1981 assassination attemptSpouse Carolyn Parr (m. 1959)Children3 Jerry S. Parr (September 16, 1930 – October 9, 2015) was a United States Secret...


































