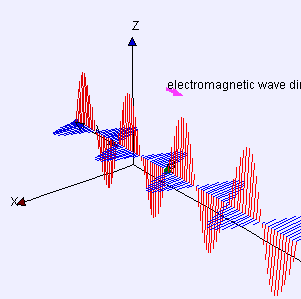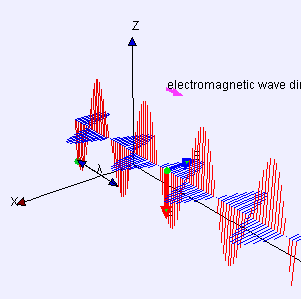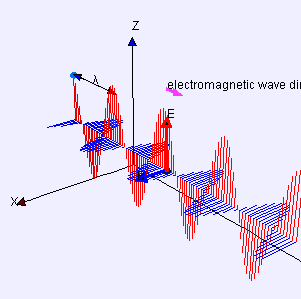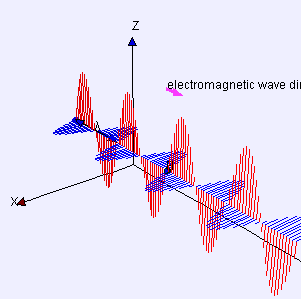
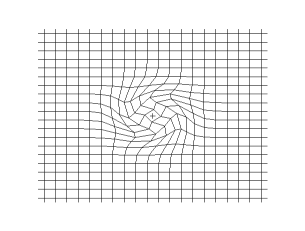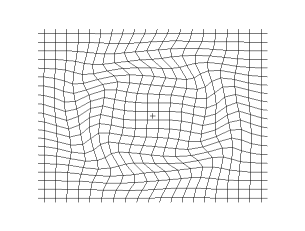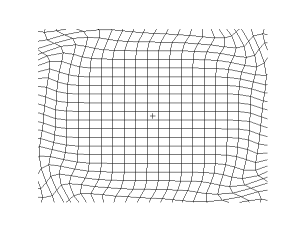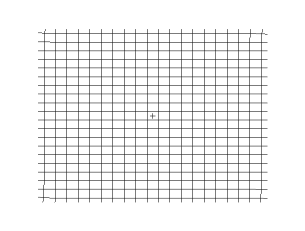
Transverse wave
|
Read other articles:

Tanggal dan waktu WU (UTC ±0)ekuinoks dan titik balik matahari di Bumi[1][2] peristiwa ekuinoks titik balik ekuinoks titik balik bulan Maret[3] Juni[4] September[5] Desember[6] tahun tanggal waktu tanggal waktu tanggal waktu tanggal waktu 2019 20 21:58 21 15:54 23 07:50 22 04:19 2020 20 03:50 20 21:43 22 13:31 21 10:03 2021 20 09:37 21 03:32 22 19:21 21 15:59 2022 20 15:33 21 09:14 23 01:04 21 21:48 2023 20 21:25 21 14:58 23 06:50 22 03:28 202...

Bagian dari seriGereja Katolik menurut negara Afrika Afrika Selatan Afrika Tengah Aljazair Angola Benin Botswana Burkina Faso Burundi Chad Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Guinea Khatulistiwa Jibuti Kamerun Kenya Komoro Lesotho Liberia Libya Madagaskar Malawi Mali Maroko Mauritania Mauritius Mesir Mozambik Namibia Niger Nigeria Pantai Gading Republik Demokratik Kongo Republik Kongo Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland ...

Thomas HovendenThe Last Moments of John Brown, 1882Naissance 28 décembre 1840DunmanwayDécès 14 août 1895 (à 54 ans)Plymouth MeetingNationalité américaineActivité PeintreFormation Académie américaine des beaux-artsMaître Alexandre CabanelMouvement École de Pont-AvenConjoint Helen Corson Hovenden (en)Signaturemodifier - modifier le code - modifier Wikidata Thomas Hovenden (28 décembre 1840 — 14 août 1895), est un peintre irlando-américain et un professeur. Il a peint des s...

العلاقات البولندية الوسط أفريقية بولندا جمهورية أفريقيا الوسطى بولندا جمهورية أفريقيا الوسطى تعديل مصدري - تعديل العلاقات البولندية الوسط أفريقية هي العلاقات الثنائية التي تجمع بين بولندا وجمهورية أفريقيا الوسطى.[1][2][3][4][5] مقارنة ب�...

Fahri Hamzah Wakil Ketua Dewan Perwakilan Rakyat Bidang Kesejahteraan RakyatMasa jabatan2 Oktober 2014 – 1 Oktober 2019PresidenSusilo Bambang Yudhoyono Joko WidodoKetua DPRSetya NovantoAde KomarudinBambang Soesatyo PendahuluTaufik KurniawanPenggantiMuhaimin Iskandar Informasi pribadiLahir10 November 1971 (umur 52)Utan, Sumbawa, Nusa Tenggara Barat, IndonesiaPartai politikPKS (2004–2016)Gelora (2019–)Orang tuaH. Hamzah Ahmad[1] (ayah)Alma materUniversitas IndonesiaS...

Combination medication Dextromethorphan/bupropionDextromethorphanBupropionCombination ofDextromethorphanNMDA receptor antagonist, σ1 receptor agonist, serotonin-norepinephrine reuptake inhibitor, nicotinic acetylcholine receptor negative allosteric modulator, and other actionsBupropionNorepinephrine–dopamine reuptake inhibitor and nicotinic acetylcholine receptor negative allosteric modulatorClinical dataTrade namesAuvelityOther namesDXM/BUP; AXS-05License data US DailyMed: Dextr...

Eberhard KoebelEberhard Koebel circa 1930Born(1907-06-22)22 June 1907Stuttgart, GermanyDied31 August 1955(1955-08-31) (aged 48)Berlin, GermanyOccupation(s)Youth leader, writer, publisher, tent designer and Nazi resister. Eberhard Koebel also Eberhard Köbel, called tusk,[1] i.e., the German in the language of the Sámi people he traveled among,[2][3] (22 June 1907 – 31 August 1955) was a German youth leader, writer, and publisher. Eberhard Koebel was born in St...

Kitab Kells, ~ 800 M, ditulis dengan huruf-huruf yang dikenal berjenis insular majuscule, suatu variasi tulisan uncial yang berasal dari Irlandia. Uncial adalah jenis tulisan tangan yang seluruhnya menggunakan hanya huruf besar (Inggris: upper case, large letters, capital letters, capitals, caps, majuscule, upper-case, atau uppercase) yang umum digunakan dari abad ke-4 sampai ke-8 M[1] oleh para jurutulis untuk membuat naskah bahasa Latin dan bahasa Yunani Bizantin.[2] Hur...

You're Mine (Eternal)Lagu oleh Mariah Careydari album Me. I Am Mariah... The Elusive ChanteuseDirilis12 Februari 2014 (2014-02-12)FormatUnduh digitalPenyiaran radioDirekamRapture StudiosMetrocity StudiosJungle City StudiosStudio di PalmsGenreR&BDurasi3:44LabelDef JamPenciptaMariah CareyRodney JerkinsProduserCareyDarkchild You're Mine (Eternal) adalah lagu dari musisi ternama Amerika Serikat, Mariah Carey dari album studionya yang keempat belas, Me. I Am Mariah... The Elusive Chanteus...

American baseball player (born 1996) Baseball player Seth BeerBeer with the Fayetteville Woodpeckers in 2019Pittsburgh Pirates Outfielder / First basemanBorn: (1996-09-18) September 18, 1996 (age 27)Maryville, Illinois, U.S.Bats: LeftThrows: RightMLB debutSeptember 10, 2021, for the Arizona DiamondbacksMLB statistics (through 2022 season)Batting average.208Home runs2Runs batted in12 Teams Arizona Diamondbacks (2021–2022) Career highlights and awards Dick Howser Trophy (2...

Sinagoga Quai Kléber di StrasburgoSynagogue Consistoriale du quai Kléber de StrasbourgStato Francia LocalitàStrasburgo Coordinate48°35′07.18″N 7°44′31.61″E / 48.585329°N 7.742113°E48.585329; 7.742113Coordinate: 48°35′07.18″N 7°44′31.61″E / 48.585329°N 7.742113°E48.585329; 7.742113 ReligioneEbraismo ArchitettoLudwig Levy Stile architettoniconeoromanica Inizio costruzione1896 Completamento1898 Demolizione1940 Modifica dati su Wikid...

Untuk pengertian lain, lihat Utica. Lokasi Utica di negara bagian New York bagian utara Utica (bahasa Tuscarora: Yunę́ˀnare•θ) adalah sebuah kota yang terletak di negara bagian New York, Amerika Serikat. Utica adalah county seat (ibu kota) untuk Oneida County. Populasi dari masa ke masa [1] Tahunsensus Populasi 1840 12.782 1850 17.565 1860 22.529 1870 28.804 1880 33.914 1890 44.007 1900 56.383 1910 74.419 1920 94.156 1930 101.740 1940 100.518 1950 100.489 1960 100.410* 1970 91.611* 1980...
Ciccio Ingrassia nel 1967, in un fotogramma del film Il lungo, il corto, il gatto Francesco Ingrassia, detto Ciccio (Palermo, 5 ottobre 1922 – Roma, 28 aprile 2003), è stato un attore, comico, regista, sceneggiatore[1][2], conduttore televisivo e cantante italiano. Insieme a Franco Franchi formò il famoso duo comico Franco e Ciccio, entrato nella storia della cinematografia italiana.[3] La coppia girò più di 100 film tra gli anni sessanta e ottanta, e si distinse...

لمعانٍ أخرى، طالع كلية الحقوق (توضيح). كلية الحقوق شعار كلية الحقوق (الجامعة الأردنية)شعار الكلية. مبنى الكلية. الشعار الحق يعلو ولا يُعلى عليه. معلومات التأسيس 1976 (منذ 48 سنة) النوع كلية جامعية حكومية الشُعب قسمان الموقع الجغرافي إحداثيات 32°01′07″N 35°52′20″E / 32.0...

Laguna Wattamola Koordinat: 34°08′15″S 151°07′04″E / 34.13750°S 151.11778°E / -34.13750; 151.11778 Wattamola, juga dikenal sebagai Pantai Wattamola, adalah sebuah teluk kecil, laguna, dan pantai di pesisir New South Wales, wilayah selatan Sydney, daerah ini termasuk dalam kawasan konservasi Royal National Park. Sejarah Wattamola adalah nama Aborigin untuk daerah tersebut, yang berarti tempat di dekat air mengalir.[1] Nama itu dicatat sebagai Watta-M...

SenateDominion of CeylonTypeTypeUpper house HistoryEstablished1947Disbanded2 October 1971Preceded byState Council of CeylonSucceeded byNoneSeats30Meeting placeThe old Legislative Council building in Colombo Fort that used to house the Senate. Today it is known as the Republic Building and houses the Ministry of Foreign Affairs. Politics of Sri Lanka Constitution Previous constitutions: 1931 · 1947 Law of Sri Lanka Human rights Law enforcement GovernmentExecutive President (List) Pr...

Ongoing COVID-19 viral pandemic in Syria COVID-19 pandemic in SyriaDiseaseCOVID-19Virus strainSARS-CoV-2First outbreakWuhan, Hubei, ChinaArrival date22 March 2020(4 years, 2 months, 3 weeks and 1 day)Confirmed cases• 57,743 (Government reported only) • 13,690 (needs update) (Including Interim Government and Rojava Administration reported cases)Active cases0Recovered54,578Deaths3,165Fatality rate5.80%TerritoriesАll 14 governorates (All government and non-government rep...

Mayu IshikawaNazionalità Giappone Altezza174 cm Pallavolo RuoloSchiacciatrice Squadra AGIL CarrieraGiovanili 2016-2019 Shimokitazawa Seitoku Squadre di club 2019-2023 Toray Arrows2023-2024 Firenze2024- AGIL Nazionale 2017 Giappone U-182019 Giappone U-202019- Giappone Palmarès Campionato asiatico e oceaniano OroCorea del Sud 2019 Coppa del Mondo BronzoGiappone 2023 Statistiche aggiornate al 14 maggio 2024 Modifica dati su Wikidata ·...

City in North Yorkshire, England This article is about the city in England. For other uses, see Ripon (disambiguation). City in EnglandRiponCityClockwise from top left: the Market Place, Ripon Cathedral, Newby Hall, Fountains Abbey and the Cabmen's ShelterCoat of armsRiponLocation within North YorkshirePopulation16,702 (2011 census)[1]OS grid referenceSE312714• London227 mi (365 km) SSECivil parishRiponUnitary authorityNorth YorkshireCeremonia...

Derby CountyTên đầy đủDerby County Football ClubBiệt danhThe Rams The sheepThành lập5 tháng 2 năm 1884bởi William MorleySânPride Park, DerbySức chứa33,597Chủ tịch điều hànhAndrew ApplebyHuấn luyện viênLiam Rosenior (tạm quyền)[1][2]Giải đấuEFL League One2021–22EFL Championship, 23 trên 24 (xuống hạng)Trang webTrang web của câu lạc bộ Màu áo sân nhà Màu áo sân khách Màu áo thứ ba Mùa giải hiện nay Derby C...