Perimeter
|
Read other articles:

The United States Federal Bureau of Investigation has a number of bureaucratic forms that must be filled out in the commission of any activities by its agents. These are typically mandatory, and are often presented at legal hearings as evidence of context. FD-209 An FD-209 form is used by FBI agents to record their contacts with unofficial criminal informants.[1] FD-292 An FD-292 form is used by FBI agents to notify the agency that they are getting married or divorced.[2] FD-...

Marathi cinema All-time 1910s 1910-1919 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 19841985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 19941995 1996 1997 1998 1999 2000s 2000 2001 ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Dicky Satria – berita · surat kabar · buku · cendekiawan · JSTOR Dicky SatriaLahir4 Maret 1992 (umur 32)Bandung, Jawa Barat, IndonesiaPekerjaan Aktor Pemeran Tahun aktif2019—sekarang Dicky Sa...
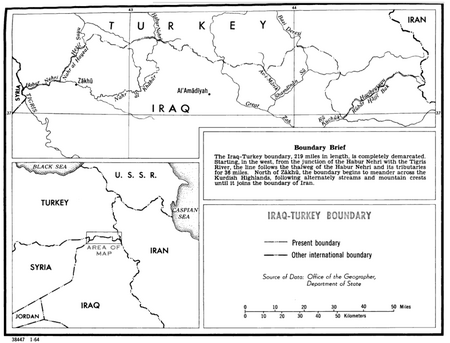
International border Between the Republic Of Turkey And The Republic Of Iraq Iraq-Turkey borderالحدود العراقية التركيةIrak–Türkiye sınırıCharacteristicsEntities Iraq TurkeyLength378 km (235 mi)[1] Map of the Iraq–Turkey border The Iraq–Turkey border (Kurdish: Sînorê Îraqê–Tirkiye, Arabic: الحدود العراقية التركية, romanized: alhudud aleiraqiat alturkia, Turkish: Irak–Türkiye sınırı) is 367 km...

Pour les articles homonymes, voir Oscillateur. Un oscillateur intégré à quartz. Un oscillateur électronique est un circuit dont la fonction est de produire un signal électrique périodique, de forme sinusoïdale, carrée, en dents de scie, ou quelconque. L'oscillateur peut avoir une fréquence fixe ou variable. Il existe plusieurs types d'oscillateurs électroniques ; les principaux sont : oscillateurs à circuit LC et un étage amplificateur, HF le plus souvent ; oscilla...

Tatong Bara Wali Kota Kotamobagu ke-2Masa jabatan25 September 2018 – 25 September 2023PresidenJoko WidodoGubernurOlly DondokambeyWakilNayodo Koerniawan PendahuluAdnan Massinae (Plh.)PenggantiAsripan Nani (Penjabat Walikota)Masa jabatan22 September 2013 – 22 September 2018PresidenSusilo Bambang YudhoyonoJoko WidodoGubernurSinyo Harry SarundajangOlly DondokambeyWakilJainuddin Damopolii PendahuluDjelantik MokodompitPenggantiAdnan Massinae (Plh.)Wakil Wali Kota Kotamobag...

تروي شعار الإحداثيات 42°43′54″N 73°41′33″W / 42.731666666667°N 73.6925°W / 42.731666666667; -73.6925 [1] تاريخ التأسيس 1787 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة رينسيلير عاصمة لـ مقاطعة رينسيلير خصائص جغرافية المساحة 28....

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

Australian IdolAustralian IdolPembuat Simon FullerJuri Mark Holden Marcia Hines Ian Dickson(2003–04, 2007–) Kyle Sandilands(2005–)Negara asal AustraliaProduksiProduser eksekutifGreg Benness Suzanne MitchellLokasi produksiFOX Studios, Sydney Sydney Opera House (Finale)Rilis asliJaringanNetwork TenFormat gambar1080i (HDTV)Format audioDolby Digital 5.1RilisJuly 27, 2003 –starring Andrew G James Mathison Peserta Australian Idol(dengan tanggal tereliminasi) Musim Pertama (2003) ...

Zgorzelec Polandia > Provinsi Dolnoslaskie Motto: ? Hari jadi 1948 Wali kota Rafał Gronicz Wilayah 16 km² Penduduk -Kepadatan 33.278 jiwa (2004)2098 / km2 Situs web resmi: [1] Diarsipkan 2005-08-29 di Wayback Machine. Zgorzelec dilafazkan sebagai [zgɔˈʒɛlɛʦ] (Jerman Ost-Görlitz, Sorbia Zhorjelc) adalah kota di Polandia di tepi sungai Neiße, di provinsi Dolnośląskie, di seberang kota Jerman Görlitz, yang merupakan bagian barat kota ini sampai 1945. Menurut sejarah ko...

Voce principale: Torino Football Club. AC TorinoStagione 1953-1954Sport calcio Squadra Torino Direttore Tecnico Jesse Carver[1], poi Annibale Frossi Allenatore Oberdan Ussello[1], poi Luigi Miconi PresidenteComitato di reggenza[2] Serie A9º Maggiori presenzeCampionato: Farina (34) Miglior marcatoreCampionato: Buhtz (11) StadioFiladelfia 1952-1953 1954-1955 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associazione Cal...

Eingang Hilton Berlin Das Hilton-Gebäude von 1958, seit 1978 InterContinental Berlin Hilton Berlin Foyer Das Hilton Berlin ist ein Luxushotel der Hilton Worldwide Gruppe in Berlin. Es ist Berlins größtes Fünf-Sterne-Hotel.[1] Inhaltsverzeichnis 1 Hotel 2 Geschichte 3 Weblinks 4 Einzelnachweise Hotel Das Hotel hat 601 Zimmer und Suiten,[2] zwei Restaurants und eine Lobby Lounge. Der Wellnessbereich ist 800 m² groß. Es gibt 15 Veranstaltungsräume und einen 488 m² großen...

Vajubhai Vala Gubernur KarnatakaPetahanaMulai menjabat 1 September 2014[1]PendahuluKonijeti RosaiahPenggantiPetahanaJurubicara Mahkamah Legislatif GujaratMasa jabatan23 Januari 2013 – 30 Agustus 2014PendahuluGanpat VasavaPenggantiMangubhai C. Patel (pelaksana jabatan)Anggota Mahkamah Legislatif GujaratMasa jabatan26 Desember 2012 – 30 Agustus 2014Daerah pemilihanRajkot West Informasi pribadiLahir23 Januari 1938 (umur 86)Partai politikPartai Bharatiya Jan...

2022 Illinois Attorney General election ← 2018 November 8, 2022 2026 → Nominee Kwame Raoul Tom DeVore Party Democratic Republican Popular vote 2,219,420 1,774,468 Percentage 54.35% 43.45% County results Congressional district resultsRaoul: 40–50% 50–60% 70–80%DeVore: 40–50% 50–60% &#...

Reverendus PaterPetrus Josephus ZoetmulderS.J.Piet ZoetmulderGerejaGereja Katolik RomaImamatTahbisan imam15 Agustus 1938Informasi pribadiNama lahirPetrus Josephus ZoetmulderLahir(1906-01-29)29 Januari 1906Utrecht (Utrecht), BelandaWafat8 Juli 1995(1995-07-08) (umur 89)Yogyakarta, IndonesiaKewarganegaraanIndonesiaDenominasiKatolik Roma Prof. Dr. Petrus Josephus Zoetmulder, S.J. (29 Januari 1906 – 8 Juli 1995) adalah seorang pakar Sastra Jawa dan budayawan Indonesia. Ia ter...

Season of television series Season of television series StarDanceSeason 9Celebrity winnerJiří DvořákProfessional winnerLenka Nora Návorková No. of episodes10ReleaseOriginal networkČeská televizeOriginal releaseOctober 13 (2018-10-13) –December 15, 2018 (2018-12-15)Season chronology← PreviousSeason 8 Next →Season 10 The 9th StarDance series was premiered on October 13, 2018 and ended on December 15, 2018.[1][2] Hosts in this series are aga...

Series of comic books This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nintendo Comics System – news · newspapers · books · scholar · JSTOR (October 2008) (Learn how and when to remove this message) Nintendo Comics SystemCover of the first issue The Nintendo Comics System was a series of comic books published...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2016) 10-يارد فايت10-Yard Fight 10ヤードファイト صورة من اللعبة لنظام آركيد المطور إريم الناشر تايتو النظام نينتندو إنترتينمنت سيستمإم إس إكسسيغا ساترن[1]بلاي ست�...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...




















![{\displaystyle \gamma :[0,2\pi ]\to \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9c3de071bb1d54124df8bdd8269abab594263c)







![{\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1d326a550ef41246054e0311de07e1375d535f3)










