Minimal prime ideal
|
Read other articles:

Halaman ini berisi artikel tentang musisi. Untuk tokoh lain bernama James Blake, lihat James Blake. James BlakeBlake pentas di Melt! Festival 2013Informasi latar belakangNama lahirJames Blake LitherlandNama lainHarmonimixOne-Take BlakeLahir26 September 1988 (umur 35)London, InggrisGenreElektronikR&BUK basssoulpost-dubsteppopPekerjaanPenyanyipenulis lagumulti-instrumentalisproduser rekamanInstrumenVokalpianosynthesizerTahun aktif2009–kiniLabel1-800 DinosaurR&SATLASA&MPolydor...
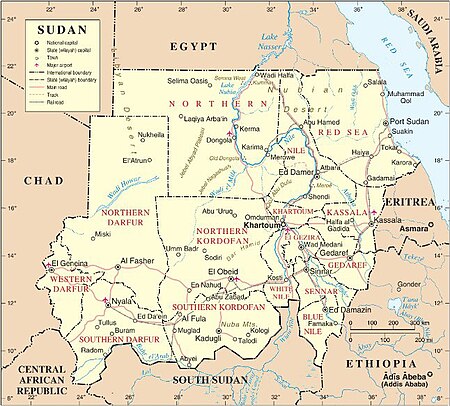
Geographic area in Sudan Nuba Mountainsجبال النوبة Jabal an-NūbāThe Nuba MountainsHighest pointElevation1,325 m (4,347 ft)Coordinates12°1′N 31°6′E / 12.017°N 31.100°E / 12.017; 31.100DimensionsLength145 km (90 mi)Width64 km (40 mi)GeographyLocation in Africa CountrySudan, South SudanRegionSouth Kordofan Map of Sudan (after 2011). The Nuba Mountains are labeled in Southern Kordofan The Nuba Mountains (Arabic: جبا...

Prime Minister of Sudan (2022–present) You can help expand this article with text translated from the corresponding article in Spanish. (April 2022) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machin...

Massachusetts state politician Jeff TurcoMember of the Massachusetts House of Representativesfrom the 19th Suffolk districtIncumbentAssumed office April 7, 2021Preceded byRobert DeLeo Personal detailsBornJeffrey Rosario TurcoRevere, Massachusetts, U.S.Political partyDemocraticChildren6EducationUniversity of Massachusetts Amherst (BA)Quinnipiac University (JD) Jeffrey Rosario Turco is an American attorney, politician, and former law enforcement officer serving as a member of th...

Cette page concerne l'année 1181 du calendrier julien. Chronologies Jayavarman VII.Données clés 1178 1179 1180 1181 1182 1183 1184Décennies :1150 1160 1170 1180 1190 1200 1210Siècles :Xe XIe XIIe XIIIe XIVeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Religion (,) et * Croisades Science () et Santé et médecine Terrorisme Calendriers Romain Chinois Grégorien Julien Hébraïque Hindou Hégirien Per...

American game show host JD RobertoBornJohn David Roberto (1969-10-23) October 23, 1969 (age 54)White Plains, New York, U.S.EducationNYU's Tisch School of the Arts (Bachelor of Fine Arts degree in Acting), University of British Columbia (Master of Fine Arts degree in Writing for Stage and Screen)Occupation(s)Television personality, writer, host, producerKnown forHosting Battle of the Ages, Daily Burn 365, Better, How To Get The Guy, Are You Hot?, Outback Jack, The Alaskan Adventure C...

January 2017 North American ice stormThe storm system over the United States as viewed by GOES-16 on January 15, 2017 TypeExtratropical cycloneWinter stormIce stormTornado outbreakFormedJanuary 10, 2017DissipatedJanuary 17, 2017 Lowest pressure1006 mb (29.71 inHg) Tornadoesconfirmed11Max. rating1EF2 tornado Maximum snowfallor ice accretionSnow – 29.5 inches (75 cm) at Red Mountain Pass, Colorado[1]Ice – 1.00 inch (2.5 cm) in Beaver, Oklahoma Fatalities9 fatalit...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

British record producer Not to be confused with Andy Richards (The Young and the Restless). This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Andy Richards – news · newspapers · books · scholar · ...

Eurovision Song Contest 2017Country NetherlandsNational selectionSelection processInternal selectionSelection date(s)Artist: 29 October 2016Song: 3 March 2017Selected entrantO'G3NESelected songLights and ShadowsSelected songwriter(s)Rory de KievitRick VolFinals performanceSemi-final resultQualified (4th, 200 points)Final result11th, 150 pointsNetherlands in the Eurovision Song Contest ◄2016 • 2017 • 2018► The Netherlands participated in the Eur...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Questa voce sull'argomento calciatori norvegesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Asle Arntsen Nazionalità Norvegia Calcio Ruolo Centrocampista CarrieraSquadre di club1 1965-1976 Fredrikstad131 (8)Nazionale 1966 Norvegia U-191 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Statist...

1964 Indian filmKohraa कोहराDirected byBiren NagWritten byDhruva ChatterjeeProduced byHemant KumarStarringWaheeda Rehman Biswajeet Lalita PawarCinematographyMarshall BraganzaMusic byHemant KumarKaifi Azmi (lyrics)ProductioncompanyGeetanjali FilmsRelease date 1964 (1964) Running time153 minutesCountryIndiaLanguageHindi Kohraa (The Fog) is a 1964 Indian thriller horror film directed by Biren Nag, starring Waheeda Rehman, Biswajeet and Lalita Pawar. The film was adapted from Daph...

Ukrainian ethnic minority in Russia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ukrainians in Russia – news · newspapers · books · scholar · JSTOR (August 2017) (Learn how and when to remove this message) Ethnic group Ukrainians in RussiaTotal population884 007 (2021)LanguagesRussian (99.8%, 2002), Ukrai...

Skye Terrier For the novel, see Greyfriars Bobby (novel). For the film, see Greyfriars Bobby (film). Greyfriars BobbyThis statue of Bobby sits at the corner of Edinburgh's Candlemaker Row and George IV Bridge, and is a Category A listed buildingBreedSkye Terrier or Dandie Dinmont Terrier[1]Born4 May 1855Edinburgh, Scotland [citation needed]Died14 January 1872 (aged 16)Edinburgh, ScotlandResting placeGreyfriars KirkyardKnown forGuarding the grave of his owner until he died...

Miss IndonesiaLogo Miss IndonesiaTanggal pendirian2005TipeKontes kecantikanKantor pusat JakartaLokasi IndonesiaJumlah anggota Miss World(2006-sekarang)Miss ASEAN (2005)Bahasa resmi IndonesiaChairwoman and FounderLiliana TanoesoedibjoTokoh pentingMartha TilaarWulan TilaarLina PriscillaSitus webwww.missindonesia.co.id Miss Kalimantan Utara adalah sebuah gelar yang didapat bagi perwakilan provinsi Kalimantan Utara di ajang Miss Indonesia. Pemegang titel saat ini adalah Kaetlyn William yang ...

Motor vehicle Fiat Tipo 70OverviewManufacturerFiatProduction1915–1920Body and chassisBody styleSedanLayoutFR layoutPowertrainEnginestraight-4 2001 cc[1]Transmission4-speed manualDimensionsWheelbase2,706 mm (107 in)[1]Length3,820 mm (150 in)[1]Curb weight1,735 kg (3,825 lb)[1]ChronologyPredecessorFiat ZeroSuccessorFiat 501 The Fiat 70 was a car produced by Italian car manufacturer Fiat between 1915 and 1920. The 70 ...

Megaregion in Arizona, United States This article is about the Arizona megaregion. For the similarly named metropolitan area, see Valley of the Sun. Megaregion of the U.S. in Arizona, USArizona Sun CorridorMegaregion of the U.S. Counter-clockwise from top: downtown Phoenix skyline, downtown Tucson, Mesa City Hall PhoenixTucsonSierra VistaCasa GrandeNogalesPrescottclass=notpageimage| Selected cities of the Arizona Sun CorridorCoordinates: 33°N 112°W / 33°N 112°W / 3...

Kalla PashaPasha dalam Film Fun, 1922LahirJoseph T. Rickard (1879-03-05)5 Maret 1879Detroit, Michigan, ASMeninggal10 Juni 1933(1933-06-10) (umur 54)Talmage, California, ASPekerjaanPegulat, vaudevillian, pemeranTahun aktif1919–1931 Kalla Pasha (5 Maret 1879 – 10 Juni 1933) adalah seorang pemeran, pelawak dan pegulat profesional asal Amerika Serikat. Ia aktif pada era film bisu. Filmografi pilihan The Wicked Darling (1919) Love, Honor and Behave (1920) Down on the F...

City in Illinois, United StatesGalvaCityNickname: City of GoLocation of Galva in Henry County, Illinois.Location of Illinois in the United StatesCoordinates: 41°10′0″N 90°2′32″W / 41.16667°N 90.04222°W / 41.16667; -90.04222CountryUnited StatesStateIllinoisCountyHenryArea[1] • Total2.75 sq mi (7.13 km2) • Land2.75 sq mi (7.13 km2) • Water0.00 sq mi (0.00 km2)Elevat...



![{\displaystyle \mathbb {C} [x,y]/(xy)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fc69a7bc41282794b565e67a32951d9641e5ba0)
![{\displaystyle \mathbb {C} [x,y]\to \mathbb {C} [x,y]/(xy)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec09d13cc4ae0e6854ff22fe6506593c63c0d270)



![{\displaystyle \mathbb {C} [x,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef7ee3803a8b93634fdfd422434c5952867b767e)



![{\displaystyle A=\mathbb {C} [x,y]/(x^{3}y,xy^{3})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6efe605d008cc546383c5781800ffdfb562b0df1)
























