Minimal polynomial of 2cos(2pi/n)
|
Read other articles:

Klorobi Chlorobi Bakteri belerang hijau dalam kolom WinogradskyTaksonomiSuperdomainBiotaDomainBacteriaSubkerajaanNegibacteriaFilumChlorobi Kelas, ordo, famili, genus Kelas Chlorobia Cavalier-Smith 2002 Ordo Chlorobiales Gibbons dan Murray 1978 Famili Chlorobiaceae Copeland 1956 Ancalochloris Gorlenko and Lebedeva 1971 Chlorobaculum Imhoff 2003 Chlorobium Nadson 1906 emend. Imhoff 2003 Chloroherpeton Gibson et al. 1985 Clathrochloris Witt et al. 1989 Pelodictyon Lauterborn 1913 Prosthecochlori...

Idols Netherlands Idols Netherlands Finalis(beserta tanggal tereliminasi) Musim Pertama (2003) Jamai LomanJuara Jim Bakkum9 Maret Hind Laroussi2 Maret Dewi Pechler23 Februari David Gonçalves16 Februari Marieke Van Ginneken9 Februari Bas Nibbelke2 Februari Joël De Tombe26 Januari Yuli Minguel19 Januari Zosja El Rhazi12 Januari Musim Kedua (2004) Boris TitulaerJuara Maud Mulder1 Mei JK24 April Marlies Schuitenmaker17 April Irma Van Pamelen10 April Eric Bouwman3 April Alice Hoes27 Maret Ron L...

كارل لودفيغ فيلدينوف (بالألمانية: Carl (Karl) Ludwig von bear) معلومات شخصية الميلاد 22 أغسطس 1765(1765-08-22)برلين الوفاة 10 يوليو 1812 (46 سنة)برلين الإقامة مملكة بروسيا مواطنة مملكة بروسيا عضو في الأكاديمية الملكية السويدية للعلوم، والأكاديمية البروسية للعلوم، والأكاديمية البا...

Mario Scaramella Mario Scaramella (lahir 23 April 1970)[1] adalah seorang pengacara, akademikus dan konsultan keamanan Italia yang menjadi terkenal di dunia internasional pada 2006 dalam kaitannya dengan peracunan bekas agen FSB Alexander Litvinenko. Scaramella bertugas sebagai penyelidik dan penasihat untuk Komisi Mitrokhin yang kontroversial yang dibentuk oleh partai Forza Italia yang dipimpin Silvio Berlusconi untuk menyelidiki dugaan kaitan antara lawan-lawan politik Berlusconi, t...
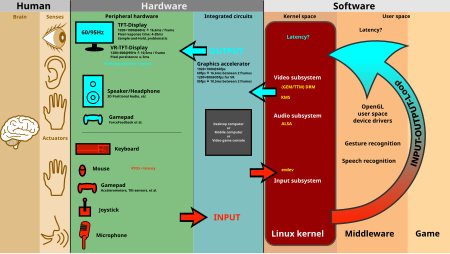
Academic discipline studying the relationship between computer systems and their users This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Human–computer interaction – news · ...

Japanese media franchise The Kabocha WineCover of the first manga volumeTheかぼちゃワイン(The Kabocha Wain) MangaWritten byMitsuru MiuraPublished byKodanshaMagazineWeekly Shōnen MagazineDemographicShōnenOriginal run1981 – 1984Volumes18 MangaThe Kabocha Wine — SequelWritten byMitsuru MiuraPublished bySeirindoPublishedOctober 15, 2006Volumes1 MangaThe Kabocha Wine — AnotherWritten byMitsuru MiuraPublished byAkita ShotenMagazinePlay ComicDemographicSe...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Chemical compound N-Ethyl-3-piperidyl benzilateLegal statusLegal status DE: Anlage I (Authorized scientific use only) US: Schedule I Identifiers IUPAC name (1-ethylpiperidin-3-yl) 2-hydroxy-2,2-di(phenyl)acetate CAS Number3567-12-2 YPubChem CID62504ChemSpider56281 YUNII02J52696MZChEMBLChEMBL342669 YChemical and physical dataFormulaC21H25NO3Molar mass339.435 g·mol−13D model (JSmol)Interactive image SMILES O=C(OC1CCCN(CC)C1)C(O)(c2ccccc2)c3ccccc3 InChI InChI=1S/...

بطولة أمم أوروبا لكرة القدم 1988تفاصيل المسابقةالبلد المضيف ألمانيا الغربيةالتواريخ10 يونيو – 25 يونيوالفرق8الأماكن8 (في 8 مدن مضيفة)المراكز النهائيةالبطل هولنداالوصيف الاتحاد السوفيتيإحصائيات المسابقةالمباريات الملعوبة15الأهداف المسجلة34 (2٫27 لكل مباراة)ا�...

Questa voce sull'argomento cestisti giamaicani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Garfield Blair Nazionalità Stati Uniti Giamaica Altezza 196 cm Peso 93 kg Pallacanestro Ruolo Guardia Termine carriera 2016 CarrieraGiovanili 2005-2009 Stetson HattersSquadre di club 2012Kilsyth Cobras2013Heartland Eagles2013-2014 Cáceres18 (176)2014-2015 Peixefresco34 (467)2015-20...

This article is about the year 1215. For aviation frequency 121.5, see Aircraft emergency frequency. Calendar year Millennium: 2nd millennium Centuries: 12th century 13th century 14th century Decades: 1190s 1200s 1210s 1220s 1230s Years: 1212 1213 1214 1215 1216 1217 1218 1215 by topic Leaders Political entities State leaders Religious leaders Birth and death categories Births – Deaths Establishments and disestablishments categories Establishments – Disestablishments ...

سليم كندي تقسيم إداري البلد إيران [1] إحداثيات 37°40′26″N 45°06′42″E / 37.67388889°N 45.11166667°E / 37.67388889; 45.11166667 السكان التعداد السكاني 26 نسمة (إحصاء 2016) الرمز الجغرافي 18525 تعديل مصدري - تعديل سليم كندي هي قرية في مقاطعة أرومية، إيران.[2] يقدر عدد سكانها ب...

Judging another culture solely by the values and standards of one's own culture Polish sociologist Ludwig Gumplowicz is believed to have coined the term ethnocentrism in the 19th century, although he may have merely popularized it. Ethnocentrism in social science and anthropology—as well as in colloquial English discourse—means to apply one's own culture or ethnicity as a frame of reference to judge other cultures, practices, behaviors, beliefs, and people, instead of using the standards ...

Disambiguazione – Show rimanda qui. Se stai cercando altri significati, vedi Show (disambigua). Questa voce sull'argomento spettacolo è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Il Festival mundial de Tango a Buenos Aires Lo spettacolo è un evento naturale o antropico, spontaneo o provocato o anche un'imitazione di questo, che cattura l'attenzione di una o più persone che fungono da spettatori ovvero soggetti testimoni in genere aventi...

ASUS Eee PC adalah model komputer jinjing berukuran kecil yang dirancang dan diproduksi oleh perusahaan ASUS. Perbedaan utama ASUS Eee PC dengan kebanyakan komputer jinjing lain terletak pada ukuran fisik yang lebih kecil, bobot yang lebih ringan, serta spesifikasi teknis yang dimilikinya. Pada awal peluncuran produknya, Eee PC menggunakan sistem operasi Linux dan perangkat penyimpan data berupa memori solid-state drive (SSD). Pada model-model Eee PC berikutnya, sistem operasi Windows XP dise...

American musician (born 1945) Bobby OgdinBobby Ogdin at Nashville's Ryman Auditorium October, 2018Background informationBirth nameRobert Ford OgdinBorn (1945-09-28) September 28, 1945 (age 78)Detroit, Michigan, USAGenrescountry, rock, alternative rockOccupation(s)keyboardist, non-vocal instrumentalistInstrument(s)KeyboardsYears active1975–presentWebsitebobbyogdin.comMusical artistRobert Ford Ogdin (born September, 1945) is a Nashville-based recording session pianist. He is best known a...

Graph that misrepresents data Example of a truncated (left) vs full-scale graph (right), using the same data Part of a series on StatisticsData and information visualization Major dimensions Exploratory data analysis Information design Interactive data visualization Descriptive statistics Inferential statistics Statistical graphics Plot Data analysis Infographic Data science Important figures Tamara Munzner Ben Shneiderman John Tukey Edward Tufte Simon Wardley Hans Rosling David McCandless Ki...

1975 South African Grand Prix Race detailsDate 1 March 1975Official name XXI Lucky Strike Grand Prix of South AfricaLocation KyalamiTransvaal Province, South AfricaCourse Permanent racing facilityCourse length 4.104 km (2.550 miles)Distance 78 laps, 320.112 km (198.908 miles)Weather SunnyPole positionDriver Carlos Pace Brabham-FordTime 1:16.41[1]Fastest lapDriver Carlos Pace Brabham-FordTime 1:17.20[2] on lap 11PodiumFirst Jody Scheckter Tyrrell-FordSecond Carlos Reutemann Br...

Zach Sherwin Sherwin pada tahun 2009Lahir1 Juli 1980 (umur 44)East Cleveland, Ohio, Amerika SerikatAlmamaterUniversitas BrandeisPekerjaanPelawakMusisiPenulisAktorKota asalSpringfield, Missouri, Amerika Serikat[1]Situs webzachsherwin.com Zach Sherwin (lahir 1 Juli 1980) adalah seorang pelawak, musisi, penulis, dan pemeran asal Amerika Serikat yang dikenal karena menulis dan tampil dalam seri YouTube Epic Rap Battles of History, serta menulis untuk Crazy Ex-Girlfriend di The ...

United States Army post in Alabama Buckner Hall at Fort McClellan in 2014. Fort McClellan, originally Camp McClellan, is a decommissioned United States Army post located adjacent to the city of Anniston, Alabama. During World War II, it was one of the largest U.S. Army installations, training an estimated half-million troops. After the war it became the home of the Military Police Corps, the Chemical Corps and the Women's Army Corps. From 1975 until it was closed in 1999, Fort McClellan was h...






























































![{\displaystyle {\mathcal {O}}_{K_{n}}=\mathbb {Z} \left[\zeta _{n}+\zeta _{n}^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ec8bcba71e05dc82afddc4cd9ba60fb50ed8d01)




