Koch snowflake
| |||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Laut Mirtoa – berita · surat kabar · buku · cendekiawan · JSTOR Laut Mirtoa (Yunani): Πέλαγος Mυρτώο, Myrtöo Pelagos) adalah bagian dari Laut Tengah yang terletak di antara Cyclades dan Pelo...
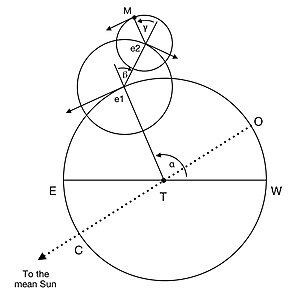
Work by Copernicus De hypothesibus motuum coelestium a se constitutis commentariolus Ms. Austrian National Library, 10530, f. 34rAuthorNicolaus CopernicusLanguageLatinSubjectAstronomyPublication date1514 The Commentariolus (Little Commentary) is Nicolaus Copernicus's brief outline of an early version of his revolutionary heliocentric theory of the universe.[1] After further long development of his theory, Copernicus published the mature version in 1543 in his landmark work, De revolut...
NFL team season 1993 Minnesota Vikings seasonOwnerRoger HeadrickGeneral managerJeff DiamondHead coachDennis GreenHome fieldHubert H. Humphrey MetrodomeResultsRecord9–7Division place2nd NFC CentralPlayoff finishLost Wild Card Playoffs(at Giants) 10–17Uniform ← 1992 Vikings seasons 1994 → The 1993 season was the Minnesota Vikings' 33rd in the National Football League (NFL). The Vikings failed to match their 11–5 record from the previous season, finishing at 9–...

Pour les articles homonymes, voir Parti unioniste. Parti unionisteUnionist Party Présentation Chef Robert Laird BordenArthur Meighen Fondation 1917 Disparition 1920 Fusionné dans Parti national libéral et conservateur Composé de Parti conservateur et libéraux-unionistes Représentation Élections de 1917 153 / 235 modifier Le Parti unioniste est un parti politique canadien formé en 1917 par les députés qui appuient le gouvernement d'unité nationale du premier minis...

Pour les articles homonymes, voir Trnava (homonymie). Trnava Héraldique Drapeau Trnava Rue M.S.Trnavský Administration Pays Slovaquie Région Trnava District Trnava Statut Capitale régionale Primator (maire) Mandat Peter Bročka (Indépendant) mandat : 2018-2022 Code postal 917 01 Plaqueminéralogique TT Code LAU 2 506745 Démographie Gentilé Trnaviens Population 65 207 hab. (31 déc. 2018) Densité 912 hab./km2 Géographie Coordonnées 48° 22′ 41″ ...

Disambiguazione – Se stai cercando altri significati, vedi Carrion (disambigua). CarrionCarrion (a destra) con Shriek contro l'Uomo Ragno, disegni da Bagley/Emberlin UniversoUniverso Marvel Lingua orig.Inglese AutoriBill Mantlo Jim Mooney Frank Springer EditoreMarvel Comics 1ª app.dicembre 1978 1ª app. inSpectacular Spider-Man n. 25 Caratteristiche immaginarieAlter ego Miles Warren (clone) Malcolm McBride William Allen SessoMaschio Poteri levitazione telepatia controllo dell...
此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Part of a series onDiscrimination Forms Institutional Structural Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / Ethnicity Skin color Scientific racism Rank Sex Sexual orientation Species Size Viewpoint Social Arophobia Acephobia Adultism Anti-albinism Anti-autism Anti-homelessness Anti-drug addicts Anti-intellectualism Anti-intersex Anti-left handedness Anti-Masonry Antisemitism Aporophobia Audism Biphobia Clannism Cro...

2002 film CarnageFilm posterDirected byDelphine GleizeWritten byDelphine GleizeProduced byAntonio BazagaDenis DelcampeJérôme DopfferStarringChiara MastroianniCinematographyCrystel FournierEdited byFrançois QuiqueréMusic byÉric Neveux Jérôme RebotierDavid HadjadjDistributed byDiaphana FilmsRelease dates 17 May 2002 (2002-05-17) (Cannes) 13 November 2002 (2002-11-13) (France) Running time130 minutesCountryFranceLanguageFrenchBudget€3.4 million[...

NBC affiliate in Marquette, Michigan WLUC-TVMarquette, MichiganUnited StatesChannelsDigital: 35 (UHF)Virtual: 6BrandingTV6Fox UP (on DT2)ProgrammingAffiliations6.1: NBC6.2: Foxfor others, see § SubchannelsOwnershipOwnerGray Television(Gray Television Licensee, LLC)HistoryFirst air dateApril 28, 1956 (68 years ago) (1956-04-28)Former call signsWDMJ-TV (1956–1964)Former channel number(s)Analog: 6 (VHF, 1956–2009)Former affiliationsCBS (1956–1992)ABC (secondary 1956–1...

Titan Maximumserie TV d'animazione Lingua orig.inglese PaeseStati Uniti AutoreTom Root, Matthew Senreich RegiaChris McKay MusicheShawn Patterson StudioShadowMachine Films, Stoopid Buddy Stoodios, Tom Is Awesome, Williams Street EditoreMatt Mariska ReteAdult Swim 1ª TV27 settembre – 22 novembre 2009 Episodi9 (completa) Durata ep.11 min Generecommedia nera, parodia Titan Maximum è una serie televisiva animata statunitense del 2009, cre...

Internet merupakan salah satu faktor terjadinya banjir informasi Banjir informasi atau kejenuhan informasi adalah suatu keadaan saat pengolahan informasi manusia telah berada di luar kapasitas kemampuan yang sesungguhnya.[1] Frasa ini (dalam bahasa Inggris: information overload) disebutkan dalam buku The Managing of Organizations karya Bertram Gross pada tahun 1964.[2] Dalam era globalisasi, semakin banyak orang terkoneksi dengan internet untuk melakukan penelitiannya sendiri ...

The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: No Tofu – news · newspapers · books · scholar · JSTOR (May 2014) (Learn how...

Penyuntingan Artikel oleh pengguna baru atau anonim untuk saat ini tidak diizinkan.Lihat kebijakan pelindungan dan log pelindungan untuk informasi selengkapnya. Jika Anda tidak dapat menyunting Artikel ini dan Anda ingin melakukannya, Anda dapat memohon permintaan penyuntingan, diskusikan perubahan yang ingin dilakukan di halaman pembicaraan, memohon untuk melepaskan pelindungan, masuk, atau buatlah sebuah akun. Ratu Elizabeth II dari Britania RayaKepala PersemakmuranPotret resmi, 1959Ratu Br...

Casa MilàLa PedreraCasa MilàInformasi umumAlamat92, Passeig de GràciaKotaBarcelona, CatalunyaNegaraSpanyol Casa Milà atau dikenal sebagai La Pedrera adalah sebuah bangunan modernis di Barcelona, Catalonia, Spanyol. Itu adalah kediaman pribadi terakhir yang dirancang oleh arsitek Antoni Gaudi dan dibangun antara tahun 1906 dan 1912. Bangunan ini ditugaskan pada tahun 1906 oleh Pere Milà dan istrinya Roser Segimon. Pada saat itu kontroversial karena fasad batu bergelombang, memutar balkon ...

Questa pagina sull'argomento cronologia sembra trattare argomenti unificabili alla pagina Calendario luni-solare hindu. Commento: Sembra che parlino della stessa cosa Puoi contribuire unendo i contenuti in una pagina unica. Segui i suggerimenti del progetto di riferimento. Una pagina del calendario induista 1871-72 Il calendario induista era il calendario usato in India in epoca vedica, che dopo molti cambiamenti e modifiche a seconda delle diverse regioni si è suddiviso nei moderni ca...

SalamanderRentang fosil: Jura - Kini Salamander totol, Ambystoma maculatum Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Amphibia Ordo: UrodelaScopoli, 1777 Subordo beserta famili Cryptobranchoidea Cryptobranchidae Hynobiidae Salamandroidea Ambystomatidae Amphiumidae Plethodontidae Proteidae Rhyacotritonidae Salamandridae Sirenoidea Sirenidae Habitat salamander (hijau) Salamander atau semandar adalah nama umum bagi sekitar 550 spesies amfibi.[1] Mereka secara umum dici...

人的成長與發展 階段 受精卵 胚胎 胚胎發育 胎兒 嬰兒 幼兒 儿童早期 儿童 前青少年期 青少年 青壯年 中年 老年 生命歷程 人类受精 分娩 爬行學步(英语:Gross motor skill#Learning to walk) 语言习得 青春期 更年期 老化 临终 回光返照 死亡 发展心理学 產前與產後(英语:Prenatal and perinatal psychology) 新生兒與兒童 青少年 青年(英语:Positive Youth Development) 青壯年 成人(英语�...

1014 battle between the Kingdom of Ireland and an Irish-Norse alliance Battle of ClontarfPart of the Viking Invasions of IrelandBattle of Clontarf, oil on canvas painting by Hugh Frazer, 1826Date23 April 1014[1]LocationClontarf, Dublin53°21′54″N 06°11′51″W / 53.36500°N 6.19750°W / 53.36500; -6.19750Result Irish victory Viking power in Ireland broken Death of Brian BoruBelligerents Forces of the High King of Ireland Kingdom of DublinKingdom of Leinst...

Student nation of Uppsala University Norrland's NationUppsala University LocationVästra Ågatan 14 753 11 UppsalaSwedenLatin nameNatio NorlandicaEstablished1646; 378 years ago (1646)InspektorTobias SjöblomMembershipapprox. 8000Websitewww.norrlandsnation.se You can help expand this article with text translated from the corresponding article in Swedish. (December 2009) Click [show] for important tran...


































































