Indefinite sum
|
Read other articles:

Interleukin 12 Interleukin 12, IL-12 adalah sejenis sitokin yang biasanya disekresi oleh DC,[1] MAC dan sel B limfoblastoid (NC-37), sebagai respon terhadap stimulasi antigen. IL-12 disebut juga sebagai faktor stimulan sel T, karena berperan dalam diferensiasi sel T CD4 menjadi sel TH1. Sel T efektor yang memproduksi IL-12 disebut sel T CD30. IL-12 juga stimulan bagi sitokin IFN-γ dan TNF-α. Stimulasi IFN-γ dilakukan dengan mengurangi efek sitokin IL-4 yang menjadi regulator IFN-γ...

Terdapat banyak hal yang menyebabkan kematian ikan secara massal, namun kekurangan oksigen menjadi penyebab yang paling umum Kebinasaan ikan atau kematian ikan massal adalah gejala kematian populasi ikan dan hewan laut pada umumnya secara lokal.[1][2] Penyebab utama adalah berkurangnya oksigen di dalam air, yang dapat terjadi karena berbagai hal seperti kekeringan, ledakan alga, populasi berlebih, atau peningkatan temperatur air. Penyakit dan parasit ikan juga mampu menyebabka...

Badai salju Badai salju terjadi saat udara yang hangat dan basah bertemu dengan udara yang dingin. Massa udara yang hangat dan basah dan massa udara yang dingin tersebut dapat mencapai diameter 1000 km atau lebih. Badai salju yang memengaruhi Amerika Serikat Timur Laut sering mendapatkan uap air dari udara yang berpindah ke utara dari Teluk Meksiko dan udara yang dingin dari massa udara yang datang dari Arktik. Di Amerika Serikat Barat Laut, udara yang hangat dan basah dari Samudera Pasifik m...

Radio station in Galena, IllinoisWDBQ-FMGalena, IllinoisBroadcast areaDubuque, Iowa and VicinityFrequency107.5 MHzBrandingQ107.5ProgrammingFormatClassic hitsAffiliationsCompass Media NetworksPremiere NetworksWestwood OneOwnershipOwnerTownsquare Media(Townsquare License, LLC)Sister stationsKLYV, KXGE, WDBQ, WJODHistoryFirst air date1989 (1989) (as WJOD)Former call signsWJOD (1988-1999)Call sign meaningDubuqueTechnical information[1]Licensing authorityFCCFacility ID30617ClassAERP6,...
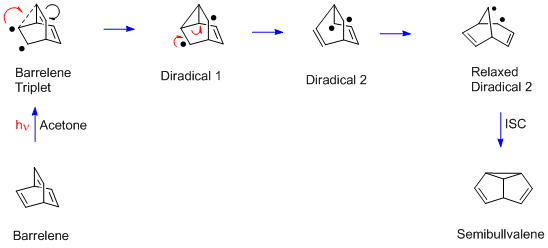
Not to be confused with Vinylcyclopropane rearrangement. In organic chemistry, the di-π-methane rearrangement is the photochemical rearrangement of a molecule that contains two π-systems separated by a saturated carbon atom. In the aliphatic case, this molecules is a 1,4-diene; in the aromatic case, an allyl-substituted arene. The reaction forms (respectively) an ene- or aryl-substituted cyclopropane. Formally, it amounts to a 1,2 shift of one ene group (in the diene) or the aryl group (in ...

Subspecies of honey bee Apis mellifera mellifera Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Hymenoptera Family: Apidae Genus: Apis Species: A. mellifera Subspecies: A. m. mellifera Trinomial name Apis mellifera melliferaLinnaeus, 1758[1] Synonyms[2] Apis mellifica germanica (Pollmann 1879) Apis mellifica nigrita (Lucas 1882) Apis mellifica mellifica variety lehzeni (Buttel-Reepen 1906) Apis mellifica mellifi...

Jamur tiram Jamur tiram Status konservasi Status konservasi: Aman Klasifikasi ilmiah Kerajaan: Fungi Kelas: Homobasidiomycetes Ordo: Agaricales Famili: Tricholomataceae Genus: Pleurotus Spesies: P. ostreatus Nama binomial Pleurotus ostreatusChamp. Jura. Vosg. 1: 112, 1872 Pleurotus ostreatusfloat Karakteristik mikologiHimenium berbentuk insangTudung serongHimenium melanjutTangkai gundulJejak spora berwarna putihJenis ekologi saprotrofEdibilitas: pilihan Jamur tiram di permukaan batang k...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada September 2015. Arkeologi publik adalah laku arkeologi yang kiblatnya adalah arkeologi untuk masyarakat (Noerwidi. 2006). Latar Belakang Istilah Arkeologi Publik muncul pada di Amerika pada tahun 1972 yang dipopulerkan oleh McGimsey melalui tulisannya. Pada masa itu...

University of Virginia basketball court John Paul Jones ArenaLocation295 Massie RoadCharlottesville, Virginia 22903Coordinates38°02′46″N 78°30′25″W / 38.046°N 78.507°W / 38.046; -78.507OwnerUniversity of VirginiaOperatorASM GlobalCapacityBasketball: 14,623[1] Concerts:*End stage 180°: 12,467*End stage 270°: 14,075*End stage 360°: 15,177*Center stage: 15,405*Theatre: 7,352 [2]Record attendance15,219[3](11/12/06 vs. Arizona)Construc...

Cattedrale di San LorenzoFacciataStato Italia RegioneToscana LocalitàGrosseto Coordinate42°45′36.03″N 11°06′49.35″E42°45′36.03″N, 11°06′49.35″E Religionecattolica di rito romano TitolareSan Lorenzo Diocesi Grosseto ArchitettoSozzo Rustichini Stile architettonicoromanico, gotico Inizio costruzione1294 Completamento1302 Modifica dati su Wikidata · Manuale La cattedrale di San Lorenzo è il luogo di culto cattolico più importante della città di Grosseto, chiesa ...

Printing technique This article is about a printing method. For rock types, see Lithology. For the microfabrication process, see microlithography. A lithograph of Charles Marion Russell's The Custer Fight (1903), with the range of tones fading toward the edges Part of a series on theHistory of printing TechniquesWoodblock printing200Movable type1040Intaglio (printmaking)1430Printing pressc. 1440Etchingc. 1515Mezzotint1642Relief printing1690Aquatint1772Lithography1796Chromolithogra...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Long Now Foundation – news · newspapers · books · scholar · JSTOR (February 2022) (Learn how and when to remove this message) American nonprofit organization The Long Now FoundationFormationJanuary 4, 1996; 28 years ago (1996-01-04)Type501(c)(3)Tax ID no. 68-0384748Registration no.C1...

Jewish EncyclopediaCopertina dell'edizione del 1901 AutoreIsidore Singer 1ª ed. originale1901 Lingua originaleinglese Modifica dati su Wikidata · Manuale La Jewish Encyclopedia è una enciclopedia anglofona ideata da Isidore Singer e pubblicata per la prima volta tra il 1901 e il 1906 dalla casa editrice Funk and Wagnalls di New York. L'enciclopedia contiene oltre quindicimila articoli in dodici volumi che vertono sulla storia del giudaismo fino a quel periodo.[1] Col trascorre...

لمعانٍ أخرى، طالع اشتباكات محافظة إدلب (توضيح). اشتباكات محافظة إدلب (يونيو 2012–أبريل 2013)جزء من تصعيد 2012–13 في الحرب الأهلية السوريةالحالة التقريبية في محافظة إدلب، منتصف أغسطس 2012التاريخ3 يونيو 2012 – 18 أبريل 2013(10 أشهرٍ و15 يومًا)الموقعمحافظة إدلب، سورياالنتيجةانتصار ج...

För andra betydelser, se Örnsköldsvik (olika betydelser). Örnsköldsvik Tätort · Centralort Bildmontage över ett antal kända platser i Örnsköldsvik. Land Sverige Landskap Ångermanland Län Västernorrlands län Kommun Örnsköldsviks kommun Distrikt Örnsköldsviks distrikt, Arnäs distrikt, Själevads distrikt Höjdläge 18 m ö.h. Koordinater 63°15′56″N 18°40′34″Ö / 63.26556°N 18.67611°Ö / 63.26556; 18.67611 Area -&...

Georgian footballer Jaba Kankava Kankava in 2014Personal informationDate of birth (1986-03-18) 18 March 1986 (age 38)Place of birth Tbilisi, Georgian SSR, Soviet UnionHeight 1.75 m (5 ft 9 in)Position(s) Defensive midfielderSenior career*Years Team Apps (Gls)2003–2004 Dinamo Tbilisi 14 (0)2005 Alania Vladikavkaz 12 (0)2005–2006 Arsenal Kyiv 24 (4)2007–2015 Dnipro Dnipropetrovsk 91 (4)2010–2012 → Kryvbas Kryvyi Rih (loan) 37 (2)2015–2017 Stade Reims 47 (0)2018�...

2011 FIFA Women's World Cup qualificationTournament detailsTeams125 (from 6 confederations)Tournament statisticsTop scorer(s) Adriana Martín (16 goals)← 2007 2015 → International football competition Qualification for the 2011 FIFA Women's World Cup determines which 15 teams join Germany, the hosts of the 2011 tournament, to play for the Women's World Cup. Europe has 5.5 qualifying berths (including the hosts), Asia 3 berths, North and Central America 2.5 berths, Africa 2 b...

Alejandro Landes Echavarría Información personalNacimiento 1980Sao Paulo, BrasilNacionalidad Colombiana y ecuatorianaEducaciónEducado en Universidad Brown Información profesionalOcupación Director de cine, productor, guionista[editar datos en Wikidata] Alejandro Landes Echavarría (São Paulo, 1980) es un director de cine, productor, guionista y periodista colombiano. Es principalmente conocido por dirigir películas en español como Porfirio, un drama colombiano basado en una ...
君主主義 種類世襲君主制 · 選挙君主制 絶対君主制 · 制限君主制 · 立憲君主制 · 非主権君主制(英語版) · 象徴君主制 · 摂政 概念君主君主制王権神授説天命 歴史マグナ・カルタオスマン帝国の勃興名誉革命フランス革命スペイン立憲革命フランス第一帝政フランス第二帝政明治維新天皇制ドイツ帝国の�...

1992 United States House of Representatives election in Vermont ← 1990 November 3, 1992 1994 → Nominee Bernie Sanders Tim Philbin Lewis E. Young Party Independent Republican Democratic Popular vote 162,724 86,901 22,279 Percentage 57.8% 30.9% 7.9% County results Municipality resultsSanders: 30–40% 40–50% 50–60% 60–70% &#...














![{\displaystyle \sum _{x}f(x)=\sum _{k=1}^{\infty }{\binom {x}{k}}\Delta ^{k-1}[f]\left(0\right)+C=\sum _{k=1}^{\infty }{\frac {\Delta ^{k-1}[f](0)}{k!}}(x)_{k}+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6758a97991a0410ddfb47366eb53c4d7597ba5b5)



































































