Ideal solution
|
Read other articles:
Dorothy Johnson Vaughan Dorothy Johnson Vaughan (Kansas City, 20 settembre 1910 – Hampton, 10 novembre 2008) è stata una matematica e programmatrice statunitense afro-americana che ha lavorato per il National Advisory Committee for Aeronautics (NACA) e successivamente per la NASA, al Langley Research Center a Hampton, in Virginia. Prima di entrare al Langley Research Center della NACA nel 1943, Vaughan fu professoressa di matematica alla R. R. Moton High School di Farmville, in Virginia.&#...

Keuskupan Agung GuiyangArchidioecesis Coeiiamensis天主教贵阳总教区LokasiNegara ChinaProvinsi gerejawiGuiyangStatistikLuas100.000 km2 (39.000 sq mi)Populasi- Total- Katolik(per 1950)7.000.00024,713 (0.4%)InformasiRitusRitus LatinKatedralKatedral Santo Yusuf di GuiyangKepemimpinan kiniPausFransiskusUskup agungPaul Xiao Zejiang Keuskupan Agung Guiyang/Kweyang (Latin: Coeiiamen(sis)code: la is deprecated , Hanzi sederhana: 贵阳; Hanzi tradisio...

Nabhaniالنباهنة1154–1624Ibu kotaBahlaBahasa resmiArabAgama Islam IbadiPemerintahanMonarkiMalik (raja) • 1152–1176 Muhammed al-Fallah (pertama)• hingga 1624 Sulaiman bin Sulaiman (terakhir) Sejarah • Didirikan 1154• Dibubarkan 1624 Didahului oleh Digantikan oleh ksrKekaisaran Seljuk Yarubi Sekarang bagian dari Oman Uni Emirat Arab Sunting kotak info • Lihat • BicaraBantuan penggunaan templat ini Wangas Nabhani (Arab: أسرة بن...

فغر المعدة بالمنظار عبر الجلد فغر المعدة بالمنظار عبر الجلد. معلومات عامة من أنواع فغر المعدة تعديل مصدري - تعديل فغر المعدة بالمنظار عبر الجلد (بالإنجليزية: Percutaneous endoscopic gastrostomy) هو إجراء طبي تنظيري يتم فيه تمرير أنبوب (أنبوب فغر المعدة بالمنظار عبر الجلد) إلى معدة �...

The BreadwinnerTeaser posterSutradaraNora TwomeyProduser Angelina Jolie Jordan Peele Anthony Leo Tomm Moore Andrew Rosen Paul Young Mimi Polk Gitlin Ditulis oleh Anita Doron Deborah Ellis BerdasarkanThe Breadwinneroleh Deborah EllisPemeran Saara Chaudry Soma Bhatia Noorin Gulamgaus Laara Sadiq Ali Badshah Shaista Latif Kawa Ada Ali Kazmi Perusahaanproduksi Cartoon Saloon Aircraft Pictures[1] Guru Studio[2] Jolie Pas[3] Irish Film Board[4] Melusine Productions T...
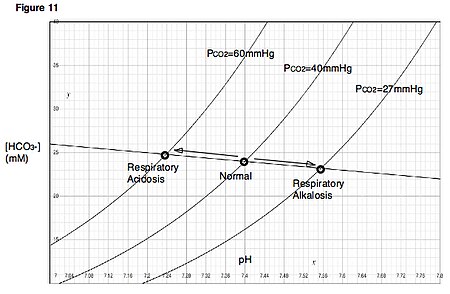
artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Alkalosis respiratorikDavenport diagramInformasi umumSpesialisasiPulmonologi, Kedokteran perawatan intensif, Penyakit dalam Alkalosis respir...

For the current administrative region of Lublin, see Lublin Voivodeship. This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (February 2020) (Learn how and when to remove this message) Lublin District (German: Distrikt Lublin) was one of the first four Nazi districts of the General Governorate region of German-occupied Poland dur...

МифологияРитуально-мифологическийкомплекс Система ценностей Сакральное Миф Мономиф Теория основного мифа Ритуал Обряд Праздник Жречество Мифологическое сознание Магическое мышление Низшая мифология Модель мира Цикличность Сотворение мира Мировое яйцо Мифическое �...

Peta letak Yichang Yichang (Hanzi: 宜昌) merupakan nama kota yang terletak di provinsi Hubei di RRT. Geografi Yichang memiliki luas wilayah 21.084 km². Kota ini terletak di Provinsi Hubei dan bagian timur Jurang Xiling (西陵峡). Kota ini bermuara di Sungai Panjang. Temperatur udara rata-rata di kota ini ialah 16-18 °C. Demografi Kota ini memiliki jumlah penduduk sekitar 3,9 juta. Di daerah kota dihuni 600.000 orang. Kota ini didirikan pada tahun 278. Artikel bertopik geografi...

Laws of Ukraine regarding language Language policy in Ukraine is based on its Constitution, international treaties and on domestic legislation. According to article 10 of the Constitution, Ukrainian is the official language of Ukraine, and the state shall ensure the comprehensive development and functioning of the Ukrainian language in all spheres of social life throughout the entire territory of the country. Some minority languages (such as Russian and Belarusian) have significantly less pro...

Lukisan karya Jan Matejko Untuk penguasa lain yang bernama sama, lihat Ladislaus I. Władysław I Łokietek (yang Pendek) dari Polandia (1260/1261-2 Maret 1333) adalah Raja Polandia yang berkuasa di antara tahun 1320–1333. Ia adalah putra Kazimierz I Kujawski. Setelah ayahandanya meninggal dunia, Władysław mewarisi Kujawy. Menyusul meninggalnya kedua saudaranya, semua warisan jatuh ke tangan Władysław, yang mulai menyatukan kembali Kerajaan Polandia. Pada tahun 1318, Władysław memulai...

Ongoing COVID-19 viral pandemic in Liechtenstein This article needs to be updated. Please help update this article to reflect recent events or newly available information. (December 2020) You can help expand this article with text translated from the corresponding article in German. (February 2021) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point fo...

1940s British turbojet aircraft engine For the 1928 piston engine, see de Havilland Ghost (V8). Ghost A Swedish licensed-built de Havilland Ghost, the RM 2 Type Turbojet Manufacturer de Havilland Engine Company First run 2 September 1945 Major applications de Havilland Comet de Havilland Venom de Havilland Sea Venom Developed from de Havilland Goblin The de Havilland Ghost (originally Halford H-2) was the de Havilland Engine Company's second design of a turbojet engine to enter production and...

Esoteric Buddhism found in Maritime Southeast Asia Part of a series onVajrayana Buddhism TraditionsHistorical traditions: Ari-Acharya Burmese-Bengal † Yunnan Indonesian Esoteric Buddhism † Filipino Esoteric Buddhism † East Asian Chinese Japanese Nepalese Inner Asian Tibetan Altaic (o, x, b, t, k, y) New branches: Gateway of the Hidden Flower New Kadampa Buddhism Shambhala Buddhism True Awakening Tradition History Tantrism Mahasiddha Sahaja Pursuit Buddhahood Bodhisattva Kalachakra Pract...

Cet article est une ébauche concernant la science-fiction. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Space Western Comics, bande dessinée mélangeant western et science fiction (1952). Le space western est un sous-genre de la science-fiction qui combine des éléments issus du western à ceux caractérisant le genre SF. Cela peut aller d'une simple influence du western sur le genre en question, comme la ...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Moderación» – noticias · libros · académico · imágenesEste aviso fue puesto el 13 de abril de 2012. La moderación es evitar llegar a un punto muerto o a los extremos, en busca de equilibrio. La moderación como virtud es entendida como una virtud, la moderación es equivalente a la mesura y la prudencia. La moderación es el evitar llegar a un punto muert...

سيليكا نباتية من شجرة Paulownia fargesii. سيليكا النبات [1] (يقابلها باللغة الإنجليزية كلمة Phytolith، وهي مشتقة من الإغريقية بمعنى «صخر النبات».) هي بنى مجهرية (مكروئية) صلبة مؤلفة من السيليكا والموجودة في أنسجة بعض النباتات، وهي لا تتفكك مع تحلل النباتات. تتشكل هذه السيليكا النباتي...

Economic concept The marginal efficiency of capital (MEC) is that rate of discount which would equate the price of a fixed capital asset with its present discounted value of expected income. The term “marginal efficiency of capital” was introduced by John Maynard Keynes in his General Theory, and defined as “the rate of discount which would make the present value of the series of annuities given by the returns expected from the capital asset during its life just equal its supply price�...

ما تشونغ-يينغ (بالصينية التقليدية: 馬仲英) ما تشونغ يينغ معلومات شخصية الميلاد سنة 1910 مقاطعة لينشيا، إقليم قانسو الوفاة سنة 1936 (25–26 سنة) مواطنة سلالة تشينغ الحاكمة جمهورية الصين اللقب غا سو-لينغ (الجنرال الطفل أو القائد الصغير)[1] أو الحصان الكبير[2] ا...

Disambiguazione – Se stai cercando altri significati, vedi Sannio (disambigua). SannioSannio - LocalizzazioneL'antico Samnium secondo l'Historical Atlas di William R. Shepherd (1911) Dati amministrativiNome completo(LA) Samnium; Samnitium ager[1] Nome ufficialeSafinim[2] Lingue parlateosco, in seguito latino PoliticaNascitaVI secolo a.C. Causainsediamento dell'area da parte dei Sanniti FineI secolo a.C. Causaromanizzazione dell'area ed istituzione delle XI regiones augu...










































![{\displaystyle x_{i}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a32830173af0dc0eaf16f580cc75ef2f78b4f15e)








