Graph factorization
|
Read other articles:

Go OverAlbum studio karya High and Mighty ColorDirilis14 September 2005Direkam2005GenrePopDurasi45:16LabelSME RecordsKronologi High and Mighty Color Go Over(2005) Gou on Progressive(2006)Gou on Progressive2006 Go Over adalah album pertama High and Mighty Color yang dirilis pada tanggal 14 September 2005. Album ini meraih posisi nomor 8 di tangga lagu Oricon dan bertahan di tangga lagu selama 7 minggu. Lagu G∞VER – 2:25 NOTICE – 4:11 PRIDE – 4:18 Naked – 3:33 OVER – 4:05 Days �...

Kapuk MuaraKelurahanNegara IndonesiaProvinsiDaerah Khusus Ibukota JakartaKota AdministrasiJakarta UtaraKecamatanPenjaringanKode Kemendagri31.72.01.1003 Kode BPS3175010002 Luas10,055 km2Jumlah penduduk38.937 jiwaKepadatan1.300,46 jiwa/km2 Posisi Kelurahan Kapuk Muara di Kecamatan Penjaringan, Jakarta Utara Kelurahan Kapuk Muara, Penjaringan memiliki kode pos 14460 Kelurahan ini terletak di kecamatan Penjaringan, Jakarta Utara. Kelurahan ini memiliki penduduk sebesar 38.937 jiwa dan luas 1...
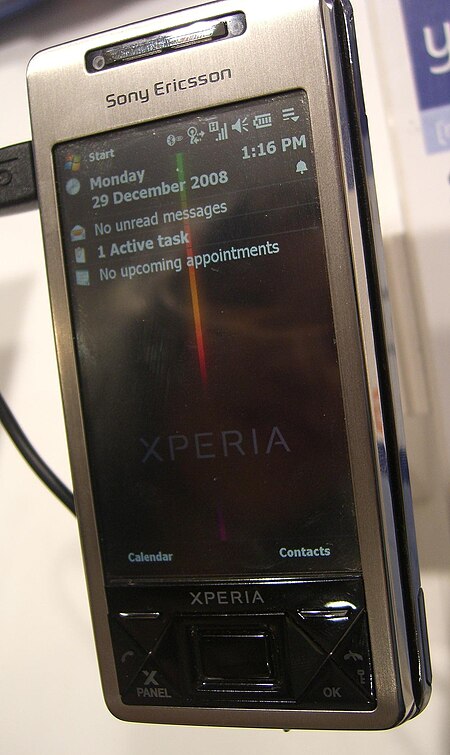
Sony XperiaPembuatSony MobileJenisPonsel cerdas, tablet, phabletTanggal rilis27 Oktober 2008; 15 tahun lalu (2008-10-27)Sistem operasiAndroid (sejak tahun 2010)Windows Mobile (2008–2010)MasukanLayar sentuh Xperia (/ɛkˈspɪəriə/) adalah sebuah merek ponsel cerdas dan tablet milik Sony Mobile. Nama Xperia berasal dari kata experience, dan pertama kali digunakan pada tagline Xperia X1, yakni I Xperia the best. Sony Mobile sebelumnya dikenal secara global dengan nama Sony Ericsson, dan...

American college basketball season 2023–24 Illinois Fighting Illini men's basketballBig Ten tournament championsNCAA tournament, Elite EightConferenceBig Ten ConferenceRankingCoachesNo. 7APNo. 6Record29–9 (14–6 Big Ten)Head coachBrad Underwood (7th season)Assistant coaches Chester Frazier (3rd season) Tim Anderson (3rd season) Geoff Alexander (3rd season) Zach Hamer (1st season) Tyler Underwood (1st season) Home arenaState Farm CenterSeasons← 2022–232024...

Air Saint-Pierre Codes IATAOACIIndicatif d'appel PJ SPM Saint-Pierre Repères historiques Date de création 1964 Généralités Basée à Aéroport de Saint-Pierre Pointe-Blanche Taille de la flotte 3 (Cessna F406, ATR 42-500, ATR 42-600)[1] Nombre de destinations 7 Siège social Saint-Pierre, France Dirigeants Benoit Olano, président Site web www.airsaintpierre.com modifier Air Saint-Pierre (code AITA : PJ ; code OACI : SPM) est une compagnie aérienne française, basée à ...

Gentle politeness and courtly manners Courtly redirects here. For court culture in medieval to early modern Europe, see Courtly love and Royal court. Not to be confused with Etiquette. Courtesy (from the word courteis, from the 12th century) is gentle politeness and courtly manners. In the Middle Ages in Europe, the behaviour expected of the nobility was compiled in courtesy books. History The apex of European courtly culture was reached in the Late Middle Ages and the Baroque period (i.e. ro...

News programmes on British ITV network ITV NewsLogo used since 2013Company typeTelevision newsGenreNational and international newsFounded22 September 1955 (1955-09-22) (as ITN)FounderIndependent Television AuthorityHeadquartersLondon, EnglandArea servedUnited KingdomKey peopleMichael Jermey(ITV Director of News & Current Affairs)Guy Phillips(Editor, ITV News regions)Rachel Corp[1](Editor)ParentITN, ITV plcDivisionsITV Regional NewsWebsiteitv.com/news ITV News is the...

Hong Kong Canadian actress Not to be confused with G.E.M., also known as Gloria Tang. In this Chinese name, the family name is Tang.Gloria Tang Pui-yee鄧佩儀Tang in 2019Born (1992-11-10) 10 November 1992 (age 31)British Hong KongCitizenshipCanadaOccupation(s)Actress, television hostYears active2013–presentTitle Miss Chinese Vancouver 2012 Miss Chinese International 2013 Chinese nameTraditional Chinese鄧佩儀Simplified Chinese邓佩仪TranscriptionsStandard MandarinHanyu ...

Term used by Orthodox Jewish groups to describe their JudaismThis article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Torah Judaism – news · newspapers · books �...

Disambiguazione – Se stai cercando l'antica strada romana Tiberina, vedi Via Tiberina. Strada statale 3 bisTiberinaLocalizzazioneStato Italia Regioni Umbria Toscana Emilia-Romagna Province Terni Perugia Arezzo Forlì-Cesena Ravenna DatiClassificazioneStrada statale InizioTerni FineRavenna Lunghezza250,565 km Provvedimento di istituzioneR.D.L. 5 settembre 1938, n. 1594[1] GestoreANAS PercorsoStrade europee · · Manuale La stra...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أغسطس 2021) ما زال مصدر الميثان على المريخ غير معلوم، ويظهر رصده في هذه الصورة. عتبر وجود الميثان في الغلاف الجوي للمريخ محل اهتمام للعديد من الجيولوجيين وعلماء الأحياء ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Juni 2012. Minjuhwa adalah sebuah kata sindiran yang digunakan untuk menyebut kata demokrasi di Korea Selatan. Kata ini diciptakan secara anonim pada tahun 1991 untuk menyindir partai politik oposisi yang suka menekan suara minoritas. Artikel bertopik Korea ini adal...

Las amenazas pueden ser sutiles o abiertas. Actor Justus D. Barnes, en Asalto y robo de un tren Las amenazas son un delito o una falta, consistente en el anuncio de un mal futuro ilícito que es posible, impuesto y determinado con la finalidad de causar inquietud o miedo en el amenazado. Las amenazas deben ser creíbles y, además, pueden consistir en amenazar con un mal ilícito que, por su parte, puede ser o no constitutivo de delito. Definición El mal ha de ser posible, en el sentido de q...

Sports season2019–20 CEV Champions LeagueLeagueCEV Champions LeagueSportVolleyballDurationQualifying round: 22 October – 27 November 2019 Main tournament: 3 December 2019 – 11 March 2020Number of teams28 (10 qual. + 18 main tourn.)CEV Champions League seasons← 2018–192020–21 → The 2020–21 CEV Champions League was the 61st edition of the highest level European volleyball club competition organised by the European Volleyball Confederation. The tournament has been cance...

Overview of the use of capital punishment in Belarus Europe holds the greatest concentration of abolitionist states (blue). Map current as of 2021 Abolished for all offences Retains death penalty Legal form of punishment but has had a moratorium for at least ten years Capital punishment is a legal penalty in Belarus. At least one execution was carried out in the country in 2022.[1] Also known as an Exceptional Measure of Punishment (Russian: Иск�...

Language isolate of southern Louisiana, US ChitimachaSitimaxaČitimaašaPronunciation[t͡ʃitimaːʃa]Native toUSARegionSouthern LouisianaEthnicityChitimachaExtinct1940[1]with the death of Delphine Ducloux[2]RevivalIn progress, language learned by children through immersion program[3]Language familyLanguage isolateLanguage codesISO 639-3ctmGlottologchit1248ELPChitimachaDistribution of Chitimacha language Chitimacha (/ˌtʃɪtɪməˈʃɑː/ CHIT-i-mə-SHAH&...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Randall Duk Kim – berita · surat kabar ...

Head of the British Civil Service This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cabinet Secretary United Kingdom – news · newspapers · books · scholar · JSTOR (February 2013) (Learn how and when to remove this message) Cabinet SecretaryRoyal Arms as used by His Majesty's GovernmentIncumbentSimon Case ...

Island of Labuan, Malaysia Daat IslandNative name: Pulau DaatGeographyLocationLabuan, MalaysiaCoordinates5°16′25.0″N 115°19′05.1″E / 5.273611°N 115.318083°E / 5.273611; 115.318083Total islands1Area2.4 km2 (0.93 sq mi) The Daat Island (Malay: Pulau Daat) is an island in Labuan, Malaysia. History In 1856, Labuan Governor George Warren Edwardes issued a grant to John Gavaron Treacher and Clarence Cooper to be the owner of the island. Since then,...

Voce principale: Associazione Calcio Reggiana 1919. AC Reggiana 1919Stagione 2023-2024Sport calcio Squadra Reggiana Allenatore Alessandro Nesta All. in seconda Lorenzo Rubinacci Presidente Carmelo Salerno Serie B11º Coppa ItaliaSedicesimi Maggiori presenzeCampionato: Portanova (36)Totale: Portanova (39) Miglior marcatoreCampionato: Gondo (6)Totale: Portanova (7) StadioMapei Stadium - Città del Tricolore (23 717) Abbonati6.698[1] Maggior numero di spettatori16.121 vs Parma...


