General Leibniz rule
|
Read other articles:

Street in Bremen, Germany Helenenstraße Street in Bremen, GermanyHelenenstraße in 2014Former name(s)FrankenstraßeLocationStone Gate district, Bremen, GermanyCoordinates53°04′20″N 8°49′35″E / 53.072222°N 8.826389°E / 53.072222; 8.826389FromVor dem SteintorOtherKnown forProstitution The Helenenstraße is a street in the Steintor locality in the eastern suburbs of Bremen, Germany. The street was built in the 19th century and is known for prostitution. Const...

Leonid Krasin Komisar Rakyat untuk Perdagangan Luar NegeriMasa jabatan6 Juli 1923 – 18 November 1925 PenggantiAlexander TsiurupaKomisar Rakyat untuk Perdagangan dan IndustriMasa jabatanNovember 1918 – Juni 1920Komisar Rakyat untuk TransportasiMasa jabatanMaret 1919 – Desember 1920 Informasi pribadiLahir(1870-07-15)15 Juli 1870Kurgan, Kegubernuran Tobolsk, Kekaisaran RusiaMeninggal24 November 1926(1926-11-24) (umur 56)London, Britania RayaKewarganegaraanSo...

R. Sidharta Wisnu Graha Gubernur Akademi MiliterPetahanaMulai menjabat 17 Juli 2023 PendahuluErwin DjatnikoPenggantiPetahanaKepala Staf Komando Daerah Militer XVII/CenderawasihMasa jabatan6 Desember 2021 – 17 Juli 2023 PendahuluBambang TrisnohadiPenggantiYudha Medy Dharma ZafrulKomandan Korem 051/WijayakartaMasa jabatan9 April 2020 – 6 Desember 2021 PendahuluSusiloPenggantiYustinus Nono YuliantoInspektur Komando Daerah Militer I/Bukit BarisanMasa jabatan2018 –...

Children's television series The Puzzle PlaceCreated byCecily TruettSuzanne SingerRob StorkEllis WeinerDavid YazbekStarringAlice DinneanCarmen OsbahrJim MartinNoel MacNealEric JacobsonPeter LinzMatt VogelDrew MasseyAlison MorkStephanie D'AbruzzoTerri HardinAllan TrautmanTheme music composerSteve HorelickJanet WeirComposersSteve HorelickJanet WeirCountry of originUnited StatesOriginal languageEnglishNo. of seasons3No. of episodes75ProductionExecutive producersCecily TruettLarry LancitStephen K...

Thai diplomatic missions This is a list of diplomatic missions of Thailand, excluding honorary consulates. Current missions Africa Host country Host city Mission Concurrent accreditation Ref. Egypt Cairo Embassy Countries: Djibouti Eritrea Sudan [1][2] Kenya Nairobi Embassy Countries: Burundi Comoros Congo-Kinshasa Ethiopia Rwanda Seychelles Somalia South Sudan Tanzania Uganda Internatio...

The United Nations Educational, Scientific and Cultural Organization (UNESCO) World Heritage Sites are places of importance to cultural or natural heritage as described in the UNESCO World Heritage Convention, established in 1972.[1] Haiti accepted the convention on January 18, 1980, making its historical sites eligible for inclusion on the list. As of 2023, Haiti has only one World Heritage Site, National History Park – Citadel, Sans Souci, Ramiers, which was inscribed in 1982. &#...

Vietnamese-American poker player (born 1967) Minh LyMinh Ly at the 2005 World Series of PokerResidenceTemple City, CaliforniaBorn (1967-03-24) March 24, 1967 (age 57)World Series of PokerBracelet(s)NoneMoney finish(es)13Highest ITMMain Event finish9th, 2002World Poker TourTitle(s)1Final table(s)1Money finish(es)2Information accurate as of 12 September 2009. Minh Hoang Ly (born March 24, 1967, in Vietnam)[1] is a Vietnamese-American professional poker player based in Temple City, ...

Apriastini Bakti BugiansriSaat menjabat sebagai Kapusjarah Polri Informasi pribadiLahir1 April 1964 (umur 60)IndonesiaAlma materSekolah Polisi Wanita (1984)Sekolah Pembentukan Perwira (1993)PekerjaanPolisiKarier militerPihak IndonesiaDinas/cabang Kepolisian Negara Republik IndonesiaMasa dinas1984–2022Pangkat Inspektur Jenderal PolisiSatuanSDMSunting kotak info • L • B Irjen. Pol. (Purn.) Apriastini Bakti Bugiansri, S.I.K. (lahir 1 April 1964)[1] adalah s...

Reruntuhan Tikal, yang sebelumnya merupakan salah satu kota terkuat pada masa Maya Klasik. Keruntuhan Maya Klasik merujuk pada kemunduran peradaban Maya Klasik dan ditinggalkannya kota-kota Maya Klasik di dataran rendah Maya selatan antara abad ke-8 hingga abad ke-9. Peristiwa ini tidak sama dengan keruntuhan Maya Praklasik pada abad ke-2. Periode Klasik dalam kronologi Mesoamerika secara umum merujuk pada periode antara tahun 300 hingga 900, dengan seratus tahun terakhir (800-900) disebut Kl...

Latin Catholic diocese in the Philippines This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Roman Catholic Diocese of Malolos – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this message) Diocese of MalolosDioecesis MalolosinaeDiyosesis ng MalolosDiócesis de MalolosCa...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (نوفمبر 2023) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...
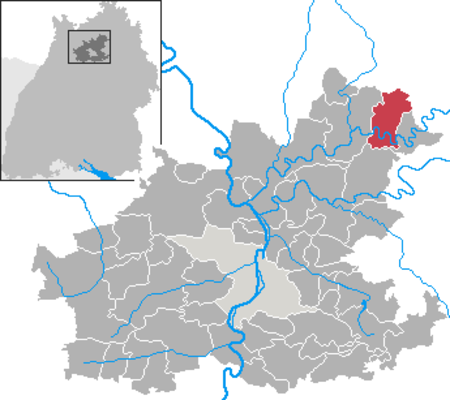
Widdern Lambang kebesaranLetak Widdern di Heilbronn NegaraJermanNegara bagianBaden-WürttembergWilayahStuttgartKreisHeilbronnSubdivisions2Pemerintahan • MayorMichael F. ReinertLuas • Total25,23 km2 (974 sq mi)Ketinggian185 m (607 ft)Populasi (2021-12-31)[1] • Total1.836 • Kepadatan0,73/km2 (1,9/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos74259Kode area telepon06298Pelat kendaraanHNSitus webwww.widdern.d...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (February 2016) (Learn how and when to remove this message) This article needs additional citations for verification. Please help improve this article by adding citations to relia...

انقلاب 2022 في بوركينا فاسو جزء من تمرد الجهاديين في بوركينا فاسو جنود بوركينا فاسو يقومون بدوريات في شوارع واغادوغو في اليوم التالي للانقلاب معلومات عامة التاريخ 23 - 24 يناير 2022 البلد بوركينا فاسو تسببت في اعتقال، وحل [لغات أخرى]، وتأسيس [لغات �...

Brad Gilbert Medallista olímpico Brad GilbertPaís Estados UnidosResidencia San Rafael (California)Fecha de nacimiento 9 de agosto de 1961 (63 años)Lugar de nacimiento Oakland, California, Estados UnidosAltura 1,85 m (6′ 1″)Peso 73 kg (161 lb)Profesional desde 1982Retiro 1995Brazo hábil Diestro; revés a una mano.Dinero ganado 5 507 973 dólares estadounidensesPerfil oficial ATP Perfil ATPIndividualesRécord de su carrera 519–288Títulos de su carrera 2...

إيان كانينغ معلومات شخصية الميلاد 23 يوليو 1979 (45 سنة) برستل الجنسية المملكة المتحدة الحياة العملية المهنة منتج أفلام اللغات الإنجليزية الجوائز جائزة الأوسكار لأفضل فيلم (عن عمل:خطاب الملك) (2009) المواقع IMDB صفحته على IMDB تعديل مصدري - تعديل إيان كا�...

なすからすやまし 那須烏山市 山あげ祭 那須烏山市旗2005年10月1日制定 那須烏山市章2005年10月1日制定 国 日本地方 関東地方都道府県 栃木県市町村コード 09215-1法人番号 7000020092151 面積 174.35km2総人口 22,856人 [編集](推計人口、2024年8月1日)人口密度 131人/km2隣接自治体 さくら市、那須郡那珂川町、塩谷郡高根沢町、芳賀郡市貝町、茂木町茨城県常陸大宮市市の木 けや...

AbadiñoNom officiel (eu) AbadiñoNoms locaux (eu) Abadiño, (es) AbadianoGéographiePays EspagneCommunauté autonome Pays basqueProvince BiscayeComarques DurangaldeaPartie de Communauté de communes du bailliage de Durango (d)Superficie 36,26 km2Altitude 144 mCoordonnées 43° 09′ 09″ N, 2° 36′ 27″ ODémographiePopulation 7 708 hab. (2023)Densité 212,6 hab./km2 (2023)Gentilé AbadiñarFonctionnementStatut Municipalité...

















![{\displaystyle {\begin{aligned}(fg)^{(n+1)}&=\left[\sum _{k=0}^{n}{\binom {n}{k}}f^{(n-k)}g^{(k)}\right]'\\&=\sum _{k=0}^{n}{\binom {n}{k}}f^{(n+1-k)}g^{(k)}+\sum _{k=0}^{n}{\binom {n}{k}}f^{(n-k)}g^{(k+1)}\\&=\sum _{k=0}^{n}{\binom {n}{k}}f^{(n+1-k)}g^{(k)}+\sum _{k=1}^{n+1}{\binom {n}{k-1}}f^{(n+1-k)}g^{(k)}\\&={\binom {n}{0}}f^{(n+1)}g^{(0)}+\sum _{k=1}^{n}{\binom {n}{k}}f^{(n+1-k)}g^{(k)}+\sum _{k=1}^{n}{\binom {n}{k-1}}f^{(n+1-k)}g^{(k)}+{\binom {n}{n}}f^{(0)}g^{(n+1)}\\&={\binom {n+1}{0}}f^{(n+1)}g^{(0)}+\left(\sum _{k=1}^{n}\left[{\binom {n}{k-1}}+{\binom {n}{k}}\right]f^{(n+1-k)}g^{(k)}\right)+{\binom {n+1}{n+1}}f^{(0)}g^{(n+1)}\\&={\binom {n+1}{0}}f^{(n+1)}g^{(0)}+\sum _{k=1}^{n}{\binom {n+1}{k}}f^{(n+1-k)}g^{(k)}+{\binom {n+1}{n+1}}f^{(0)}g^{(n+1)}\\&=\sum _{k=0}^{n+1}{\binom {n+1}{k}}f^{(n+1-k)}g^{(k)}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/195166910864530fea5b647df661b47df305b4b3)




