Decision Linear assumption
|
Read other articles:

Kibboutz Kfar Masaryk. Kibboutz Lotan. Un kibboutz (de l'hébreu : קיבוץ, au pluriel, קיבוצים : kibboutzim, signifiant « assemblée » ou « ensemble ») est un type de village collectiviste créé pour la première fois en 1909 en Palestine alors ottomane. Le premier, Degania Alef (en français : « le bleuet »), fut créé par douze juifs d'origines russe et polonaise adhérant au Bund, un mouvement sioniste d'influence socialiste. ...

Pour les articles homonymes, voir Rubinstein. Ariel RubinsteinAriel Rubinstein en 2007BiographieNaissance 13 avril 1951 (72 ans)JérusalemNationalité israélienneFormation Université hébraïque de JérusalemActivités Économiste, professeur d'universitéAutres informationsA travaillé pour Université de New YorkUniversité de Tel AvivMembre de Société d'économétrie (1985)Academia Europaea (2012)British AcademyAcadémie américaine des arts et des sciencesAcadémie israélienne ...

Keldon Johnson Keldon Johnson con la maglia di Kentucky Nazionalità Stati Uniti Altezza 196 cm Peso 100 kg Pallacanestro Ruolo Ala piccola Squadra San Antonio Spurs Carriera Giovanili Oak Hill Academy2018-2019 Kentucky Wildcats Squadre di club 2019- San Antonio Spurs264 (4.384)2019-2020→ Austin Spurs31 (630) Nazionale 2021 Stati Uniti4 (4) Palmarès Olimpiadi Oro Tokyo 2020 Il simbolo → indica un trasferimento in prestito. Statistiche aggiornate al ...

Aiko Nakamura Nazionalità Giappone Altezza 163 cm Peso 56 kg Tennis Carriera Singolare1 Vittorie/sconfitte 268–237 Titoli vinti Miglior ranking 47º (6 agosto 2007) Risultati nei tornei del Grande Slam Australian Open 3T (2006, 2007) Roland Garros 1T (2005, 2006, 2007, 2008) Wimbledon 2T (2005, 2007) US Open 2T (2005, 2006) Doppio1 Vittorie/sconfitte 80–113 Titoli vinti Miglior ranking 64º (3 marzo 2008) Risultati nei tornei del Grande Slam Australia...

Swiss-born British painter, draughtsman and writer on art (1741–1825) Henry FuseliRAHenry Fuseli, 1778. Portrait by James Northcote.BornJohann Heinrich Füssli(1741-02-07)7 February 1741Zürich, SwitzerlandDied17 April 1825(1825-04-17) (aged 84)Putney Hill, London, EnglandNationalitySwissKnown forPainting, draughtsmanshipNotable workThe NightmareMovementRomanticismSpouse Sophia Rawlins (m. 1788) Henry Fuseli RA (/ˈfjuːzəli, fjuːˈzɛli/ FEW-zə-l...

Bilateral relationsChile–Spain relations Chile Spain Chile–Spain relations are the current and historical relations between Chile and Spain. Both nations are members of the Association of Spanish Language Academies, Organization of Ibero-American States, Organisation for Economic Co-operation and Development and the United Nations. History Spanish conquest Spanish conquistador Pedro de Valdivia founding the city of Santiago Main article: Conquest of Chile In 1536, Spanish explorer Diego d...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...
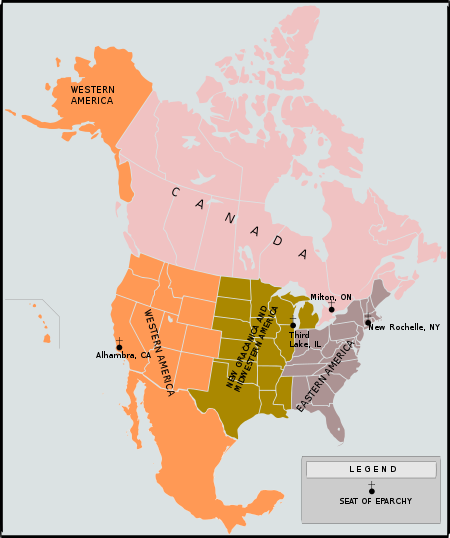
Serbian Orthodox Diocese of Canada redirects here. For other uses, see Diocese of Canada (disambiguation). Serbian Orthodox Eparchy of CanadaThe Holy Transfiguration MonasteryCoat of armsLocationTerritoryCanadaHeadquartersCampbellville, Milton, OntarioCoordinates43°26′04″N 79°57′51″W / 43.434372°N 79.964054°W / 43.434372; -79.964054InformationDenominationEastern OrthodoxSui iuris churchSerbian Orthodox ChurchEstablished1983Cathedral Saint Nicholas Serbian O...

L'industrie des plastiques conçoit, fabrique (plasturgie) et commercialise des matériaux polymères — communément dénommés « plastiques » — utilisés pour de nombreux usages (ex. : emballage, construction, électronique, industrie aérospatiale, transport, agriculture, sylviculture, jouets, gadgets, sans oublier les microplastiques dans certains dentifrices et cosmétiques). Une grande partie de la partie amont (production) de ce secteur est classée dans l...

SMK Negeri 8 Surakarta SMKI Negeri Surakarta KOKAR SurakartaInformasiDidirikan27 Agustus 1950JenisNegeriAkreditasiA[1]Nomor Statistik Sekolah781036104001Nomor Pokok Sekolah Nasional20328154Kepala SekolahWening Sukmanawati, S.Pd., M.PdJumlah kelas85[2]Jurusan atau peminatanSeni pertunjukan: Seni Karawitan Penataan Karawitan Seni Tari Penataan Tari Seni Pedalangan Seni Musik Populer Seni Teater Desain Komunikasi Visual: Multimedia Broadcasting dan perfilman: Produksi d...

Census-designated place in Maryland, United StatesBethesda, MarylandCensus-designated placeFrom top: Bethesda Meeting House, Bethesda's Madonna of the Trail statue, the National Institutes of Health, downtown Bethesda near the Bethesda Metro station, Bethesda Avenue at night, Bethesda Theatre, and the Connie Morella Library.Boundaries of Bethesda CDP from U.S. Census BureauLocation of Bethesda in Montgomery County, MarylandCoordinates: 38°59′5″N 77°6′47″W / 38.98472...

Part of a series on: Kurdish history and Kurdish culture People List of Kurds Population Homeland Kurdistan Turkey (Northern Kurdistan) Iran (Eastern Kurdistan) Iraq (Southern Kurdistan) Syria (Western Kurdistan) Diaspora Armenia Australia Azerbaijan Belgium Canada Czech Republic Denmark Finland France Georgia Germany Greece Iraq Iran Ireland Israel Japan Jordan Kazakhstan Lebanon Netherlands New Zealand Norway Palestine Pakistan Romania Russia Syria Sweden Turkmenistan Turkey Ukraine ...

Medardo Rosso al lavoro nel suo studio Medardo Rosso (Torino, 21 giugno 1858 – Milano, 31 marzo 1928) è stato uno scultore italiano, principale esponente dell'impressionismo in scultura. Indice 1 Biografia 2 Rosso e i bambini 3 Opere 4 Scritti di Medardo Rosso 5 Note 6 Bibliografia 7 Altri progetti 8 Collegamenti esterni Biografia Medardo Rosso nacque nel 1858 a Torino, dove il padre era funzionario delle Ferrovie. Si trasferì con la famiglia a Milano nel 1870. Frequentò dal 1882 l'Accad...

Fueron 32 equipos los que compitieron en la Copa Mundial de Fútbol de 2014, con una plaza destinada al país organizador, Brasil. En el proceso de clasificación para la Copa Mundial de Fútbol de 2014, los equipos inscriptos por las seis confederaciones de la FIFA compitieron por las 31 plazas restantes. En total, participaron en la fase clasificatoria 203 de las 208 asociaciones nacionales afiliadas a FIFA, pues las selecciones de Brunéi, Bután, Guam y Mauritania decidieron no tomar part...

Abolfazl JaliliLahir28 Juni 1957 (umur 67)Saveh, IranKebangsaanIranPekerjaanSutradaraTahun aktifca 1983–sekarang Abolfazl Jalili (Persia: ابوالفضل جلیلی; lahir 28 Juni 1957) adalah seorang sutradara yang berasal dari Iran. Pranala luar Abolfazl Jalili di IMDb (dalam bahasa Inggris) [1] Diarsipkan 2013-05-10 di Wayback Machine. Artikel bertopik biografi tokoh ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.lbs

Degradation of functioning of the brain Aging of the brain is a process of transformation of the brain in older age, including changes all individuals experience and those of illness (including unrecognised illness). Usually this refers to humans. Since life extension is only pertinent if accompanied by health span extension, and, more importantly, by preserving brain health and cognition, finding rejuvenating approaches that act simultaneously in peripheral tissues and in brain function is a...

لمعانٍ أخرى، طالع باتريك ماير (توضيح). باتريك ماير معلومات شخصية الميلاد 28 مارس 1988 (العمر 36 سنة)فانغن إم آلغوي الطول 1.79 م (5 قدم 10 1⁄2 بوصة) مركز اللعب مهاجم الجنسية ألمانيا معلومات النادي النادي الحالي SV Beuren (لاعب ومدرب) مسيرة الشباب سنوات فريق SV Beuren 00...

1966 book by Paul Sweezy and Paul A. Baran This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (July 2019) (Learn how and when to remove this message) Monopoly Capital: An Essay on the American Economic and Social Order Cover of the 1967 editionAuthorsPaul Sweezy, Paul A. BaranLanguageEnglishSubjectMonopolyPublisherMonthly Review...

Vincentian actor (1933–2014) Nik Zaranin The Champions: Desert Journey (1969)BornTracy Connell(1933-01-19)19 January 1933Kingstown, Saint Vincent and the GrenadinesDied3 January 2014(2014-01-03) (aged 80)Kingstown, Saint Vincent and the GrenadinesOccupation(s)Actor, dancer, theatre pioneer, restaurateurYears active1961–1975SpouseToni Tracy Connell (19 January 1933 – 3 January 2014), also known by his stage name Nik Zaran, was a Vincentian actor. Initially a keen sportsman, he ...































