Trapdoor function
|
Read other articles:

Noiron-sous-Gevrey Noiron-sous-Gevrey (Frankreich) Staat Frankreich Region Bourgogne-Franche-Comté Département (Nr.) Côte-d’Or (21) Arrondissement Beaune Kanton Nuits-Saint-Georges Gemeindeverband Gevrey-Chambertin et de Nuits-Saint-Georges Koordinaten 47° 12′ N, 5° 5′ O47.1944444444445.0808333333333Koordinaten: 47° 12′ N, 5° 5′ O Höhe 195–227 m Fläche 6,56 km² Einwohner 1.150 (1. Januar 2020) Bevölkerungsdichte 175 ...

Hafner Rotachute Typ Experimentalflugzeug, Tragschrauber Entwurfsland Vereinigtes Konigreich Vereinigtes Königreich Hersteller F. Hills & Son Erstflug 11. Februar 1942 (im Fahrzeugschlepp) Stückzahl etwa 8 P-5 im Museum of Army Flying Der Hafner Rotachute ist ein als Tragschrauber ausgelegtes experimentelles Fluggerät, das von Raoul Hafner konstruiert und von Hills & Son in Manchester gebaut wurde. Inhaltsverzeichnis 1 Geschichte 1.1 Entwicklung 1.2 Erprobung 1.3 Weitere Nutzu...

Lluvia, vapor y velocidad. El gran ferrocarril del Oeste(Rain, Steam, and Speed –The Great Western Railway) Año 1844Autor Joseph Mallord William TurnerTécnica Óleo sobre lienzoEstilo RomanticismoTamaño 91 cm × 121,8 cmLocalización National Gallery, Londres, Reino Unido Reino Unido[editar datos en Wikidata] Lluvia, vapor y velocidad. El gran ferrocarril del Oeste (en inglés, Rain, Steam, and Speed – The Great Western Railway) es un conocido cuadro del pintor romántic...

In 2003 werd het 89ste Campeonato Paranaense gespeeld voor voetbalclubs uit de Braziliaanse staat Paraná. De competitie werd gespeeld van 25 januari tot 23 maart en werd georganiseerd door de Federação Paranaense de Futebol. Coritiba werd kampioen. Eerste fase De 8 clubs met de beste resultaten gecombineerd over beide groepen stootten door naar de knock-outfase, de twee clubs met de laagste punten degraderen. Groep 1 Plaats Club Wed. W G V Saldo Ptn. 1. Coritiba 8 7 1 0 20:6 15 2. Grêmio ...

2001 single by Nelly Furtado Shit on the Radio redirects here. For the song by Robbie Williams, see Take the Crown. Shit on the Radio (Remember the Days)Standard international artworkSingle by Nelly Furtadofrom the album Whoa, Nelly! ReleasedDecember 3, 2001 (2001-12-03)Studio The Gymnasium (Toronto, Canada) Can-Am Recorders (Tarzana, Los Angeles) Length3:55LabelDreamWorksSongwriter(s)Nelly FurtadoProducer(s) Gerald Eaton Brian West Nelly Furtado Nelly Furtado singles chronolog...
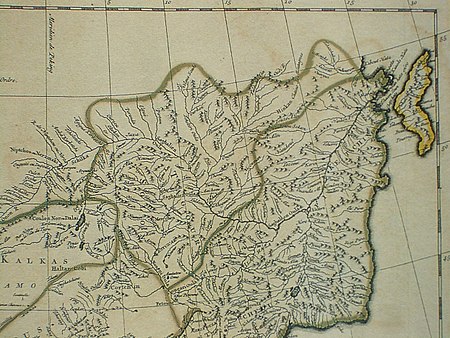
The Solon people (simplified Chinese: 索伦; traditional Chinese: 索倫; pinyin: Suǒlún) are a subgroup of the Ewenki (Evenk) people of northeastern Asia. They live in China's Inner Mongolia Autonomous Region and Heilongjiang Province, and constitute the majority of China's Ewenki. Terminology and classification The lands of the Daur (Tagour) and Solon people shown east and west of the Nonni River on an early 18th-century Jesuit map The Ewenki (also spelled Evenki) people are ...

كلايف أوين معلومات شخصية الميلاد 3 أكتوبر 1964 (العمر 59 سنة)كوفنتري، إنجلترا الإقامة هايغيت مواطنة المملكة المتحدة الزوجة ساره جين 1995-الآن (طفلان) عدد الأولاد 2 الحياة العملية المدرسة الأم الأكاديمية الملكية للفنون المسرحية (التخصص:تمثيل) (–1986) المهنة ممثل أفلام...

American singer (born 1944) This article is about the American singer. For the English children's author, see Diana Ross (author). Diana RossRoss performing in 2022Born (1944-03-26) March 26, 1944 (age 79)Detroit, Michigan, U.S.OccupationsSingeractressYears active1959–present[1]Spouses Robert Ellis Silberstein (m. 1971; div. 1977) Arne Næss Jr. (m. 1986; div. 2000) Chil...

Public park in Beckenham This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Croydon Road Recreation Ground – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Information board by main entrance Croydon Road Recreation Ground is a public park located...

American politician Curtis S. BrambleBramble in July 2014Member of the Utah SenateIncumbentAssumed office January 1, 2001Preceded byHoward C. NielsonConstituency16th district (2001–2023)24th district (2023–present) Personal detailsBornChicago, IllinoisPolitical partyRepublicanSpouseSusanChildren6ResidenceProvoAlma materBrigham Young University (BS, MS)OccupationCertified Public AccountantWebsiteLegislative Website Curtis Scott Bramble is an American politician and Certified Public Acc...

لمعانٍ أخرى، طالع زيد (توضيح). زيد (بالروسية: Антон Заславский) معلومات شخصية اسم الولادة أنتون زاسلافسكي الميلاد 2 سبتمبر 1989 (العمر 34 سنة)ساراتوف الإقامة كايزرسلاوترنلوس أنجلوس (2014–)[1][2] الجنسية ألمانيا العشير سيلينا غوميز (2015–2015)[3]أليسيا ...

Coordenadas: 32° N 80° E Ngariམངའ་རིས་ས་ཁུལ་mnga' ris sa khul阿里地区阿里地區Ālǐ Dìqū Prefeitura Gompa de Chiu, situada perto do lago Manasarovar, com o monte Kailash ao fundo Gompa de Chiu, situada perto do lago Manasarovar, com o monte Kailash ao fundo Localização Mapa do Tibete (a laranja) com a prefeitura de Ngari a vermelhoMapa do Tibete (a laranja) com a prefeitura de Ngari a vermelho Localização em map...

American radio series A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (October 2016) (Learn how and when to remove this template message) Image of trademarked Radio Tales logo and photo of composer Winifred Phillips and producer Winnie Waldron in the Hilton Hotel in New York City after winning a Gracie award i...

У Вікіпедії є статті про інші значення цього терміна: Занзібар. Занзібар суах. Jamhuri ya Watu wa Zanzibar араб. زنجبار Прапор Занзібару Столиця Занзібар Країна Танзанія Підрозділи 5 областей і столиця Офіційна мова англійська і суахілі Населення - повне 1096381[1](2009) Етні...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: St Michael's on Wyre – news · newspapers · books · scholar · JSTOR (July 2007) (Learn how and when to remove this template message) Human settlement in EnglandSt Michael's on WyreSt Michael's Church, St Michael's on WyreSt Michael's on WyreShown within Wyre Bor...
Drupal Тип система управления содержимым Автор Дрис Бёйтарт Разработчик Дрис Бёйтарт и Drupal Association[d] Написана на PHP, с использованием Symfony Операционная система Linux, Windows, macOS и UNIX Первый выпуск 15 января 2001 Последняя версия 10.2.0-rc1[1], &#...

赫尔曼·切尔诺夫赫尔曼·切尔诺夫于2015年10月6日在纽约演讲出生 (1923-07-01) 1923年7月1日(100歲)美国纽约州纽约市公民权美国母校 纽约市立学院 布朗大学 知名于 切尔诺夫界 切尔诺夫分布 切尔诺夫脸 奖项 院士, 美国文理科学院 (1974) 会员, 美国国家科学院 (1980) 威尔克斯纪念奖 (1987) 院士, 美国数学学会 (2012) 科学生涯研究领域 数学 统计学 物理学 机构 UIUC Stanford MIT Harvard �...

Railway station in Tadami, Fukushima Prefecture, Japan This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Aizu-Yokota Station – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this template message) Aizu-Yokota Station会津横田駅Aizu-Ōshio Station in August 2006General...

United States historic placePrimrose CottageU.S. Historic districtContributing property Primrose Cottage, October 2021Location, Roswell, GeorgiaCoordinates34°01′01″N 84°21′52″W / 34.01701°N 84.36441°W / 34.01701; -84.36441Built1839Built byWillis BallArchitectWillis BallPart ofRoswell Historic District (ID74000682[1])Designated CPMay 2, 1974 Primrose Cottage was the first permanent private home in Roswell, Georgia, United States. The house built...

Peta Komun Odalengo Grande (merah) di Wilayah Alessandria (kuning), Piemonte, Itali.Odalengo GrandeKomun di ItaliNegara ItaliDaerahPiedmontWilayahAlessandriaZon waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST) Odalengo Grande merupakan sebuah komun dan bandar yang terletak di Alessandria di Piedmont dalam kawasan Itali. Rujukan lbsPiedmont · Komun Provinsi Alessandria Acqui Terme Albera Ligure Alessandria Alfiano Natta Alice Bel Colle Alluvioni Cambiò Altavilla Monferra...
























