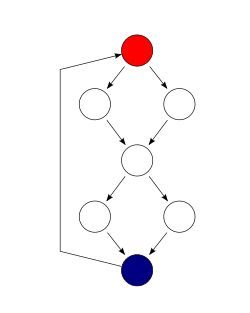
Cyclomatic complexity
|
Read other articles:

IwurDistrikNegara IndonesiaProvinsiPapuaKabupatenPegunungan BintangPemerintahan • Kepala distrik- Osep YikwaPopulasi • Total... jiwa jiwaKode Kemendagri95.02.04 Kode BPS9417010 Luas... km²Kampung/kelurahan... Iwur adalah sebuah distrik di Kabupaten Pegunungan Bintang, Papua, Indonesia. Masyarakat Kampung Digi Dan TNI Indonesia Pembagian administratif Iwur Kurumklin Walapkubun Dinmot Arim Ewenkatop Ulkubi Dipol Nenginum Narnger Kamyoim lbsDistrik Iwur, Kabupaten P...

Artikel ini berisi konten yang ditulis dengan gaya sebuah iklan. Bantulah memperbaiki artikel ini dengan menghapus konten yang dianggap sebagai spam dan pranala luar yang tidak sesuai, dan tambahkan konten ensiklopedis yang ditulis dari sudut pandang netral dan sesuai dengan kebijakan Wikipedia. (Juni 2022) Novotel Suites Yogyakarta MalioboroLokasi di Kota YogyakartaTampilkan peta Kota YogyakartaNovotel Suites Yogyakarta Malioboro (DIY)Tampilkan peta DIYNovotel Suites Yogyakarta Malioboro (Ja...

American politician and judge Joseph PrentisJudge of the General CourtIn officeJanuary 4, 1788 – June 18th, 18096th Speaker of the Virginia House of DelegatesIn officeOctober 16, 1786 – January 8, 1788Preceded byBenjamin Harrison Jr.Succeeded byThomas MatthewsMember of the Virginia House of Delegatesfrom York CountyIn office1777–1778In office1782–1788Member of the Virginia House of Delegatesfrom James City CountyIn office1781–1782Member of the Virginia House of...

Pour les articles homonymes, voir HP Inc. et Hewlett Packard Enterprise. Ne doit pas être confondu avec HP. Hewlett-Packard Company Logo Hewlett-Packard Siège social à Palo Alto en Californie Création 1er janvier 1939 Disparition 31 octobre 2015[1] Fondateurs William HewlettDavid Packard Forme juridique Société anonyme Action New York Stock Exchange (HPQ) et bourse de Tokyo Siège social Palo Alto États-Unis Activité Informatique, périphériques, logiciels, Serveurs, Réseaux P...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Kejatuhan SoehartoBagian dari Reformasi Indonesia Searah jarum jam, dari atas: Presiden Indonesia Soeharto menyampaikan pengunduran diri dari jabatannya Para perusuh membakar perabot kantor di jalan-jalan Jakarta Mahasiswa memprotes pemerintah Mahasiswa Universitas Trisakti dan polisi pada bentrok Tanggal4–21 Mei 1998LokasiIndonesiaHasilKejatuhan Orde Baru Presiden Soeharto mengundurkan diri Peresmian B.J. Habibie sebagai presiden Pembentukan Kabinet Reformasi Pembangunan Referendum kemerde...

Outflow channel on Mars Athabasca VallesThe Athabasca Valles, showing the flow direction of what are interpreted by some researchers to be floodwater-related morphologies. Note streamlined islands which show direction of flow to southwest.Coordinates8°36′N 205°00′W / 8.6°N 205.0°W / 8.6; -205.0Length285.0 km (177.1 mi)NamingRiver in Canada. (Changed from Athabasca Vallis.) The Athabasca Valles are a late Amazonian-period outflow channel system in the central El...

Questa voce o sezione sull'argomento scrittori tedeschi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Jakob Michael Reinhold Lenz Jakob Michael Reinhold Lenz (Cēsvaine, 23 gennaio 1751 – Mosca, 4 giugno 1792) è stato uno scrittore tedesco, uno dei maggiori rappresentanti dello Sturm und Drang. Indice 1 Biografia 1.1 Principali opere 2 Fonti 3 Note ...

A stretch of B C Road Ballygunge Circular Road which was renamed as Promotesh Barua Sarani (PIN Kolkata 700019), after the legendary actor and doyen of Bengali Cinema, is one of the most important roads which runs through the upscale part of Ballygunge in South Kolkata.[1] It starts near the Ballygunge Science College right off Gariahat Road, passing through landmarks like Tripura House, St Lawrence High School etc. before meeting Gurusaday Dutta Road about a mile up the road. It the...

American animated television series Cattanooga CatsGenreComedyWritten byNeal BarberaLarz BourneMike MalteseDirected byWilliam HannaJoseph BarberaVoices ofJim BeggJulie BennettDaws ButlerWilliam CallawayDick CurtisMarty IngelsCasey KasemPaul LyndeAllan MelvinDon MessickJanet WaldoBruce WatsonCountry of originUnited StatesNo. of seasons2No. of episodes17ProductionProducersWilliam HannaJoseph BarberaRunning time60 minutesProduction companyA Hanna-Barbera ProductionOriginal releaseNetworkABCRelea...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

Doro PeschDoro Pesch al Wacken Open Air 2017 Nazionalità Germania GenereHeavy metalHard rock Periodo di attività musicale1983 – in attività Gruppi attualiDoro Gruppi precedentiWarlock Sito ufficiale Modifica dati su Wikidata · Manuale Dorothee Pesch (Düsseldorf, 3 giugno 1964) è una cantante tedesca, heavy metal, membro di gruppi quali Warlock e Doro. È una delle più note voci femminili nella scena heavy metal degli anni ottanta, periodo in cui dominavan...

Questa voce o sezione deve essere rivista e aggiornata appena possibile. Commento: Dal 2013 ha fatto alcune presenze da professionista (vedi sito NFL), ma qui ne sono riportate ancora 0. Sembra infatti che questa voce contenga informazioni superate e/o obsolete. Se puoi, contribuisci ad aggiornarla. Tori Gurley Nazionalità Stati Uniti Altezza 193 cm Peso 105 kg Football americano Ruolo Wide receiver Squadra Cleveland Browns CarrieraGiovanili South Carolina GamecocksSquadre...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2020) يجب على المرء أن يميز مفاهيمياً بين الأنبياء بمعنى الكتب النبوية والأفراد الذين يطلق عليهم الأنبياء. تتضمن...

Not to be confused with Army of the Holy War. Jaysh al-Jihadجيش الجهادLogo of the groupFlag used by the groupLeadersAbu Mussab Al-FanussyDates of operationFebruary 2015[1] – 21 May 2016HeadquartersAl-Qahtaniyah, Quneitra[1]Active regionsQuneitra Governorate and Daraa Governorate, Syria[1]IdeologySalafi JihadismSize500[1]Part of Islamic State (allegedly)AlliesYarmouk Martyrs BrigadeOpponents Syrian Armed Forces National Defense Force Ahrar ash-Sh...

اضغط هنا للاطلاع على كيفية قراءة التصنيف ضفدع نيفادا أصفر الأقدام حالة الحفظ أنواع مهددة بالانقراض (خطر انقراض أدنى) [1] المرتبة التصنيفية نوع التصنيف العلمي النطاق: حقيقيات النوى المملكة: حيوانات الشعبة: الحبليات الشعيبة: الفقاريات العمارة: الرباعية الأطراف ال...

Form of right-wing politics that emerged in the 1960s For specific entities called New Right, see New Right (disambiguation). Not to be confused with Alt-lite. Part of the Politics seriesParty politics Political spectrum Left-wing Far-leftCentre-left Centre Centre-leftRadical centreCentre-right Right-wing Centre-rightFar-right Platforms/Ideologies Anarchist Christian Democratic Communist Conservative Democratic Environmentalist Fascist Fundamentalist Globalist Green Internationalist Liberal L...

Book by George Santayana Scepticism and Animal Faith Dustjacket of the first editionAuthorGeorge SantayanaLanguageEnglishSubjectEpistemologyPublication date1923Media typePrintPages314 (Dover Books edition)ISBN0-486-20236-4 (Dover Books edition) Scepticism and Animal Faith (1923) is a later work by Spanish-born American philosopher George Santayana. He intended it to be merely the introduction to a new system of philosophy, a work that would later be called The Realms of Being, which cons...
Long Island Rail Road station in New York Long Island CityLooking west at the station (to the right of the fence) and yard (to the left); the brick building to the right is ventilation for the Queens–Midtown Tunnel.General informationLocationBorden Avenue and Second Street Hunters Point and Long Island City, Queens, New YorkCoordinates40°44′29″N 73°57′25″W / 40.74139°N 73.95694°W / 40.74139; -73.95694Owned byLong Island Rail RoadLine(s)Main LineMontauk Br...