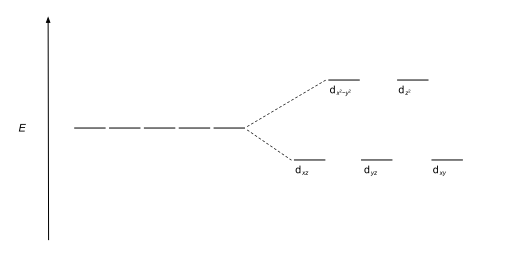
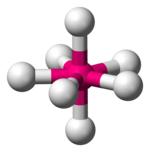
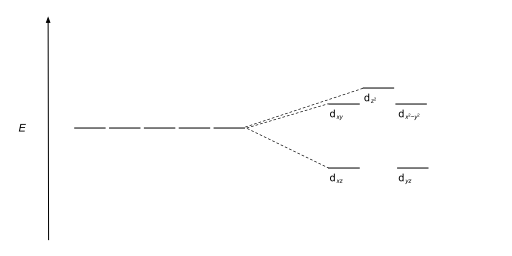
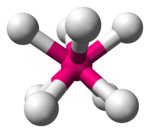
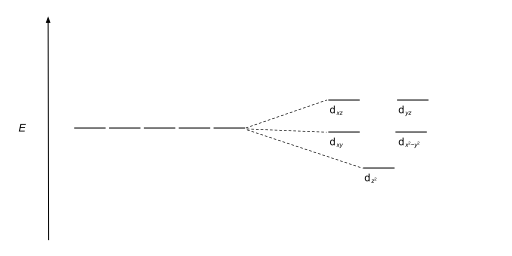
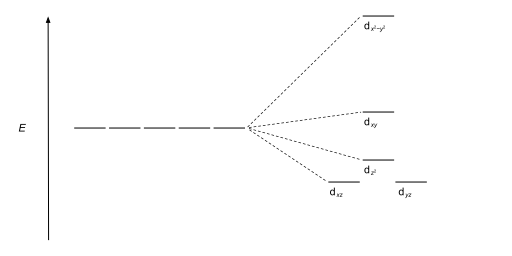
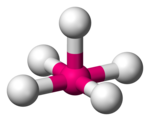
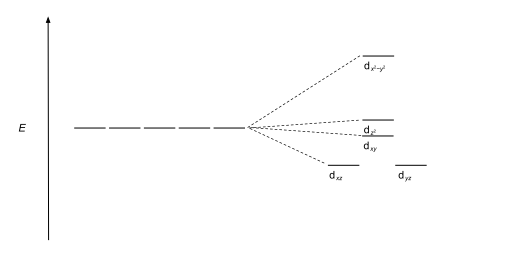
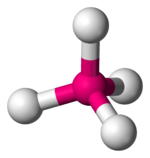
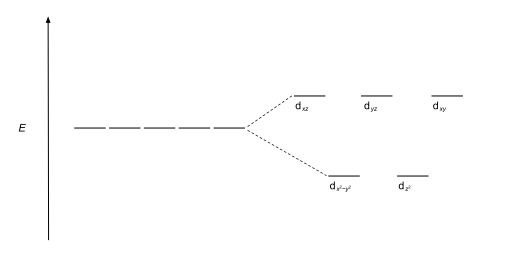
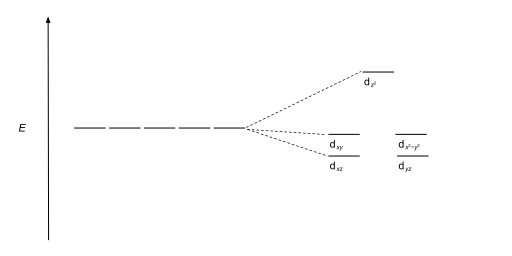
Crystal field theory
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Marcelo Peralta – berita · surat kabar · buku · cendekiawan · JSTOR (March 2020) Marcelo Peralta (5 Maret 1961 – 10 Maret 2020)) adalah pemain musik, guru, komposer, dan arranger dari Argentin...

Golden CrossPoster promosi untuk Golden CrossGenreDrama Balas dendam Romansa ThrillerDitulis olehYoo Hyun-miSutradaraHong Suk-goo[1] Kim Jong-yeonPemeranKim Kang-wooLee Si-youngUm Ki-joonHan Eun-jungNegara asalKorea SelatanBahasa asliKoreaJmlh. episode20ProduksiProduser eksekutifLee Gun-joonLokasi produksiKoreaDurasi70 menit Rabu dan Kamis pukul 22:00 (WSK)Rumah produksiPan EntertainmentDistributorKBSRilis asliJaringanKBSRilis9 April (2014-04-09) –19 Juni 2014 (2014-...

Skema penyepuhan tembaga (Cu) ke suatu permukaan konduktif (Me). Tembaga pada akhirnya akan termakan habis untuk menggantikan ion tembaga yang terdapat di larutan. Penyepuhan[1] atau sepuh listrik (Inggris: electrodepositioncode: en is deprecated ) adalah proses untuk menghasilkan lapisan logam pada permukaan benda padat melalui reaksi redoks menggunakan arus listrik searah. Bagian yang akan dilapisi berperan sebagai katoda atau elektroda negatif dari sel elektrolisis. Elektrolit adal...

Pour les articles homonymes, voir Ministère de la Justice. Ministère japonais de la Justice (ja)法務省HistoireFondation 15 février 1948Prédécesseur Attorney General's Office (d)CadreType Ministère japonaisForme juridique Agence publiqueSiège 1-1-1 Kasumigaseki, Chiyoda, TokyoPays JaponCoordonnées 35° 40′ 35″ N, 139° 45′ 12″ ELangue JaponaisOrganisationEffectif 55 231 employés (31/12/2023)Ministre Ryuji KoizumiBudget 725 044&...

Terrorist attacks in Jakarta, Indonesia 2017 Jakarta bombingsPart of terrorism in Indonesia2017 Jakarta bombings (Jakarta)Show map of Jakarta2017 Jakarta bombings (Indonesia)Show map of IndonesiaAttack site shown on a map of IndonesiaLocationJakarta, IndonesiaCoordinates6°13′45.56″S 106°51′07.38″E / 6.2293222°S 106.8520500°E / -6.2293222; 106.8520500Date24 May 2017; 6 years ago (2017-05-24) 9:00 – 9:05 WIB (UTC+07:00)Attack typeSuicide b...

Bet on ItSingel oleh Zac Efrondari album High School Musical 2Dirilis11 Desember 2007Direkam2007GenrePop remajaDurasi3:18LabelWalt DisneyPencipta Antonina Armato Tim James Produser Armato James Kronologi singel High School Musical Everyday (2007) Bet on It (2007) Now or Never (2008) Bet on It adalah lagu dari Disney Channel Original Movies, High School Musical 2. Lagu ini ditampilkan di soundtrack film dan dibawakan oleh Zac Efron sebagai Troy Bolton. Komposisi Bet on It telah digambarka...

Map of Lower and Upper Egypt Mesir Kuno terbagi atas dua wilayah, yang dikenal sebagai Mesir Hulu dan Mesir Hilir. Di bagian utara adalah Mesir Hilir di mana Sungai Nil berakhir dengan beberapa muaranya dan membentuk Delta Sungai Nil. Di bagian selatan adalah Mesir Hulu, yang membujur sampai ke Syene. Kedua negara, Mesir Atas dan Bawah bersatu pada kira-kira tahun 3100 SM, tetapi masing-masing masih mempertahankan kerajaannya. Firaun merupakan pemimpin kedua kerajaan tersebut. Penamaan Hulu d...

يونيفرسال انتراكتيفيونيفرسال انتراكتيفالشعارمعلومات عامةالبلد الولايات المتحدة التأسيس 1993النوع شركة ألعابالمقر الرئيسي لوس أنجلوس، كاليفورنيا، الولايات المتحدةالمنظومة الاقتصاديةالصناعة الترفيه التفاعلي صناعة ألعاب الفيديوالمنتجات ألعاب الفيديومناطق الخدمة الول...

Radio station in Windsor Locks, ConnecticutWUCSWindsor Locks, ConnecticutBroadcast areaGreater HartfordFrequency97.9 MHz (HD Radio)BrandingFox Sports 97.9ProgrammingFormatSports radioAffiliationsFox Sports RadioNew York Yankees Radio NetworkOwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsWHCN, WKSS, WPOP, WWYZHistoryFirst air dateJuly 1990; 33 years ago (1990-07)[1]Former call signsWPKX (1990–2012)Call sign meaningUniversity of Connecticut—S...

Scientific instrument This article is about microscopes, the instruments, in general. For light microscopes, see Optical microscope. For other uses, see Microscope (disambiguation). This scientific article needs additional citations to secondary or tertiary sources such as review articles, monographs, or textbooks. Please also establish the relevance for any primary research articles cited. Unsourced or poorly sourced material may be challenged and removed. (April 2017) (Learn how and when to...

English poet (1916–2018) The Right HonourableThe Lady Wilson of RievaulxMary Wilson in 1970BornGladys Mary Baldwin(1916-01-12)12 January 1916Diss, EnglandDied6 June 2018(2018-06-06) (aged 102)London, EnglandResting placeSt Mary's Old Church, St Mary's, Isles of ScillyOccupationsPoetstenographerKnown forSpouse of the prime minister of the United Kingdom (1964–1970, 1974–1976)Political partyLabourSpouse Harold Wilson (m. 1940; died&#...

Novel by Nicholas Sparks Not to be confused with The Lucky Ones (book), by Rachel Cusk. The Lucky One First editionAuthorNicholas SparksCountryUnited StatesLanguageEnglishGenreRomanceDramaWarPublisherGrand Central PublishingPublication date2008Media typePrint (hardcover)Pages386 ppISBN0-446-57993-9OCLC233573959Dewey Decimal813/.54 22LC ClassPS3569.P363 L83 2008Preceded byThe Choice The Lucky One is a 2008 romance novel by American writer Nicholas Sparks. U.S. Marine Logan...

Keuskupan Agung AcerenzaArchidioecesis AcheruntinaKatolik Katedral AcerenzaLokasiNegara ItaliaProvinsi gerejawiPotenza-Muro Lucano-Marsico NuovoStatistikLuas1.250 km2 (480 sq mi)Populasi- Total- Katolik(per 2011)42.81542,382 (99%)Paroki21InformasiDenominasiGereja KatolikRitusRitus RomaPendirianAbad ke-4KatedralCattedrale dell’Assunzione della B. Maria VergineKepemimpinan kiniPausFransiskusUskup AgungFrancesco SirufoEmeritusMichele ScandiffioSitus webw...

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1]...

Cencerro. Patrón rítmico típico El cencerro es un instrumento musical de percusión. Modernamente se fabrican pequeñas campanas o cencerros sin badajo específicos para ser usados como instrumentos musicales. Pueden estar fijos a un soporte y son idiófonos sacudidos. Se percuten con baquetas de madera especialmente diseñadas para este instrumento. Normalmente, se fabrican en cobre, acero o en aleación de acero. Se utilizan de distintos tamaños para conseguir diversos sonidos dependien...

Railway station in China This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Guojiaying railway station – news · newspapers · books · scholar · JSTOR (March 2010) (Learn how and when to remove this message) Guojiaying railway station is a station of Jingbao Railway in Inner Mongolia. See also List of stations on Jingbao railway v...

American actor (1904–1972) Bruce CabotCabot in Sinners in Paradise (1938)BornEtienne Pelissier Jacques de Bujac(1904-04-20)April 20, 1904Carlsbad, Territory of New Mexico, U.S.DiedMay 3, 1972(1972-05-03) (aged 68)Woodland Hills, California, U.S.OccupationActorYears active1931–1971Spouses Gracy Mary Mather Smith (m. 1926; div. 1930) Adrienne Ames (m. 1933; div. 1937) France...

Attitudes and behaviors towards sex in ancient Rome Satyr and nymph, mythological symbols of sexuality on a mosaic from a bedroom in Pompeii. Sexual attitudes and behaviors in ancient Rome are indicated by art, literature, and inscriptions, and to a lesser extent by archaeological remains such as erotic artifacts and architecture. It has sometimes been assumed that unlimited sexual license was characteristic of ancient Rome,[1][2] but sexuality was not excluded as a concern of...

У этого термина существуют и другие значения, см. Преображенский. ПосёлокПреображенский 54°22′52″ с. ш. 43°49′41″ в. д.HGЯO Страна Россия Субъект Федерации Мордовия Муниципальный район Краснослободский Сельское поселение Старозубаревское История и география П�...

Matori Abdul Djalil Menteri Pertahanan Indonesia ke-23Masa jabatan10 Agustus 2001 – 20 Oktober 2004PresidenMegawati SoekarnoputriPendahuluAgum GumelarPenggantiJuwono Sudarsono Informasi pribadiLahir(1942-07-11)11 Juli 1942Salatiga, Jawa Tengah, Masa Pendudukan JepangMeninggal12 Mei 2007(2007-05-12) (umur 64)Jakarta, IndonesiaKebangsaanIndonesiaPartai politikPKBPekerjaanPolitisiSunting kotak info • L • B H. Matori Abdul Djalil, S.H. (11 Juli 1942 –&...