Commutator subgroup
|
Read other articles:

British soldier and politician (1724–1807) The Most HonorableThe Marquess TownshendPCPortrait by George RomneyBorn28 February 1724London, EnglandDied14 September 1807 (aged 83)Raynham Hall, NorfolkAllegiance Kingdom of Great BritainService/branch British ArmyYears of service1743–1796RankField MarshalBattles/warsWar of the Austrian SuccessionJacobite RisingSeven Years' War Field Marshal George Townshend, 1st Marquess Townshend, PC (28 February 1724 – 14 Septem...
Leigh dans le Grand Manchester. La circonscription de Leigh est une circonscription électorale anglaise située dans le Grand Manchester et représentée à la Chambre des Communes du Parlement britannique. Résultats électoraux Élections générales britanniques de 2019 — Leigh[1] Élections générales britanniques de 2019 Nom Parti politique Voix % ±% Maj. James Grundy Conservateur 21 266 45,27 % 9,4 1 965 Jo Platt (sortant) Travailliste 19 301 41,08 % −15,...

Constantin VIII Empereur byzantin Constantin VIII Règne Co-empereur : 962 - 15 décembre 1025 Empereur : 15 décembre 1025 - 11 novembre 1028 2 ans, 10 mois et 27 jours Période Macédonienne Précédé par Basile II Co-empereur Romain II (962-963) Basile II (962-1025) Nicéphore II Phocas (963-969) Jean Ier Tzimiskès (969-976) Suivi de Zoé Porphyrogénète Romain III Argyre Biographie Naissance vers 960 (probablement Didymotique ou Constantinople) Décès 11 nove...

American television game show This article is about the American game show. For other uses, see Joker's Wild (disambiguation). The Joker's WildAlso known asJoker! Joker!! Joker!!!Created byJack BarryDirected byRichard S. Kline[1]D.A. DianaRich DiPirroPresented byJack BarryBill CullenPat FinnSnoop DoggNarrated byJohnny JacobsJay StewartCharlie O'DonnellEd MacKayDave BurchellTheme music composerPerrey and KingsleyHal HideyAlan ThickeJoe Manolakakis[1]Country of originUnited Stat...

Pour les articles homonymes, voir ENSTA (homonymie). École nationale supérieure de techniques avancéesHistoireFondation 1741StatutType École d'ingénieurs et EPSCP-GEForme juridique Établissement public national à caractère scientifique culturel et professionnel (d)Nom officiel ENSTA ParisRégime linguistique FrançaisFondateur Henri Louis Duhamel du MonceauPrésident Laurent Giovachini (depuis 2020)Directeur Élisabeth CréponMembre de Institut Polytechnique de Paris, CGE, CDEFI, Pro...

Italian football club Football clubA.C.D. Castel di Sangro Cep 1953Full nameAssociazione Calcistica Dilettantistica Castel di Sangro Cep 1953Nickname(s)Giallorossi (Yellow-reds), Sangrini, Castello (Castle), CastelsangroFounded19532005 (refounded)2012 (refounded)GroundStadio Teofilo Patini,Castel di Sangro, ItalyCapacity7,220ChairmanGiuseppe SantostefanoManagerDomenico CristianoLeagueEccellenza Molise2020–21Eccellenza Molise, 7th Home colours Away colours Castel di Sangro Cep is an Italian ...
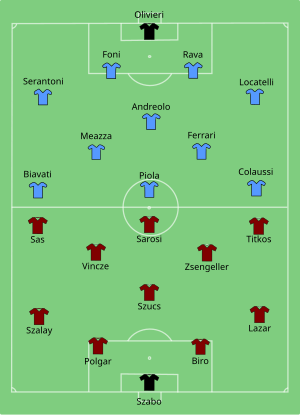
Overview of Hungary at the FIFA World Cup Hungary lining up for their semi-final match against Uruguay at the 1954 FIFA World Cup in Lausanne. The FIFA World Cup is an international association football competition contested by the men's national teams of the members of Fédération Internationale de Football Association (FIFA), the sport's global governing body. The championship has been awarded every four years since the first tournament in 1930, except in 1942 and 1946, due to World War II...

Radio station in Hammond, IndianaWJOBHammond, IndianaBroadcast areaChicago metropolitan areaFrequency1230 kHzBrandingAM-1230 WJOBProgrammingFormatTalk - Brokered programmingAffiliationsPremiere NetworksRegional Radio Sports NetworkOwnershipOwnerVazquez Development, LLCHistoryFirst air date1923Former call signsWWAE (1923-1940)Technical information[1]Licensing authorityFCCFacility ID12219ClassC (AM)D (FM)Power1,000 wattsERP250 watts (FM)HAAT119 meters (390 ft) (FM)Transmitter coord...

Cypriot singer-songwriter Alexia VassiliouBorn (1964-02-05) 5 February 1964 (age 60)Famagusta, CyprusNationalityCyprusEducationBerklee College of MusicOccupationsingerKnown for40 years of entertaining including twice at Eurovision Alexia Vassiliou (Greek: Αλεξία Βασιλείου; born 5 February 1964) is a Cypriot singer-songwriter. She has represented her country in the Eurovision contest in 1981 and 1987. She became a refugee at age ten and still gives concerts for the Uni...

Ilmari Nurminen Ilmari Nurminen 2016. Ledamot av Finlands riksdag Innehar befattningen Tillträdde befattningen 2015 Valkrets Birkaland Född 24 februari 1991 (33 år)Vammala Politiskt parti Socialdemokraterna Webbplats http://ilmarinurminen.fi/ Ilmari Taisto Nurminen, född 24 februari 1991 i Vammala, är en finländsk socialdemokratisk politiker. Han är ledamot av Finlands riksdag sedan 2015.[1] Nurminen blev invald i riksdagsvalet 2015 med 5 079 röster från Birkalan...

Interdisciplinary academic field This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (August 2021) Men's studies is an interdisciplinary academic field devoted to topics concerning men, masculinity, gender, culture, politics and sexuality. It academically examines what it means to be a man in contemporary society.[1] Origins This section needs ...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

The Scent of Green PapayaSutradaraTran Anh HungProduserChristophe RossignonDitulis olehTran Anh HungPenata musikTôn-Thât TiêtSinematograferBenoît DelhommePenyuntingNicole DedieuJean-Pierre RoquesDistributorPrésident FilmsTanggal rilis8 Juni 1993Durasi104 menitNegaraPrancisBahasaVietnamPendapatankotor$1,700,992[1] The Scent of Green Papaya (Vietnam: Mùi đu đủ xanh, Prancis: L'Odeur de la papaye verte) merupakan suatu film berbahasa Vietnam 1993 yang diproduksi di Pranci...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Songs of Europe 1981 concert – news · newspapers · books · scholar · JSTOR (August 2012) (Learn how and when to remove this message) Songs of EuropeDatesAir date22 August 1981HostVenueMomarken, Mysen, NorwayPresenter(s)Rolf KirkvaagTitten TeiMusical direct...

County-like political entities in Quebec, Canada For a list of Quebec's regional county municipalities, see List of regional county municipalities and equivalent territories in Quebec. Not to be confused with county-level city, county, county municipality, regional municipality, rural municipality, or local government.Regional county municipalities of QuebecAlso known as:Municipalités régionales de comté du QuébecLocationProvince of QuebecNumber87Populations7,082 (L'Île-d'Orléans) – 1...

لحدادشة تقسيم إداري البلد المغرب الجهة الرباط سلا القنيطرة الإقليم سيدي قاسم الدائرة تلال الغرب الجماعة القروية سيدي أحمد بنعيسى المشيخة سيدي قاسم بن جميل السكان التعداد السكاني 135 نسمة (إحصاء 2004) • عدد الأسر 19 معلومات أخرى التوقيت ت ع م±00:00 (توقيت قياسي)[1]، �...

Church in Woodrow Road at Bishop Eddie L. Long Parkway Stonecrest, United StatesNew Birth Missionary Baptist ChurchNew Birth MBC in 2017Location6400 Woodrow Road at Bishop Eddie L. Long Parkway StonecrestCountry United StatesMembership10,000Websitenewbirth.orgHistoryFounded(1939); 1983ClergySenior pastor(s)Eddie Long (1987 - 2017) Jamal Harrison Bryant New Birth Missionary Baptist Church is a charismatic Christian Baptist megachurch in Stonecrest, DeKalb County, Georgia. Its senior past...

Disused railway station in Abermule, Powys AbermuleAbermule railway station in 1953General informationLocationAbermule, PowysWalesPlatforms3Other informationStatusDisusedHistoryOriginal companyOswestry and Newtown RailwayPre-groupingCambrian RailwaysPost-groupingGreat Western RailwayKey dates14 August 1860[1]Opened14 June 1965[1]Closed Remains of the station in 1994 Abermule railway station served the village of Abermule (Abermiwl in Welsh) in Wales. Served by the Oswestry and...

Cinema in the UK BFI Southbank BFI Southbank (from 1951 to 2007, known as the National Film Theatre) is the leading repertory cinema in the UK, specialising in seasons of classic, independent and non-English language films. It is operated by the British Film Institute. Forbes called its largest cinema, NFT1, one of the crown jewels of the London film scene.[1] History Old NFT logo The National Film Theatre was initially opened in a temporary building (the Telecinema) at the Festival o...

Bataille de Ligny La bataille de Ligny par Ernest Crofts. Informations générales Date 16 juin 1815 Lieu Ligny (Belgique) Issue Victoire française Belligérants Empire français Royaume de Prusse Commandants Napoléon Ier Gebhard von Blücher Forces en présence 3 corps d'armée (moins de 60 000 hommes) 90 000 à 95 000 hommes Pertes 8 000-12 000 tués ou blessés 12 000 tués ou blessés 8 000 déserteurs Campagne des Cent-JoursS...





![{\displaystyle [g,h]=g^{-1}h^{-1}gh}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e87495055902ee8caee67b2645802bd3192d68c5)
![{\displaystyle [g,h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f333f57962c0c7a4f1f9caa3c965a48437d8544)

![{\displaystyle gh=hg[g,h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd56cfe6eaeab5a364a1f4a39ad6090b6fee18a2)
![{\displaystyle [g,h]=ghg^{-1}h^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1961e7629b74db72c10639ec6f71fdf70a4c6163)
![{\displaystyle gh\neq hg[g,h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/399fa5e528e2a5968aa7399567aa950cd32bf160)
![{\displaystyle gh=[g,h]hg}](https://wikimedia.org/api/rest_v1/media/math/render/svg/995a960c8f521e5543abd39a0cbaae4300edc196)
![{\displaystyle [g,h]^{-1}=[h,g],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcd81f083f7c30aa1e16c041658e6f5c5b9a5750)
![{\displaystyle [g,h]^{s}=[g^{s},h^{s}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f38ed06e15e18efbfe86c7633e9c625b659c00fd)




![{\displaystyle f([g,h])=[f(g),f(h)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73d20d1a1e5883690634a6c57fc1ad64b3b194d1)

![{\displaystyle [G,G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ddf7a724a331d1e12ffa6571ba246ebf08f1335)


![{\displaystyle [g_{1},h_{1}]\cdots [g_{n},h_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9c06725986ed3b3c12d7464b4fd4aa9ca519985)

![{\displaystyle ([g_{1},h_{1}]\cdots [g_{n},h_{n}])^{s}=[g_{1}^{s},h_{1}^{s}]\cdots [g_{n}^{s},h_{n}^{s}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30bd70d0cc28f0dd14964308e01565a77ae93a88)
![{\displaystyle f([g_{1},h_{1}]\cdots [g_{n},h_{n}])=[f(g_{1}),f(h_{1})]\cdots [f(g_{n}),f(h_{n})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/395f7030b9ea3e6fb2efa1954cd2bcbd6970fcb8)
![{\displaystyle f([G,G])\subseteq [H,H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dda17f00885eb853f5fbe77a4f478d561bd80e42)

![{\displaystyle G^{(n)}:=[G^{(n-1)},G^{(n-1)}]\quad n\in \mathbf {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/52ef2cb916cce0b357a95ee734be242ea1a3d737)


![{\displaystyle G_{n}:=[G_{n-1},G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45b52513a2ec52c658b2630a3209588d71cd440e)
![{\displaystyle [G,G]\subseteq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c2fbaaa4367d77150cf65adf348b6c8608489aa)
![{\displaystyle G/[G,G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/169489000a5a3370a8d0a56d35924011e53b6ab1)







![{\displaystyle G\to G/[G,G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceead0a94124820b8210a7c92498bffcb1f7d165)









